Как правильно зажать распределение Бекмана

Question

Я пытаюсь реализовать модель затенения Microfacet BRDF (похожую на модель Кука-Торранса), и у меня возникают некоторые проблемы с распределением Бекмана, определенным в этом документе: https://www.cs.cornell.edu/~srm/publications/EGSR07-btdf.pdf

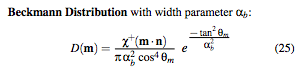
Где M - нормаль в микроснимке, N - нормаль в макроскопе, а ab - параметр "твердости" между [0, 1].

Моя проблема в том, что это распределение часто возвращает непристойно большие значения, особенно когда ab очень мало.

Например, распределение Бекмана используется для расчета вероятности генерации нормального микрофаска M по этому уравнению:

Вероятность должна быть в диапазоне [0,1], так как можно получить значение в этом диапазоне, используя функцию выше, если распределение Бекмана дает мне значения размером 1000000000+?

Так есть ли правильный способ зажать распределение? Или я неправильно понимаю это или функцию вероятности? Я пытался просто ограничить его до 1, если значение превысило 1, но это не дало мне результатов, которые я искал.

Answer 1

У меня был тот же вопрос, что и вы.

Если вы читаете

http://blog.selfshadow.com/publications/s2012-shading-course/hoffman/s2012_pbs_physics_math_notes.pdf

а также

http://blog.selfshadow.com/publications/s2012-shading-course/hoffman/s2012_pbs_physics_math_notebook.pdf

Вы заметите, что это совершенно нормально. Цитировать по ссылкам:

"Параметр ckb Бекмана равен среднеквадратичному наклону (среднеквадратичному) наклона. Поэтому его допустимый диапазон составляет от 0 (без учета –0 соответствует идеальному зеркалу или дельте Дирака и вызывает деление на 0 ошибок в формулировке Бекмана) и до сколь угодно высоких значений. Для значения 1 нет особого значения - это просто означает, что среднеквадратичное отклонение составляет 1/1 или 45°.(...)"

Также другая цитата:

"Статистическое распределение ориентаций в микрообъектах определяется через функцию нормального распределения в микрообъектах D(m). В отличие от F (), значение D() не ограничивается значением от 0 до 1, хотя значения должны быть неотрицательными, они может быть сколь угодно большим (что указывает на очень высокую концентрацию микрообъектов с нормалями, указывающими в определенном направлении). (...)"

Вы должны поискать в Google курсы по физическому шейдингу Self Shadow, в которых много полезного материала (для каждого года есть одно сообщение в блоге: 2010, 2011, 2012 и 2013)