quadprog не может найти решение
Я пытаюсь оптимизировать расположение набора ящиков по месту их вешалки, чтобы ящики были максимально выровнены со своими вешалками и не вытесняли друг друга. Использование quadprog.
Гивенс:
1. box hanger x-locations (P). =710 850 990 1130
2. box-sizes (W). =690 550 690 130
3. usable x-spread tuple (S). =-150 2090
4. number of boxes (K). =4
5. minimum interbox spread (G). =50
6. box x-locations (X). =objective
Мы можем видеть, что полный требуемый x-разброс равен сумме (W) + 3G = 2060 + 150 = 2210, тогда как доступный x-разброс равен S [2] - S 1 = 2240. Таким образом, решение должно существовать.
Min:
sumof (P[i] – X[i])^2
s.t.:
(1) X [i + i] - X[i] >= G + ½ ( W[i+1] + W[i]); я = 1..(К-1), то есть ящики не вытесняют друг друга
-X[i] + X[i+1] >= -( -G – ½ (W[i+1] + W[i]) )
(2) X 1 > = S [левый] + ½ W 1 и (3) X[K] <= S[правый] - ½ W[K], т. Е. Прямоугольники находятся в заданном x-разбросе
X[1] >= - ( S[left] + ½ W[1] )
-X[K] >= - ( S[right] – ½ W[K] )
всего 5 ограничений - 3 для спреда между боксами и 2 для конечностей.
в R:
> Dmat = matrix(0,4,4)
> diag(Dmat) = 1
> dvec = P, the hanger locations
[1] 710 850 990 1130
> bvec
[1] -670 -670 -460 -195 2025
> t(Amat)
[,1] [,2] [,3] [,4]
[1,] -1 1 0 0
[2,] 0 -1 1 0
[3,] 0 0 -1 1
[4,] 1 0 0 0
[5,] 0 0 0 -1
> solve.QP(Dmat, dvec, Amat, bvec)
Error in solve.QP(Dmat, dvec, Amat, bvec) :
constraints are inconsistent, no solution!
Совершенно очевидно, что я пропустил или неправильно указал проблему ( пакет 'quadprog')! Я использую quadprog, так как я нашел его порт JavaScript.
Большое спасибо.
2 ответа
Я не уверен, что это решит вашу физическую проблему, но приведенный ниже код, похоже, решает проблему оптимизации, как вы ее заявили. Я обобщил его на переменное количество блоков и включил график, чтобы проверить решение.
library(quadprog)
p <- c(710, 850, 990, 1130) # hanger positions
w <- c(690, 550, 690, 130) # box widths
g <- 50 # min box separation
s <- c(-150, 2390) # min and max postions of box edges
k <- length(w) # number of boxes
Dmat <- 2*diag(nrow=k)
dvec <- p
# separation constraints
Amat <- -diag(nrow=k,ncol=(k-1))
Amat[lower.tri(Amat)] <- unlist(lapply((k-1):1, function(n) c(1,numeric(n-1))))
bvec <- sapply(1:(k-1), function(n) g + (w[n+1]+w[n])/2)
# x-spread constraints
Amat <- cbind(Amat, c(1,numeric(k-1)), c(numeric(k-1),-1))
bvec <- c(bvec, s[1] + w[1]/2, -(s[2] - w[k]/2))
sol <- solve.QP(Dmat, dvec, Amat, bvec)
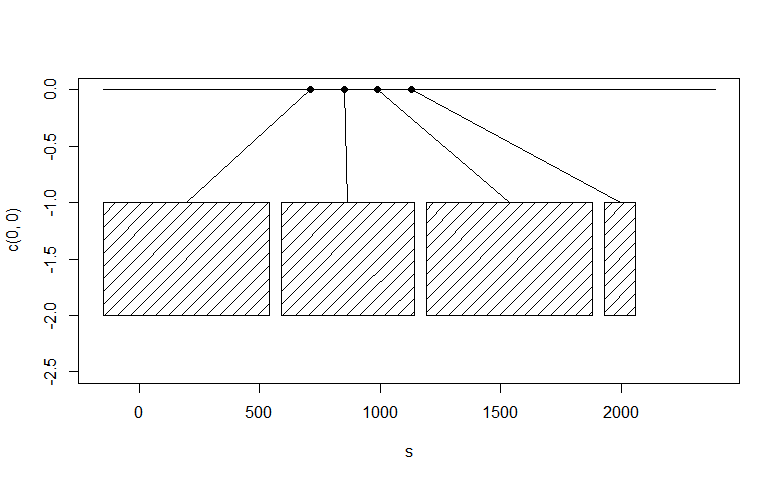
plot(x=s, y=c(0,0), type="l", ylim=c(-2.5,0))
points(x=p, y=numeric(k), pch=19)
segments(x0=sol$solution, y0=-1, x1=p, y1=0)
rect(xleft=sol$solution-w/2, xright=sol$solution+w/2, ytop=-1.0, ybottom=-2, density=8)
Проблема заключается в настройке Amat, bvec или оба. solve.QP пытается найти решение, bзадачи квадратичного программирования при условии ограничения
t(Amat)*b >= bvec
Расширяя это ограничение в вашем примере, мы хотим найти вектор b := c(b[1], b[2], b[3], b[4]) что удовлетворяет условиям:
-b[1] + b[2] >= -670,-b[2] + b[3] >= -670,-b[3] + b[4] >= -460,b[1] >= -195а также
-b[4] >= 2025(То есть,b[4] <= -2025).
Однако, сложив вместе первые четыре неравенства, мы имеем b[4] >= -670-670-460-195 = -1995, Другими словами, b[4] должен быть больше чем -1995 и меньше чем -2025, Это противоречие и, следовательно, solve.QP не может найти решение.
Попытка этого примера с ограничением -b[4] >= -2025, установив bvec = c(-670, -670, -460, -195, -2025) дает решение. Не вдаваясь слишком в вашу формулировку выше, возможно, это было задумано (или другое из этих значений должно было быть положительным)?