Найти углы многоугольника, представленного маской региона
BW = poly2mask(x, y, m, n)вычисляет маску двоичной области интереса (ROI), BW, из многоугольника ROI, представленного векторами x и y. Размер BW м-н-н.
poly2maskустанавливает пиксели в BW, которые находятся внутри многоугольника (X,Y) в 1 и устанавливает пиксели вне многоугольника в 0.
Проблема: учитывая такую двоичную маску BW из выпуклого четырехугольника, что будет наиболее эффективным способом определения четырех углов?
Например,

Лучшее решение на данный момент: использование edge чтобы найти ограничивающие линии, выполните преобразование Хафа, чтобы найти 4 линии на краевом изображении, а затем найдите точки пересечения этих 4 линий или используйте угловой детектор на краевом изображении. Кажется сложным, и я не могу не чувствовать, что есть более простое решение.
Btw, convhull не всегда возвращает 4 балла (может быть, кто-то может предложить qhull варианты, чтобы предотвратить это): он также возвращает несколько точек по краям.
РЕДАКТИРОВАТЬ: ответ Амро кажется довольно элегантным и эффективным. Но в каждом реальном углу может быть несколько "углов", поскольку пики не уникальны. Я мог бы сгруппировать их по θ и усреднить "углы" за реальным углом, но главная проблема - это использование order(1:10),
Является 10 достаточно, чтобы учесть все углы или это исключит "угол" в реальном углу?
5 ответов
Это несколько похоже на то, что предложил @AndyL. Однако я использую граничную сигнатуру в полярных координатах вместо касательной.
Обратите внимание, что я начинаю с выделения краев, получения границы, а затем преобразования ее в подпись. Наконец, мы находим точки на границе, наиболее удаленные от центроида, эти точки составляют найденные углы. (В качестве альтернативы мы также можем обнаружить пики в сигнатуре для углов).
Ниже приведена полная реализация:
I = imread('oxyjj.png');
if ndims(I)==3
I = rgb2gray(I);
end
subplot(221), imshow(I), title('org')
%%# Process Image
%# edge detection
BW = edge(I, 'sobel');
subplot(222), imshow(BW), title('edge')
%# dilation-erosion
se = strel('disk', 2);
BW = imdilate(BW,se);
BW = imerode(BW,se);
subplot(223), imshow(BW), title('dilation-erosion')
%# fill holes
BW = imfill(BW, 'holes');
subplot(224), imshow(BW), title('fill')
%# get boundary
B = bwboundaries(BW, 8, 'noholes');
B = B{1};
%%# boudary signature
%# convert boundary from cartesian to ploar coordinates
objB = bsxfun(@minus, B, mean(B));
[theta, rho] = cart2pol(objB(:,2), objB(:,1));
%# find corners
%#corners = find( diff(diff(rho)>0) < 0 ); %# find peaks
[~,order] = sort(rho, 'descend');
corners = order(1:10);
%# plot boundary signature + corners
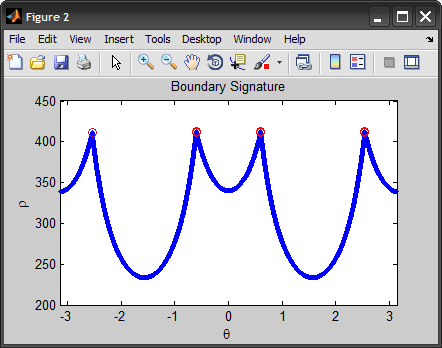
figure, plot(theta, rho, '.'), hold on
plot(theta(corners), rho(corners), 'ro'), hold off
xlim([-pi pi]), title('Boundary Signature'), xlabel('\theta'), ylabel('\rho')
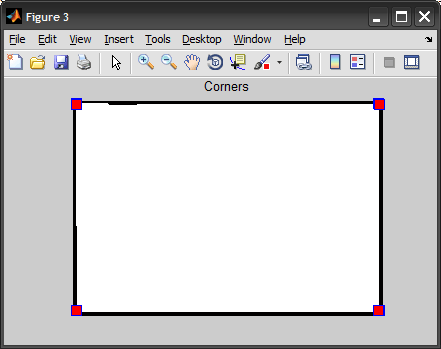
%# plot image + corners
figure, imshow(BW), hold on
plot(B(corners,2), B(corners,1), 's', 'MarkerSize',10, 'MarkerFaceColor','r')
hold off, title('Corners')
РЕДАКТИРОВАТЬ: В ответ на комментарий Джейкоба, я должен объяснить, что я сначала попытался найти пики в сигнатуре, используя первый / второй производные, но в итоге взял самые дальние N-баллов. 10 было просто специальным значением, и его было бы сложно обобщить (я попытался взять 4, равное числу углов, но это не охватывало все из них). Я думаю, что идея кластеризации их для удаления дубликатов стоит рассмотреть.
Насколько я понимаю, проблема с 1-м подходом заключалась в том, что если вы планируете rho без принятия θ во внимание, вы получите другую форму (не те же пики), так как скорость, с которой мы прослеживаем границу, отличается и зависит от кривизны. Если бы мы могли выяснить, как нормализовать этот эффект, мы могли бы получить более точные результаты, используя производные.
Если у вас есть набор инструментов для обработки изображений, есть функция cornermetric который может реализовать детектор угла Харриса или метод минимального собственного значения Ши и Томази. Эта функция присутствует с версии 6.2 панели инструментов обработки изображений (версия MATLAB R2008b).
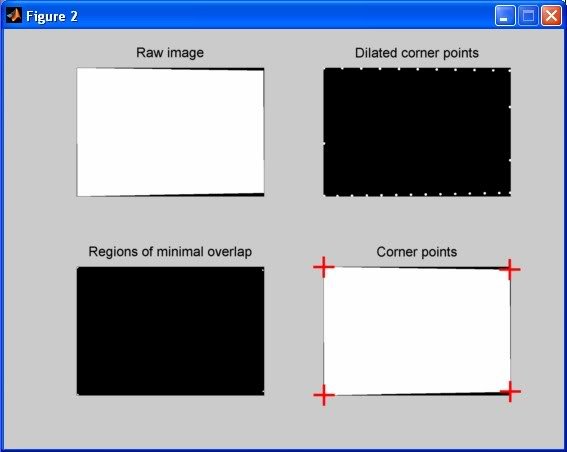
Используя эту функцию, я придумал немного другой подход, чем другие ответы. Приведенное ниже решение основано на идее, что круговая область с центром в каждой "истинной" угловой точке будет перекрывать многоугольник на меньшую величину, чем круговая область с центром в ошибочной угловой точке, которая фактически находится на краю. Это решение также может обрабатывать случаи, когда несколько точек обнаруживаются в одном и том же углу...
Первый шаг - загрузить данные:
rawImage = imread('oxyjj.png');
rawImage = rgb2gray(rawImage(7:473, 9:688, :)); % Remove the gray border
subplot(2, 2, 1);
imshow(rawImage);
title('Raw image');
Затем вычислите угловую метрику, используя cornermetric, Обратите внимание, что я маскирую угловую метрику исходным многоугольником, так что мы ищем угловые точки, которые находятся внутри многоугольника (т.е. пытаемся найти угловые пиксели многоугольника). imregionalmaxЗатем используется для поиска локальных максимумов. Поскольку у вас могут быть кластеры размером более 1 пикселя с одной и той же угловой метрикой, я затем добавляю шум к максимумам и заново вычисляю, так что я получаю только 1 пиксель в каждой максимальной области. Каждая максимальная область затем помечается с помощью bwlabel:
cornerImage = cornermetric(rawImage).*(rawImage > 0);
maxImage = imregionalmax(cornerImage);
noise = rand(nnz(maxImage), 1);
cornerImage(maxImage) = cornerImage(maxImage)+noise;
maxImage = imregionalmax(cornerImage);
labeledImage = bwlabel(maxImage);
Помеченные области затем расширяют (используя imdilate) с дискообразным структурирующим элементом (создан с использованием strel):
diskSize = 5;
dilatedImage = imdilate(labeledImage, strel('disk', diskSize));
subplot(2, 2, 2);
imshow(dilatedImage);
title('Dilated corner points');
Теперь, когда отмеченные угловые области расширены, они будут частично перекрывать исходный многоугольник. Области на краю многоугольника будут перекрываться примерно на 50%, тогда как области, расположенные на углу, будут перекрываться примерно на 25%. Функция regionprops может использоваться для нахождения областей перекрытия для каждой маркированной области, и 4 области, которые имеют наименьшее количество перекрытий, могут, таким образом, рассматриваться как истинные углы:
maskImage = dilatedImage.*(rawImage > 0); % Overlap with the polygon
stats = regionprops(maskImage, 'Area'); % Compute the areas
[sortedValues, index] = sort([stats.Area]); % Sort in ascending order
cornerLabels = index(1:4); % The 4 smallest region labels
maskImage = ismember(maskImage, cornerLabels); % Mask of the 4 smallest regions
subplot(2, 2, 3);
imshow(maskImage);
title('Regions of minimal overlap');
И теперь мы можем получить пиксельные координаты углов, используя find а также ismember:
[r, c] = find(ismember(labeledImage, cornerLabels));
subplot(2, 2, 4);
imshow(rawImage);
hold on;
plot(c, r, 'r+', 'MarkerSize', 16, 'LineWidth', 2);
title('Corner points');
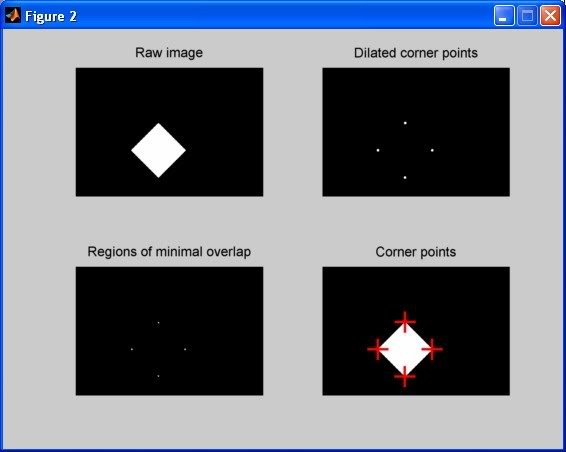
И вот тест с ромбовидной областью:
Мне нравится решать эту проблему, работая с границей, потому что она сводит это от двумерной задачи к одномерной.
использование bwtraceboundary() из инструментария обработки изображений, чтобы извлечь список точек на границе. Затем преобразуйте границу в серию касательных векторов (есть несколько способов сделать это, один из способов состоит в том, чтобы iая точка вдоль границы от i+deltaая точка.) Получив список векторов, возьмите скалярное произведение смежных векторов. Четыре точки с наименьшими точечными произведениями - ваши углы!
Если вы хотите, чтобы ваш алгоритм работал с многоугольниками с неограниченным числом вершин, просто найдите точечные произведения, которые имеют определенное число стандартных отклонений ниже среднего значения.
Я решил использовать угловой детектор Харриса (вот более формальное описание) для получения углов. Это может быть реализовано следующим образом:
%% Constants
Window = 3;
Sigma = 2;
K = 0.05;
nCorners = 4;
%% Derivative masks
dx = [-1 0 1; -1 0 1; -1 0 1];
dy = dx'; %SO code color fix '
%% Find the image gradient
% Mask is the binary image of the quadrilateral
Ix = conv2(double(Mask),dx,'same');
Iy = conv2(double(Mask),dy,'same');
%% Use a gaussian windowing function and compute the rest
Gaussian = fspecial('gaussian',Window,Sigma);
Ix2 = conv2(Ix.^2, Gaussian, 'same');
Iy2 = conv2(Iy.^2, Gaussian, 'same');
Ixy = conv2(Ix.*Iy, Gaussian, 'same');
%% Find the corners
CornerStrength = (Ix2.*Iy2 - Ixy.^2) - K*(Ix2 + Iy2).^2;
[val ind] = sort(CornerStrength(:),'descend');
[Ci Cj] = ind2sub(size(CornerStrength),ind(1:nCorners));
%% Display
imshow(Mask,[]);
hold on;
plot(Cj,Ci,'r*');
Здесь проблема с множественными углами благодаря гауссовой оконной функции, которая сглаживает изменение интенсивности. Ниже приведена увеличенная версия угла с hot Colormap.

Вот пример использования Ruby и HornetsEye. В основном программа создает гистограмму квантованной ориентации градиента Собеля, чтобы найти доминирующие ориентации. Если найдены четыре доминирующие ориентации, линии подгоняются, и пересечения между соседними линиями считаются углами спроецированного прямоугольника.
#!/usr/bin/env ruby
require 'hornetseye'
include Hornetseye
Q = 36
img = MultiArray.load_ubyte 'http://imgur.com/oxyjj.png'
dx, dy = 8, 6
box = [ dx ... 688, dy ... 473 ]
crop = img[ *box ]
crop.show
s0, s1 = crop.sobel( 0 ), crop.sobel( 1 )
mag = Math.sqrt s0 ** 2 + s1 ** 2
mag.normalise.show
arg = Math.atan2 s1, s0
msk = mag >= 500
arg_q = ( ( arg.mask( msk ) / Math::PI + 1 ) * Q / 2 ).to_int % Q
hist = arg_q.hist_weighted Q, mag.mask( msk )
segments = ( hist >= hist.max / 4 ).components
lines = arg_q.map segments
lines.unmask( msk ).normalise.show
if segments.max == 4
pos = MultiArray.scomplex *crop.shape
pos.real = MultiArray.int( *crop.shape ).indgen! % crop.shape[0]
pos.imag = MultiArray.int( *crop.shape ).indgen! / crop.shape[0]
weights = lines.hist( 5 ).major 1.0
centre = lines.hist_weighted( 5, pos.mask( msk ) ) / weights
vector = pos.mask( msk ) - lines.map( centre )
orientation = lines.hist_weighted( 5, vector ** 2 ) ** 0.5
corner = Sequence[ *( 0 ... 4 ).collect do |i|
i1, i2 = i + 1, ( i + 1 ) % 4 + 1
l1, a1, l2, a2 = centre[i1], orientation[i1], centre[i2], orientation[i2]
( l1 * a1.conj * a2 - l2 * a1 * a2.conj -
l1.conj * a1 * a2 + l2.conj * a1 * a2 ) /
( a1.conj * a2 - a1 * a2.conj )
end ]
result = MultiArray.ubytergb( *img.shape ).fill! 128
result[ *box ] = crop
corner.to_a.each do |c|
result[ c.real.to_i + dx - 1 .. c.real.to_i + dx + 1,
c.imag.to_i + dy - 1 .. c.imag.to_i + dy + 1 ] = RGB 255, 0, 0
end
result.show
end