Вычислить момент инерции заданного произвольного выпуклого 2D-многоугольника

Question

Я часами изучал этот вопрос и по какой-то причине не смог найти решение.

Учитывая выпуклый многоугольник, который определяется как массив точек по часовой стрелке вокруг центроида многоугольника, как я могу рассчитать момент инерции многоугольника?

Я смог найти уравнение для различных форм, таких как прямоугольники или круги, но не для произвольного выпуклого многоугольника.

Например, момент инерции прямоугольника, вращающегося вокруг его центроида с массой m, высотой h и шириной w, рассчитывается как:

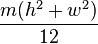
Я ищу похожую формулу / алгоритм, но вместо этого выпуклый многоугольник.

Answer 1

Существует метод анализа двумерного многоугольника с использованием векторной алгебры, который, на мой взгляд, проще реализовать программно, чем методы, основанные на тригонометрии.

Каждый Vector количество состоит из двух компонентов .x а также .y а также методы векторной алгебры векторов, в том числе для точечных и перекрестных произведений

add(a,b) = [a.x+b.x, a.y+b.y]    // a+b = add(a,b)
scale(f,x) = [f*a.x, f*a.y]      // 2*a = scale(2,a), a/3 = scale(1/3,a)
dot(a,b) = a.x*b.x + a.y*b.y     // a·b = dot(a,b)
cross(a,b) = a.x*b.y - a.y*b.x   // a×b = cross(a,b)

Приведенный ниже метод проходит через все стороны многоугольника и суммирует площадь, центр и момент инерции массы относительно начала координат каждого треугольника, определяемого стороной и началом. Окончательная сумма заботится о добавлении или вычитании областей вблизи или вдали от источника и дает точные результаты.

Наконец, момент массы передается от начала координат к центру масс.

polygon(Vector[] points, double depth, double density)
{
    // Accumulate the following values
    double area = 0.0;
    double mass = 0.0;
    Vector center = [0.0, 0.0];
    double mmoi = 0.0;

    // Take each vertex pair starting from the last-first vertex
    // in order to consider all sides.
    int count = points.Length;
    int prev = count - 1;
    for(int index=0; index<count; index++)
    {
        Vector a = points[prev];
        Vector b = points[index];

        double area_step = TriangleArea(a,b);
        double mass_step = density * area_step * depth;
        Vector center_step = TriangleCenter(a,b);
        double mmoi_step = TriangleMmoi(a,b, mass_step);

        area += area_step;
        center = (mass*center + mass_step*center_step)/(mass+mass_step);
        mass += mass_step;
        mmoi += mmoi_step;

        prev = index;
    }

    // Transfer mass moment of inertia from the origin to the center of mass
    mmoi -= mass*dot(center,center);

    // use area, mass, center and mmoi
}

double TriangleArea(Vector a, Vector b)
{
    return cross(a,b)/2;
}
double TriangleCenter(Vector a, Vector b)
{
    return (a+b)/3;
{
double TriangleMmoi(Vector a, Vector b, double triangleMass)
{
    return triangleMass/6*(dot(a,a)+dot(b.b)+dot(a.b));
}

Вышеупомянутый процесс аналогичен описанному в этом ответе. Более подробная информация включена в связанный ответ.

---

Ниже приводится c# реализация вышеуказанного, но с указанием массы, а не плотности и толщины.

public static RigidBody2 FromShape(double mass, params Vector2[] polygon)
{
    double area = 0;
    Vector2 center = Vector2.Zero;
    double mmoi = 0;

    int prev = polygon.Length-1;
    for (int index = 0; index < polygon.Length; index++)
    {
        var a = polygon[prev];
        var b = polygon[index];

        var area_step = Vector2.Cross(a, b)/2;
        var center_step = (a+b)/3;
        var mmoi_step = area_step*(Vector2.Dot(a, a)+Vector2.Dot(b, b)+Vector2.Dot(a, b))/6;

        center = (center*area + center_step * area_step)/(area + area_step);
        area += area_step;
        mmoi += mmoi_step;

        prev = index;
    }

    double density = mass/area;
    mmoi *= density;
    mmoi -= mass * Vector2.Dot(center, center);

    return new RigidBody2(mass, mmoi, center);
}

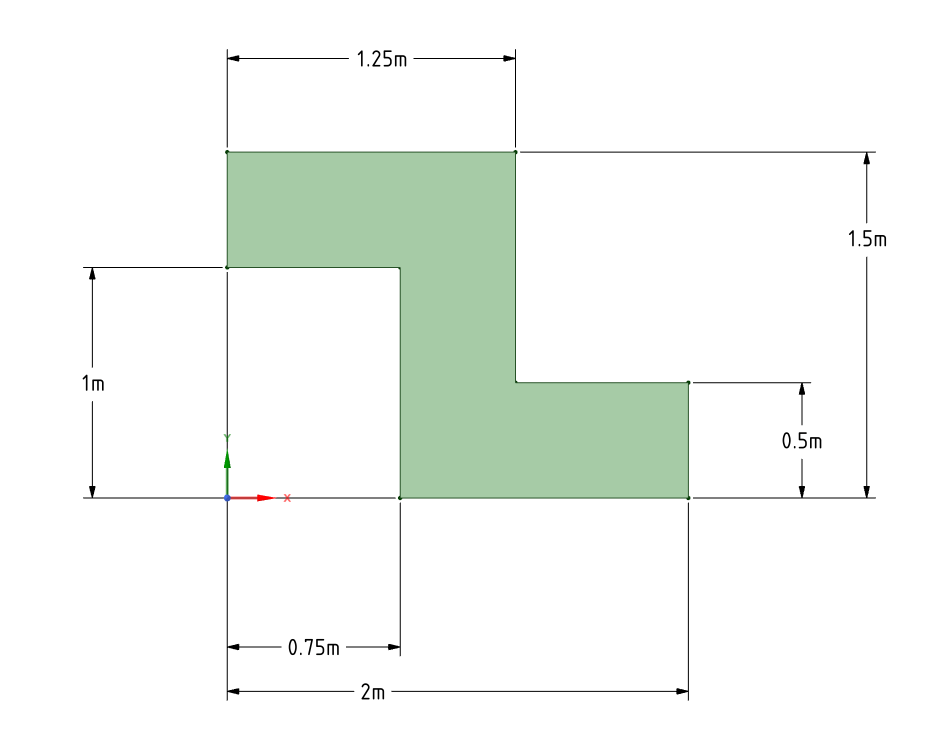
При тестировании я использовал следующую форму

и результаты center = [1.0, 0.75] а также mmoi = 787.5 соответствие с анализом, выполненным в пакете САПР

Вот модульный тест, который проверяет данные САПР:

[TestMethod, TestCategory("Linear Algebra, Planar")]
public void Geom_PlanarPolygonMass()
{
    Vector2[] points = new Vector2[] {
        Vector2.Cartesian(0.75, 0),
        Vector2.Cartesian(2, 0),
        Vector2.Cartesian(2, 0.5),
        Vector2.Cartesian(1.25, 0.5),
        Vector2.Cartesian(1.25, 1.5),
        Vector2.Cartesian(0, 1.5),
        Vector2.Cartesian(0, 1.0),
        Vector2.Cartesian(0.75, 1),
    };

    var rg = RigidBody2.FromShape(1500, points);

    Assert.AreEqual(1500, rg.Mass);
    CollectionAssert.AreEqual(Vector2.Cartesian(1.0, 0.75), rg.LocalCg, AbsComparer(TinyNumber));
    Assert.AreEqual(687.5, rg.LocalMmoi, DoubleEx.TinyNumber);
}

Answer 2

Уравнение для момента инерции довольно просто, и вы можете найти его объяснение здесь: https://en.wikipedia.org/wiki/Moment_of_inertia

Это использовалось, например, чтобы вывести уравнение, которое вы цитировали.

Как упоминал Энди Ньюман, выпуклый многоугольник можно рассматривать как состоящий из треугольников. Но суммирование их индивидуальных инерций не является решением - оно не даст правильного уравнения, которое учитывает ось вращения.

Таким образом, в основном вам нужно получить уравнение для вашего многоугольника относительно оси вращения, вокруг которой вы хотите его вращать.

Вам может пригодиться одна из следующих теорем, в зависимости от типа фигуры, которую вы имеете в виду:

• Теорема о перпендикулярной оси
• Правило растяжения
• Теорема о параллельной оси