Понимание вывода из statsmodels grangercausalitytests

Question

Я новичок в Granger Causality и буду признателен за любые советы по пониманию / интерпретации результатов вывода python statsmodels. Я построил два набора данных (функции синуса сдвинуты во времени с добавленным шумом)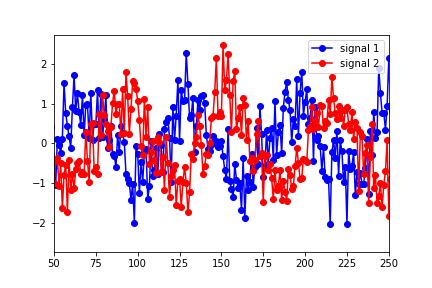

и поместите их в матрицу "данных" с сигналом 1 в качестве первого столбца и сигналом 2 в качестве второго. Затем я запустил тесты, используя:

granger_test_result = sm.tsa.stattools.grangercausalitytests(data, maxlag=40, verbose=True)`

Результаты показали, что оптимальное запаздывание (с точки зрения наибольшего значения F-теста) было для запаздывания 1.

Granger Causality
('number of lags (no zero)', 1)
ssr based F test:         F=96.6366 , p=0.0000  , df_denom=995, df_num=1
ssr based chi2 test:   chi2=96.9280 , p=0.0000  , df=1
likelihood ratio test: chi2=92.5052 , p=0.0000  , df=1
parameter F test:         F=96.6366 , p=0.0000  , df_denom=995, df_num=1

Однако запаздывание, которое, по-видимому, лучше всего описывает оптимальное перекрытие данных, составляет около 25 (на рисунке ниже сигнал 1 смещен вправо на 25 пунктов):

Granger Causality
('number of lags (no zero)', 25)
ssr based F test:         F=4.1891  , p=0.0000  , df_denom=923, df_num=25
ssr based chi2 test:   chi2=110.5149, p=0.0000  , df=25
likelihood ratio test: chi2=104.6823, p=0.0000  , df=25
parameter F test:         F=4.1891  , p=0.0000  , df_denom=923, df_num=25

Я явно неправильно что-то здесь понимаю. Почему прогнозируемое отставание не совпадает со сдвигом в данных?

Кроме того, может ли кто-нибудь объяснить мне, почему значения p настолько малы, что могут быть незначительными для большинства значений запаздывания? Они начинают появляться как ненулевые для лагов больше 30.

Спасибо за любую помощь, которую вы можете оказать.

Answer 1

Как указано здесь, для запуска теста причинности по Грейнджеру используемый вами временной ряд должен быть стационарным. Распространенный способ добиться этого - преобразовать обе серии, взяв первое различие каждого:

x = np.diff(x)[1:]
y = np.diff(y)[1:]

Вот сравнение результатов причинно-следственной связи Грейнджера при лаге 1 и лаге 25 для аналогичного набора данных, который я создал:

Без изменений

Granger Causality
number of lags (no zero) 1
ssr based F test:         F=19.8998 , p=0.0000  , df_denom=221, df_num=1
ssr based chi2 test:   chi2=20.1700 , p=0.0000  , df=1
likelihood ratio test: chi2=19.3129 , p=0.0000  , df=1
parameter F test:         F=19.8998 , p=0.0000  , df_denom=221, df_num=1

Granger Causality
number of lags (no zero) 25
ssr based F test:         F=6.9970  , p=0.0000  , df_denom=149, df_num=25
ssr based chi2 test:   chi2=234.7975, p=0.0000  , df=25
likelihood ratio test: chi2=155.3126, p=0.0000  , df=25
parameter F test:         F=6.9970  , p=0.0000  , df_denom=149, df_num=25

1-я разница

Granger Causality
number of lags (no zero) 1
ssr based F test:         F=0.1279  , p=0.7210  , df_denom=219, df_num=1
ssr based chi2 test:   chi2=0.1297  , p=0.7188  , df=1
likelihood ratio test: chi2=0.1296  , p=0.7188  , df=1
parameter F test:         F=0.1279  , p=0.7210  , df_denom=219, df_num=1

Granger Causality
number of lags (no zero) 25
ssr based F test:         F=6.2471  , p=0.0000  , df_denom=147, df_num=25
ssr based chi2 test:   chi2=210.3621, p=0.0000  , df=25
likelihood ratio test: chi2=143.3297, p=0.0000  , df=25
parameter F test:         F=6.2471  , p=0.0000  , df_denom=147, df_num=25

Попробую концептуально объяснить происходящее. Из-за того, что ряд, который вы используете, имеет четкую тенденцию к среднему, ранние запаздывания на 1, 2, ... и т. Д. Все дают важные прогностические модели в F-тесте. Это потому, что вы можете отрицательно коррелироватьx значения 1 отстают от yочень легко оценивается из-за долгосрочной тенденции. Вдобавок (это более обоснованное предположение), я думаю, что причина, по которой вы видите статистику F для лага 25 очень низкой по сравнению с ранними лагами, заключается в том, что большая часть дисперсии объясняетсяx ряд содержится в автокорреляции y от лагов 1-25, поскольку нестационарность дает автокорреляции большую предсказательную силу.

Answer 2

Из заметок https://www.statsmodels.org/dev/generated/statsmodels.tsa.stattools.grangercausalitytests.html

Нулевая гипотеза для тестов grangercausality состоит в том, что временной ряд во втором столбце, x2, НЕ Грейнджер вызывает временной ряд в первом столбце, x1. Причинность Grange означает, что прошлые значения x2 оказывают статистически значимое влияние на текущее значение x1, принимая во внимание прошлые значения x1 как регрессоры. Мы отвергаем нулевую гипотезу о том, что x2 не приводит к тому, что Грейнджер не вызывает x1, если значения ниже желаемого размера теста.

Нулевая гипотеза для всех четырех тестов состоит в том, что коэффициенты, соответствующие прошлым значениям второго временного ряда, равны нулю.

тест работает точно так, как ожидалось.

Давайте установим уровень значимости для вашего теста, скажем, альфа = 5% или 1%. Важно выбрать его перед выполнением теста. Затем вы запускаете тест Грейнджера (не) причинности, нулевая гипотеза которого состоит в том, что второй временной ряд не вызывает первого, в смысле Грейнджер, фиксированного запаздывания. Как вы обнаружили, значение для lag = 1 выше, чем пороговое значение альфа, которое вы установили, что означает, что вы можете отклонить нулевую гипотезу (то есть, нет причинно-следственной связи). Для лаг> 25 значения уменьшаются до нуля, что означает, что вы должны отказаться от нулевой гипотезы, то есть не причинности.

Это действительно согласуется с тем, что вы указали в качестве временных рядов по построению.

Answer 3

Кто-нибудь упомянул, что посылка в исходном вопросе была неверной?

«Результаты показали, что оптимальное отставание (с точки зрения наивысшего значения теста F) было для отставания 1. ..."

... это утверждение неверно. F-значения и chi2 получены из разных степеней свободы. Первая запаздывающая модель всегда имеет df=1. Это приводит к другому распределению результатов тестов, чем при df=25.

Вы не можете сравнивать оценки F-теста или хи2 для разных степеней свободы, поскольку они будут иметь разные распределения. Вместо этого вы сравниваете p-значения или, лучше, как отмечает @AstoundingJB, выбираете граничную альфу и игнорируете значение p-значения, смотрите только на двоичное решение о том, что оно меньше или больше альфы. Или выберите диапазон альфы, и если p-значение находится посередине, сделайте вывод, что тест неубедительный.

Кроме того, методология, предложенная @rsmith49, — это путь: удалить долгосрочные тенденции, взяв первое отличие. Но вы должны проверить (по крайней мере, на графике), что это делает временной ряд «стационарным». Если тенденция все еще сохраняется, сделайте еще одно различие или вручную вычтите из необработанных данных кривую, но если вы обнаружите, что вам нужно сделать это, полезность теста Грейнджера сомнительна, вы можете также попробовать тесты VAR: (https://en.wikipedia.org/wiki/Векторная_авторегрессия