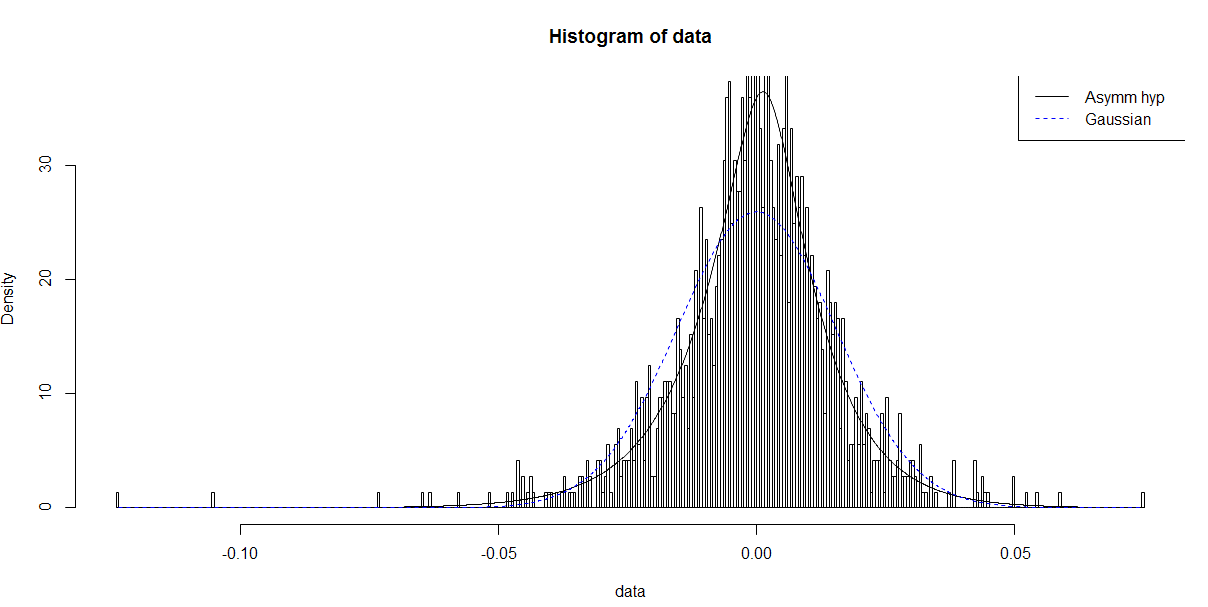
Как я могу определить вероятность события в R для гиперболического распределения?
Я хотел бы знать, как я могу рассчитать P ≥ -0.0001, Я новичок в математике, статистике и R.
В настоящее время я моделирую некоторые данные Spread в R. Я смог смоделировать данные для определенного распределения (в случае нижеприведенного примера это Гиперболический) и выполнить тест отношения правдоподобия, чтобы подтвердить жизнеспособность использования указанного распределения.
В моей голове, как только я получил распределение, я теперь, более надежно, могу вычислить мои вероятности, поскольку я более точно понимаю область под кривой?
Я предполагал, что смогу провести тест, подобный t-статистике, когда распределение будет сопоставлено, однако я не могу понять, как это сделать.
Я видел pnorm(x) функции, а также видел phyper Однако не могу понять, как просто рассчитать P ≥ -0.0001,
Ниже мой код, ваша помощь будет высоко ценится;
`# library (ghyp) библиотека (timeSeries)
# Coverting to Time Series
E <- timeSeries(A[,"Spread"])
# Fitting
ef <- (density(E))
ghdfit <- fit.ghypuv(E,symmetric = FALSE, control = list(maxit = 1000))
hypfit <- fit.hypuv(E,symmetric = FALSE, control = list(maxit = 1000))
nigfit <- fit.NIGuv(E,symmetric = FALSE, control = list(maxit = 1000))
# Density
ghddens <- dghyp(ef$x, ghdfit)
hypdens <- dghyp(ef$x, hypfit)
nigdens <- dghyp(ef$x, nigfit)
nordens <- dnorm(ef$x, mean = mean(E),sd = sd(c(E[,1])))
col.def <- c("black","red","green","orange")
plot(ef, xlab = " Spread ", ylab = expression(f(x)),ylim = c(0,50), main ='CABLE - 3 Day Comparison across 28 Years')
lines(ef$x, ghddens, col = "red")
lines(ef$x, hypdens, col = "blue")
lines(ef$x, nigdens, col = "green")
lines(ef$x, nordens, col = "orange")
legend("topleft", legend = c("Empirical","GHD","HYP","NIG","NORM"), col = col.def, lty = 1)
# QQ Plot
qqghyp(ghdfit, line = TRUE, ghyp.col = "red", plot.legend = FALSE, gaussian = FALSE, main = " ", cex = 0.8)
qqghyp(hypfit, add = TRUE, ghyp.pch = 2, ghyp.col = "green", gaussian = FALSE, line = FALSE, cex = 0.8)
qqghyp(nigfit,add = TRUE, ghyp.pch = 3, ghyp.col = "orange", gaussian = FALSE, line = FALSE, cex = 0.8)
legend("topleft", legend = c("GHD","HYP","NIG"), col = col.def[-c(1,5)], pch = 1:3)
# Diagnostic
options(scipen=999)
AIC <- stepAIC.ghyp(E, dist = c("ghyp","hyp","NIG"), symmetric = FALSE, control = list(maxit=1000))
LRghdnig <- lik.ratio.test(ghdfit,nigfit)
LRghdhyp <- lik.ratio.test(ghdfit,hypfit)
LRghdhyp $ статистика L 0.07005745
$ p.value 1 0.0211198
$ df 1 1
$ H0 1 ЛОЖЬ
Итак, я знаю правильное распределение и как его подогнать. Как мне определить вероятность > - 0.0001 происходит?