2D трассировка трассировки снаряда

Question

Задача трассировки снаряда в 2D игре:

Предположение:

Мы делаем упрощенное предположение, что гравитация постоянна и что нет ветра или сопротивления. Движение снаряда задается следующими уравнениями:

x = x0 + v0t cos (theta)

y = y0 + v0t sin (theta) +.5 gt ^ 2

где (x0, y0) - начальное положение, v0 - начальная скорость (только величина), тета - угол разряда и g - ускорение силы тяжести. Решив первое уравнение для v0t и подставив второе, получим уравнение [1]:

y = y0 + (x-x0) tan (тета) + .5 (г /v0^2) (x-x0)^2 / cos(тета) ^ 2

Калибровка:

Калибровка - это процесс определения значения g по фактическому снаряду. Для этого мы стреляем в случайный снаряд и захватываем:

1. Начальная точка (x0, y0)
2. Вектор прицела (v0, тета)
3. Случайная точка на кривой (x1, y1)

Подставляя значения в уравнение [1] и решая для g, получим:

g = (v0 ^ 2) * {[2 cos (тета)^2 (y1-y0) / (x1-x0)^2] - [sin(2theta) / (x1-x0)]}

Заявка:

Теперь, когда у нас есть g, мы можем подставить его обратно в уравнение [1], которое теперь можно использовать для отслеживания пути снаряда из любой начальной точки и начальной скорости. (это та часть, которую я не понимаю)

г =5,89

(x0, y0) начальная позиция = 0,0

Начальная скорость = 1-100

Угол разряда = 0-360

Может кто-нибудь объяснить, как получить полный путь траектории параболы для любой начальной скорости от 1 до 100 и для любого угла разряда от 0 до 360, если ускорение под действием силы тяжести составляет 5,89 (в этой игре), и начальный позиция 0,0?

Я - полный новичок в математике, все эти вещи не выделены жирным шрифтом, который я нашел в другом месте и ломал голову. Пожалуйста, предположите, что я ничего не знаю.

Answer 1

Выбор v0 = 10 а также theta = 60 degrees у нас есть

tan(theta) = 1.732
cos(theta) = 0.5

и, таким образом, уравнение 1 читает (x0=0, y0=0, g=5.89 были даны)

y = 1.732*x - 0.1178*x^2

который может быть нанесен непосредственно (y против x): смотрите здесь

Примечание: я исправил - знак гравитации.

Answer 2

Вы пропускаете только время t в своем первом наборе уравнений и пространственное / временное ограничение, строите первую x секунду снаряда или до тех пор, пока снаряд не покинет ограничивающую рамку m. так что псевдокод будет:

• т =0; х (0)= некоторая координата; y(0)= другая координата
• LOOP т
• т = Т +1
• Вычислить координаты {X(t=1), Y(t=1)}
• Нарисуйте точку или линию между этой точкой и предыдущей
• LOOP UNTIL t> ограничение по времени ИЛИ точка {X(t), Y(t)} находится за пределами вашей ограничительной рамки

Я надеюсь, что эта помощь в вашем деле

Answer 3

Это довольно простая проблема физики для студентов. Вы начинаете с закона Ньютона для x- и y-направлений:

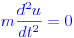
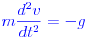
с начальными условиями:

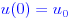
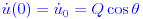
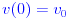
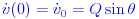
Где Q - начальная скорость снаряда, а тета - угол, измеренный против часовой стрелки от горизонта, если пистолет направлен вправо.

Поэтому, если вы интегрируете каждый из них по времени, вы получите:

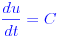
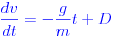
Применяя начальные условия:

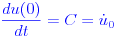
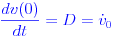
Интегрирование во второй раз дает:

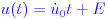
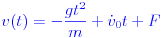
Применяя начальные условия снова:

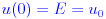
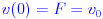
Выполнение замен дает окончательные уравнения, которые вы хотите для (u, v) позиции снаряда с момента, когда пистолет выстреливает:

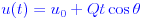
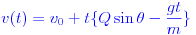
Если вы положите начало системы координат на выходе из дульного орудия, то два начальных смещения равны нулю.

Теперь у вас есть два уравнения для положения (u, v) снаряда. Вы можете подключить начальную скорость снаряда и угол наклона ружья, измеренные от горизонта в ноль, указывая вправо.

Вы просто начинаете с нулевого времени, выбираете приращение во времени и зацикливаетесь на столько времени, сколько хотите. Вы вставляете текущее значение времени в эти уравнения, оцениваете результаты, увеличиваете время и повторяете.

Давайте представим, что вы поворачиваете ружье под углом 45 градусов против часовой стрелки от горизонта и стреляете снарядом со скоростью 1000 дюймов в секунду. Вы можете шагать во времени и видеть, как снаряд движется вверх и вправо по параболической траектории, пока не достигнет своей вершины, а затем начнет падать обратно к горизонту. В конце концов ваше смещение по оси Y вернется к нулю, а затем продолжится в отрицательной области, как если бы вы стреляли с края обрыва.

Если вы хотите узнать, как далеко снаряд идет до того, как он упадет на землю, просто остановите цикл времени, когда высота станет меньше или равна нулю:

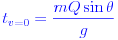
Вот реализация Java для вас:

package physics;

/**
 * CannonSimulator simulates shooting a projectile.  Users are responsible for making
 * sure that all constants use consistent units (e.g. meters for length, seconds for
 * time, kg for mass, etc.)
 * @author Michael
 * @since 6/14/12 9:47 PM
 * @link http://stackru.com/questions/10935060/2d-projectile-tracing-path-clarification/11043389#11043389
 */
public class CannonSimulator {

    private double m;
    private double g;
    private double q;
    private double theta;

    public static void main(String[] args) {
        double m = ((args.length > 0) ? Double.valueOf(args[0]) : 1.0); // default mass is 1 kg
        double g = ((args.length > 1) ? Double.valueOf(args[1]) : 9.8); // default gravity is 9.8 m/sec^2
        double q = ((args.length > 2) ? Double.valueOf(args[2]) : 100.0); // default velocity is 100 m/sec
        double theta = ((args.length > 3 ? Double.valueOf(args[3]) : Math.PI/4.0)); // default angle is 45 degrees
        CannonSimulator simulator = new CannonSimulator(m, g, q, theta);
        double t = 0.0;
        double dt = 0.001; // time increment of 0.1 seconds
        while (simulator.v(t) >= 0.0) {
            System.out.println(String.format("time: %10.3f u: %10.3f v: %10.3f", t, simulator.u(t), simulator.v(t)));
            t += dt;
        }
    }

    public CannonSimulator(double m, double g, double q, double theta) {
        if (m <= 0.0) throw new IllegalArgumentException("mass must be greater than zero");
        if (g <= 0.0) throw new IllegalArgumentException("gravity must be greater than zero");
        if (q <= 0.0) throw new IllegalArgumentException("velocity must be greater than zero");

        this.m = m;
        this.g = g;
        this.q = q;
        this.theta = theta;
    }

    public double v(double time) {
        return time*(q*Math.sin(theta) - g*time/m);
    }

    public double u(double time) {
        return time*q*Math.cos(theta);
    }
}

Вот как решить эту проблему.