Как вычислить внутренние контрольные точки для непрерывных бикубических пятен Безье на поверхности C2

Question

Я пытаюсь вычислить контрольные точки для бикубической поверхности Безье из плавно соединяющихся трубок. Этот пример дает 16 контрольных точек для соответствующего патча Безье (в синтаксисе OpenSCAD):

[[[ 2 ,  2 , 0], [2.5, 1.5, 0], [3.5,  1 , 0], [4,  1 , 0]],
 [[ 2 ,  2 , 1], [2.5, 1.5, 1], [3.5,  1 , 1], [4,  1 , 1]],
 [[1.3, 1.3, 2], [1.8,  0 , 2], [ 3 , 0.5, 2], [4, 0.5, 2]],
 [[ 0 ,  0 , 2], [1.8,  0 , 2], [ 3 ,  0 , 2], [4,  0 , 2]]]

Угловые точки даны; контрольные точки (показаны красным цветом) по краям были вычислены по касательным с очевидными направлениями: Пластырь можно отразить на плоскостях z=0, y=0, x=4 и x=y, чтобы создать большую составную поверхность, непрерывную по С1 по всем четырем швам. Эта поверхность также непрерывна по С2 по швам в плоскостях z = 0, y = 0 и x = 4, но не по шву в плоскости x=y (см. V-образные желтые нормальные векторы):

Для желаемой непрерывности C2 нормали поверхности вдоль нарушающего шва должны быть копланарными плоскости x=y.

Можно ли вообще установить четыре внутренних контрольных точки так, чтобы нормали по всем швам выходили по желанию?

Если да, то по какой формуле или алгоритму следует рассчитывать внутренние контрольные точки, чтобы обеспечить непрерывную составную поверхность C2?

Если нет, то каков подходящий подход для создания нужного патча?

Answer 1

Чтобы соединение между двумя кривыми Безье было непрерывным и гладким, три точки на стыке должны быть выровнены (как вы можете видеть желтым цветом на эскизе). Это потому, что на концах кривая всегда касается отрезка, образованного двумя последними точками.

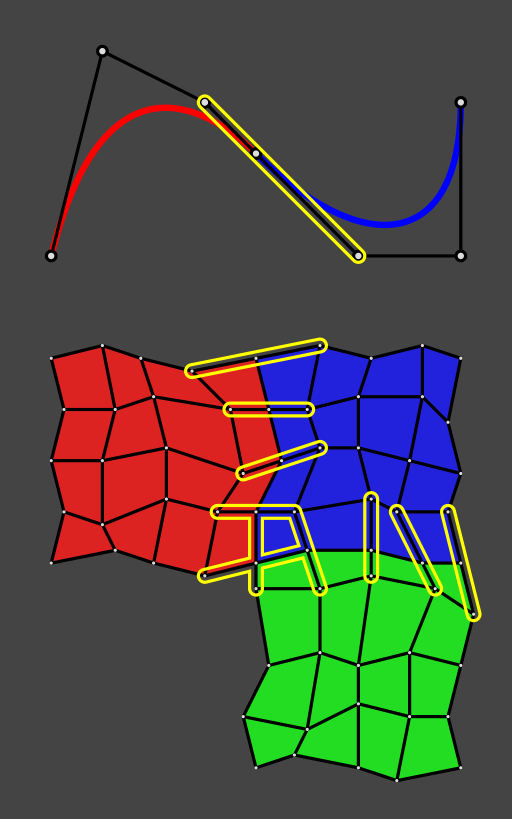
Тот же принцип можно применить к поверхностям Безье, которые вы видите внизу эскиза (также выделены желтым цветом). Я не думаю, что есть менее ограничительное решение.