[Octave] Использование fminunc не всегда дает согласованное решение

Question

Я пытаюсь найти коэффициенты в уравнении для моделирования шага двигателя, который имеет вид 1-e^x, Уравнение, которое я использую для моделирования, имеет вид

a(1)*t^2 + a(2)*t^3 + a(3)*t^3 + ...

(Получено в исследовательской работе, используемой для определения параметров двигателя)

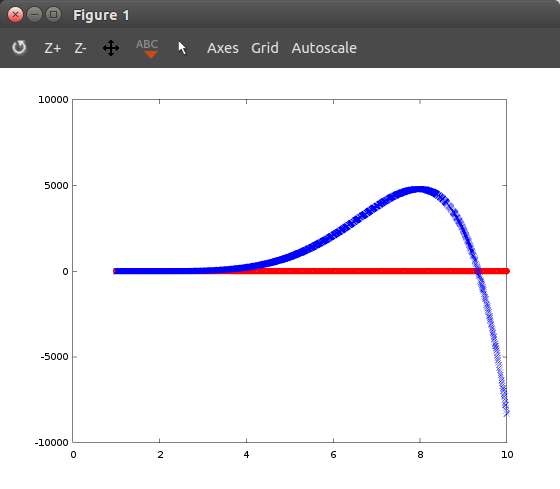
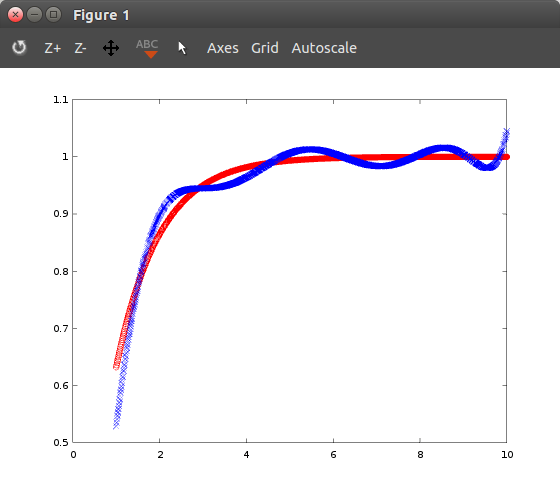
Иногда используя fminunc найти коэффициенты работает хорошо, и я получаю хороший результат, и он довольно хорошо соответствует обучающим данным. В других случаях возвращаемые коэффициенты ужасны (выходят за пределы, превышающие то, что должно быть на выходе, и на несколько порядков ниже). Это особенно происходит, когда я начал использовать термины более высокого порядка: используя любую модель, которая использует x^8 или выше (x^9, x^10, x^11и т. д.) всегда дает плохие результаты.

Поскольку иногда это работает, я не могу понять, почему моя реализация была бы неправильной. я пытался fminunc при обеспечении градиентов, а также при отсутствии градиентов, разницы нет. Я смотрел на использование других функций для решения коэффициентов, таких как polyfit, но в этом случае он должен иметь термины, которые взяты из 1 к члену высшего порядка, но модель, которую я использую, имеет наименьшую мощность в 2,

Вот основной код:

clear;

%Overall Constants
max_power = 7;

%Loads in data
%data = load('TestData.txt');
load testdata.mat

%Sets data into variables
indep_x = data(:,1); Y = data(:,2);

%number of data points
m = length(Y);

%X is a matrix with the independant variable
exps = [2:max_power];
X_prime = repmat(indep_x, 1, max_power-1); %Repeats columns of the indep var
X = bsxfun(@power, X_prime, exps);

%Initializes theta to rand vals
init_theta = rand(max_power-1,1);

%Sets up options for fminunc
options = optimset( 'MaxIter', 400, 'Algorithm', 'quasi-newton');

%fminunc minimizes the output of the cost function by changing the theta paramaeters
[theta, cost] = fminunc(@(t)(costFunction(t, X, Y)), init_theta, options)

%
Y_line = X * theta;

figure;
hold on; plot(indep_x, Y, 'or');
hold on; plot(indep_x, Y_line, 'bx');

И вот costFunction:

function [J, Grad] = costFunction (theta, X, Y)
   %# of training examples

   m = length(Y);

    %Initialize Cost and Grad-Vector
    J = 0;
    Grad = zeros(size(theta));

    %Poduces an output based off the current values of theta
    model_output = X * theta;

    %Computes the squared error for each example then adds them to get the total error
    squared_error = (model_output - Y).^2;
    J = (1/(2*m)) * sum(squared_error);

    %Computes the gradients for each theta t
    for t = 1:size(theta, 1)
        Grad(t) = (1/m) * sum((model_output-Y) .* X(:, t));
    end

endfunction

Любая помощь или совет будут оценены.

Answer 1

Попробуйте добавить регуляризацию к вашей функции стоимости:

function [J, Grad] = costFunction (theta, X, Y, lambda)
    m = length(Y);

    %Initialize Cost and Grad-Vector
    J = 0;
    Grad = zeros(size(theta));

    %Poduces an output based off the current values of theta
    model_output = X * theta;

    %Computes the squared error for each example then adds them to get the total error
    squared_error = (model_output - Y).^2;
    J = (1/(2*m)) * sum(squared_error);
    % Regularization
    J = J + lambda*sum(theta(2:end).^2)/(2*m);


    %Computes the gradients for each theta t
    regularizator = lambda*theta/m;
    % overwrite 1st element i.e the one corresponding to theta zero
    regularizator(1) = 0;
    for t = 1:size(theta, 1)
        Grad(t) = (1/m) * sum((model_output-Y) .* X(:, t)) + regularizator(t);
    end

endfunction

Срок регуляризации lambda используется для контроля скорости обучения. Начните с лямбда =1. Чем больше значение для лямбда, тем медленнее будет происходить обучение. Увеличьте лямбду, если описанное вами поведение сохраняется. Возможно, вам придется увеличить количество итераций, если лямбда становится высокой. Вы также можете рассмотреть вопрос о нормализации ваших данных, и некоторые эвристические методы инициализации тэты - установка всех тэта на 0,1 может быть лучше случайной. Если ничего другого, это обеспечит лучшую воспроизводимость от обучения к обучению.