Быстрая, грубая версия atan2() для C/Objective-C/Swift?
Я работаю над графическим кодом, который в реальном времени рисует плавные, непрерывные кривые. Я хочу добавить поддержку пернатых кистей. Для этого мне нужно уметь вычислять "нормали" или линии, перпендикулярные отрезкам, которые составляют мою кривую.
Чистый математический способ сделать это - использовать арктан, чтобы найти угол сегмента, повернуть на 90 градусов и использовать синус и косинус, чтобы найти смещения x и y моих нормалей. После того, как у меня появятся мои углы, было бы довольно легко использовать справочную таблицу для замены синуса и косинуса, но написать эффективную, низкую точность версии atan2() кажется хитрым.
Длина и углы моих нормалей (перпендикулярных линий) не должны быть точными. Если это на одну десятую, это не имеет значения.
Кто-нибудь из вас разработал высокоскоростную, сырую версию atan2() для такого рода графической работы? Оптимизация такого рода вещей для производительности сложна и занимает много времени.
Я работаю в Swift 3, но я "многоязычный". Я в порядке с интеграцией кода, написанного на C/Objective-C, а также. (или, возможно, преобразовать его в Swift.)
РЕДАКТИРОВАТЬ:
Больше деталей:
Проект включает в себя рисование от руки, которое предоставляет ряд точек, которые иногда довольно далеко друг от друга, если пользователь быстро проводит пальцем, и использование сплайнов Catmull-Rom для добавления промежуточных точек для создания серии отрезков линий, достаточно маленьких, чтобы они выглядели как гладкая кривая.
(Сплайны Кэтмулла-Рома - это кривая, похожая на более известную кривую Безье, но все контрольные точки кривой лежат на кривой, поэтому сгладить кривую просто, пользователь вводит "от руки", используя входные вершины для сделать сглаживание.)
(Отныне я буду ссылаться на "кривые", но на самом деле я имею в виду полилинии, состоящие из отрезков, настолько коротких, что они кажутся гладкими кривыми)
Я разложил свой код так, чтобы генерировать сплайны только для тех частей кривой, которые изменились. Теперь это довольно быстро и создает красивые плавные кривые так быстро, как вы можете рисовать. Субъективно, кажется, что я рисую кривую, которая следит за вашим пальцем, отслеживая точку за точкой, без прыжков между точками.
Следующая цель - рисовать кистью с мягкими краями. Для этого я хочу найти кривые слева и справа от отпечатка пальца пользователя, которые параллельны кривой. Затем я буду использовать OpenGL для создания треугольных полос, которые определяют толстую кривую между левой и правой линиями, и использовать многоугольную штриховку, чтобы растушевать кривую от непрозрачной вдоль кривой отпечатка пальца пользователя до прозрачной вдоль левой и правой параллельных кривых.
Скажем, я хочу нарисовать кривую с мягкими краями толщиной 6 пунктов. Кривые, которые следуют за отпечатком пальца пользователя слева и справа, должны были бы расширяться на 3 точки от кривой пользователя.
Я планирую найти вершины конечных точек для левой и правой кривых, найдя отрезки линии, перпендикулярные отрезкам линии дорожки пальца пользователя, которые проходят через вершины дорожки пальца и расширяются на 1/2 желаемой толщины линии слева и справа от отпечатка пальца пользователя.
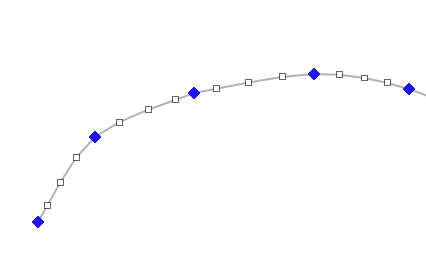
Ниже приведен снимок экрана с кривой, нарисованной текущей версией программы, с входными вершинами, нарисованными в виде синих ромбов, а точки сглаживания, которые я добавил, нарисованы в виде полых квадратов. (Я уменьшил количество добавленных точек сглаживания, чтобы вы могли лучше видеть, что происходит.)
Представьте себе, что вы проводите серию "хеш-меток" через каждую из точек вершины, каждая из которых имеет длину 6 точек, с центром в одной из этих точек вершины и перпендикулярно первому отрезку прямой линии сглаженной кривой, которая заканчивается в этой вершине.
Как отметил в своем ответе Питер О., найти отрезок, перпендикулярный любому отрезку, очень просто - вы просто инвертируете наклон. Однако я хочу отрезки определенной длины. (В моем примере 6 точек, 3 точки по обе стороны от вершины.) Я ищу способ сделать это быстро. Я мог вычислить конечные точки моих нормалей, используя триг или квадратные корни, которые очень медленные.
1 ответ
Для вашей проблемы, если все, что вам нужно, это найти линию, которая перпендикулярна другой, вам даже не нужно использовать atan2; Вместо этого вы можете использовать следующий подход. Пусть (x1, y1) и (x2, y2) будут входным отрезком.
// Find deltas
dx=x2-x1
dy=y2-y1
// Find perpendicular vector to (dx, dy)
pdx=-dy
pdy=dx
// Normalize the vector to a unit vector
length=sqrt(pdx*pdx+pdy*pdy)
if(length!=0){
invlength=1.0/length
// Scale the vector as desired
invlength*=scale
pdx*=invlength
pdy*=invlength
}
// Now, find a line segment parallel to the vector
x2=x1+pdx
y2=y1+pdy
В качестве альтернативы, если вы настаиваете на atan2Я знаю об одной реализации общественного достояния на http://www.dspguru.com/dsp/tricks/fixed-point-atan2-with-self-normalization. Попробуйте оба подхода и посмотрите, какой лучше подходит для вашей цели.
В общем, если вы звоните atan2(dy,dx) просто чтобы получить правильный угол для cos а также sinчасто можно просто использовать компоненты x и y нормализованного (dx, dy) вектор, чтобы получить косинус и синус вместо, соответственно.