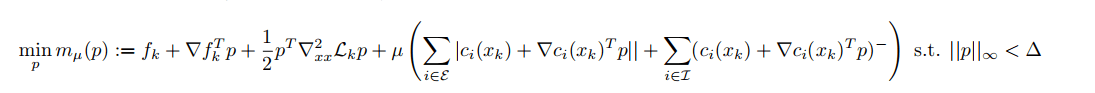Как минимизировать квадратичную целевую функцию с помощью основанного на доверительной области l1 штрафного последовательного квадратичного программирования

Question

Я хочу минимизировать неопределенную квадратичную функцию с ограничениями как равенства, так и неравенства. Итак, я пытаюсь реализовать последовательное квадратичное программирование с политикой штрафов l1, основанной на методе области доверия.

Я использую интерфейс cvxpy для того же.

Например, у меня есть следующий код,

import numpy as np
import cvxpy


# from : https://stackru.com/questions/31206443/numpy-second-derivative-of-a-ndimensional-array
def hessian_and_grad(x):
    """
    Calculate the hessian matrix with finite differences
    Parameters:
       - x : ndarray
    Returns:
       an array of shape (x.dim, x.ndim) + x.shape
       where the array[i, j, ...] corresponds to the second derivative x_ij
    """
    x_grad = np.gradient(x)
    hessian = np.empty((x.ndim, x.ndim) + x.shape, dtype=x.dtype)
    for k, grad_k in enumerate(x_grad):
        # iterate over dimensions
        # apply gradient again to every component of the first derivative.
        tmp_grad = np.gradient(grad_k)
        for l, grad_kl in enumerate(tmp_grad):
            hessian[k, l, :, :] = grad_kl
    return np.array(x_grad), hessian

def dispShape(P,grad_P, hess_P, cons1, grad_cons1, hess_cons1, cons2, grad_cons2, hess_cons2):
    print "P"
    print P.shape
    print "grad_P"

    print grad_P.shape
    print "hess_P"

    print hess_P.shape
    print "cons1"

    print cons1.shape
    print "grad_cons1"

    print grad_cons1.shape
    print "hess_cons1"

    print hess_cons1.shape
    print "grad_cons2"

    print grad_cons2.shape
    print "hess_cons2"

    print hess_cons2.shape


def disp(P,grad_P, hess_P, cons1, grad_cons1, hess_cons1, cons2, grad_cons2, hess_cons2):
    print "P"
    print P
    print "grad_P"

    print grad_P
    print "hess_P"

    print hess_P
    print "cons1"

    print cons1
    print "grad_cons1"

    print grad_cons1
    print "hess_cons1"

    print hess_cons1
    print "grad_cons2"

    print grad_cons2
    print "hess_cons2"

    print hess_cons2



P = np.array([[ 2., -4.,  0.],
             [ 0.,  4., -4.],
             [ 0.,  0.,  2.]])

q = np.array([ 0.,  0.,  0.])

A = np.array([[-1.,  1.,  0.],
             [ 0., -1.,  1.],
             [ 1.,  0.,  0.],
             [ 0.,  0.,  1.],
             [ 1.,  0.,  0.],
             [ 0.,  0.,  1.],
             [ 1.,  0.,  0.],
             [ 0.,  1.,  0.],
             [ 0.,  0.,  1.]])

lbA =   np.array([-0.3,-0.3, 0.2,0.7,0.2,0.7,-0.3,-0.3,-0.3])
ubA =   np.array([ 0.3, 0.3,0.2,0.7,0.2,0.7,1.1,1.1,1.1])
P = .5 * (P + P.T) + 1e-08 * np.eye(P.shape[0])



mu = 1  # Penalty parameter


# Define CVXPY problem
x = cvxpy.Variable(P.shape[1])
x_0 =   np.array([ 0.2, 0.5, 0.7])
# p = cvxpy.Variable(P.shape[1])

grad_P, hess_P = hessian_and_grad(P)
cons1 = np.subtract(np.matmul(A, x_0), ubA)
cons2 = np.add(np.matmul(-A, x_0), lbA)
grad_cons1, hess_cons1 = hessian_and_grad(cons1)
grad_cons2, hess_cons2 = hessian_and_grad(cons2)
dispShape(P,grad_P, hess_P, cons1, grad_cons1, hess_cons1, cons2, grad_cons2, hess_cons2)

hess_cons1 =hess_cons1.reshape((hess_cons1.shape[2],))
hess_cons2 =hess_cons1.reshape((hess_cons2.shape[2],))
hess_P =  hess_P.reshape((hess_P.shape[0] * hess_P.shape[1]) * hess_P.shape[2], hess_P.shape[3] )
grad_P =  grad_P.reshape((grad_P.shape[0] * grad_P.shape[1]), grad_P.shape[2] )

dispShape(P,grad_P, hess_P, cons1, grad_cons1, hess_cons1, cons2, grad_cons2, hess_cons2)

objective = cvxpy.quad_form(x, P) + q * x
p = cvxpy.Variable(hess_P.shape[0])


objective_model = cvxpy.quad_form(p, hess_P) + grad_P * p
objective_model += objective + mu * (cvxpy.norm1(cons1 + grad_cons1 * p) + cvxpy.norm1(cons2 + grad_cons2 * p))


# # Penalty part of the objective
# # objective += mu * (cvxpy.norm1(A * x - ubA) + cvxpy.norm1(-A * x + lbA))
# # objective_model = objective + mu * (cvxpy.norm1((A * x + np.gradient(A)) - ubA ) + cvxpy.norm1((-A * x - np.gradient(A)) + lbA ))
problem = cvxpy.Problem(cvxpy.Minimize(objective_model))
objective_osqp_cvxpy = problem.solve(solver=cvxpy.SCS, verbose=True)
print "Results: ", np.round(x.value, 3)

Я использовал,

 hess_cons1 =hess_cons1.reshape((hess_cons1.shape[2],))
    hess_cons2 =hess_cons1.reshape((hess_cons2.shape[2],))
    hess_P =  hess_P.reshape((hess_P.shape[0] * hess_P.shape[1]) * hess_P.shape[2], hess_P.shape[3] )
    grad_P =  grad_P.reshape((grad_P.shape[0] * grad_P.shape[1]), grad_P.shape[2] )

преобразовать 2d и 3d массивы в 1d массив. это нормально?

Когда я пытаюсь выполнить это, я получаю следующую ошибку

  Traceback (most recent call last):
  File "/home/mahesh/temp1.py", line 124, in <module>
    objective_model = cvxpy.quad_form(p, hess_P) + grad_P * p
  File "/usr/local/lib/python2.7/dist-packages/cvxpy-1.0.0-py2.7-linux-x86_64.egg/cvxpy/atoms/quad_form.py", line 209, in quad_form
    raise Exception("Invalid dimensions for arguments.")
Exception: Invalid dimensions for arguments.

Может ли кто-нибудь помочь мне, как сформулировать эту проблему и решить ее? Кроме того, мне нужно знать, как я могу получить значение нарушения ограничений, чтобы я мог выполнять итерацию дальше, чтобы найти оптимальное значение.

заранее спасибо