Куб с использованием одного GL_TRIANGLE_STRIP
Можно ли нарисовать целый куб, используя только один GL_TRIANGLE_STRIP?
Очевидно, что здесь меня интересует только комбинаторика куба, его можно было бы растянуть в любую коробку или подобный объект.
6 ответов
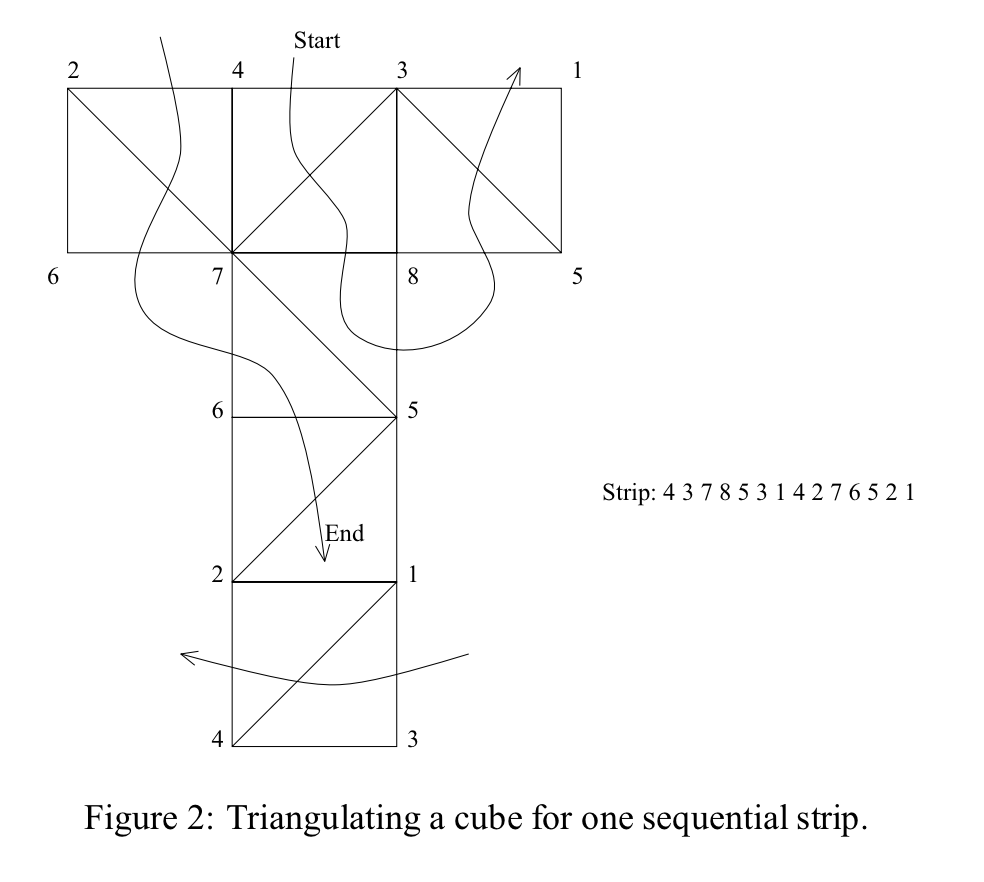
Из статьи " Оптимизация треугольных полос для быстрой визуализации " Эванса, Шиены и Варшни:
Для тех из вас, кто ленив (как и я), вот версия для копирования Роба Мейоффа "вставь-вставь";)
static const GLfloat cube_strip[] = {
-1.f, 1.f, 1.f, // Front-top-left
1.f, 1.f, 1.f, // Front-top-right
-1.f, -1.f, 1.f, // Front-bottom-left
1.f, -1.f, 1.f, // Front-bottom-right
1.f, -1.f, -1.f, // Back-bottom-right
1.f, 1.f, 1.f, // Front-top-right
1.f, 1.f, -1.f, // Back-top-right
-1.f, 1.f, 1.f, // Front-top-left
-1.f, 1.f, -1.f, // Back-top-left
-1.f, -1.f, 1.f, // Front-bottom-left
-1.f, -1.f, -1.f, // Back-bottom-left
1.f, -1.f, -1.f, // Back-bottom-right
-1.f, 1.f, -1.f, // Back-top-left
1.f, 1.f, -1.f // Back-top-right
};
Да, после небольшого количества экспериментов я нашел ответ сам. Представьте, что углы вашего куба окрашены попеременно в черный и белый цвета. Нарисуйте треугольный край вдоль каждой грани между двумя черными углами. Таким образом, диагонали образуют тетраэдр внутри куба. Для куба [0,1]³ возможная последовательность координат будет следующей:
Vertex Triangle Face
------+-----------+-----
0 0 0
0 1 0
1 0 0 000 010 100 **0
1 1 0 100 010 110 **0
1 1 1 100 110 111 1**
0 1 0 111 110 010 *1*
0 1 1 111 010 011 *1*
0 0 1 011 010 001 0**
1 1 1 011 001 111 **1
1 0 1 111 001 101 **1
1 0 0 111 101 100 1**
0 0 1 100 101 001 *0*
0 0 0 100 001 000 *0*
0 1 0 000 001 010 0**
Упомянутая выше бумага имеет треугольники, накрученные в неправильном направлении, однако есть простое исправление, обратный порядок вершин, и он станет лицевой стороной наружу (а не внутрь).
1 2 5 6 7 2 4 1 3 5 8 7 3 4
А вот набор вершин для единичного куба. Вы можете применить к этому преобразование и визуализировать ограничивающие рамки (выровненные по осям или ориентированные).
static const std::array<float> cube_strip = {
+0.5, +0.5, -0.5, // Back-top-right
-0.5, +0.5, -0.5, // Back-top-left
+0.5, -0.5, -0.5, // Back-bottom-right
-0.5, -0.5, -0.5, // Back-bottom-left
-0.5, -0.5, +0.5, // Front-bottom-left
-0.5, +0.5, -0.5, // Back-top-left
-0.5, +0.5, +0.5, // Front-top-left
+0.5, +0.5, -0.5, // Back-top-right
+0.5, +0.5, +0.5, // Front-top-right
+0.5, -0.5, -0.5, // Back-bottom-right
+0.5, -0.5, +0.5, // Front-bottom-right
-0.5, -0.5, +0.5, // Front-bottom-left
+0.5, +0.5, +0.5, // Front-top-right
-0.5, +0.5, +0.5, // Front-top-left
};
May be useful to some, here's a geometry shader that will take in a point and output a triangle strip of a unit cube
#version 410
layout(points) in;
layout(triangle_strip, max_vertices = 12) out;
uniform mat4 mvp;
void main() {
vec4 center = gl_in[0].gl_Position;
vec4 dx = mvp[0];
vec4 dy = mvp[1];
vec4 dz = mvp[2];
vec4 p1 = center;
vec4 p2 = center + dx;
vec4 p3 = center + dy;
vec4 p4 = p2 + dy;
vec4 p5 = p1 + dz;
vec4 p6 = p2 + dz;
vec4 p7 = p3 + dz;
vec4 p8 = p4 + dz;
gl_Position = p7;
EmitVertex();
gl_Position = p8;
EmitVertex();
gl_Position = p5;
EmitVertex();
gl_Position = p6;
EmitVertex();
gl_Position = p2;
EmitVertex();
gl_Position = p8;
EmitVertex();
gl_Position = p4;
EmitVertex();
gl_Position = p7;
EmitVertex();
gl_Position = p3;
EmitVertex();
gl_Position = p5;
EmitVertex();
gl_Position = p1;
EmitVertex();
gl_Position = p2;
EmitVertex();
gl_Position = p3;
EmitVertex();
gl_Position = p4;
EmitVertex();
}
В этой версии также есть координаты текстуры на случай, если они вам понадобятся.
Я проверил это с помощью WebGL, и куб имеет правильное отображение текстуры, но имеет особенности из-за того, что вам действительно нужны три координаты текстуры для каждого угла - по одной для каждой грани. Из-за этого вы можете использовать эти UV-развертки с бесшовной текстурой, но вы не можете «раскрасить» шесть сторон куба.
const verticies = [
-1, -1, -1, // 4
+1, -1, -1, // 3
-1, -1, +1, // 7
+1, -1, +1, // 8
+1, +1, +1, // 5
+1, -1, -1, // 3
+1, +1, -1, // 1
-1, -1, -1, // 4
-1, +1, -1, // 2
-1, -1, +1, // 7
-1, +1, +1, // 6
+1, +1, +1, // 5
-1, +1, -1, // 2
+1, +1, -1, // 1
];
const u0 = 0;
const u1 = 1;
const v0 = 0;
const v1 = 1 / 3;
const v2 = 2 / 3;
const v3 = 1;
const uvs = [
u0, v1, // 4
u0, v2, // 3
u1, v1, // 7
u1, v2, // 8
u1, v3, // 5
u0, v2, // 3
u0, v3, // 1
u0, v1, // 4
u0, v0, // 2
u1, v1, // 7
u1, v0, // 6
u1, v2, // 5
u0, v0, // 2
u0, v3, // 1
];