Подгонка логнормального распределения к уже скомпонованному питону данных

Question

Я хотел бы сделать логарифмическую подгонку к моим уже сохраненным данным. Сюжет бара выглядит так: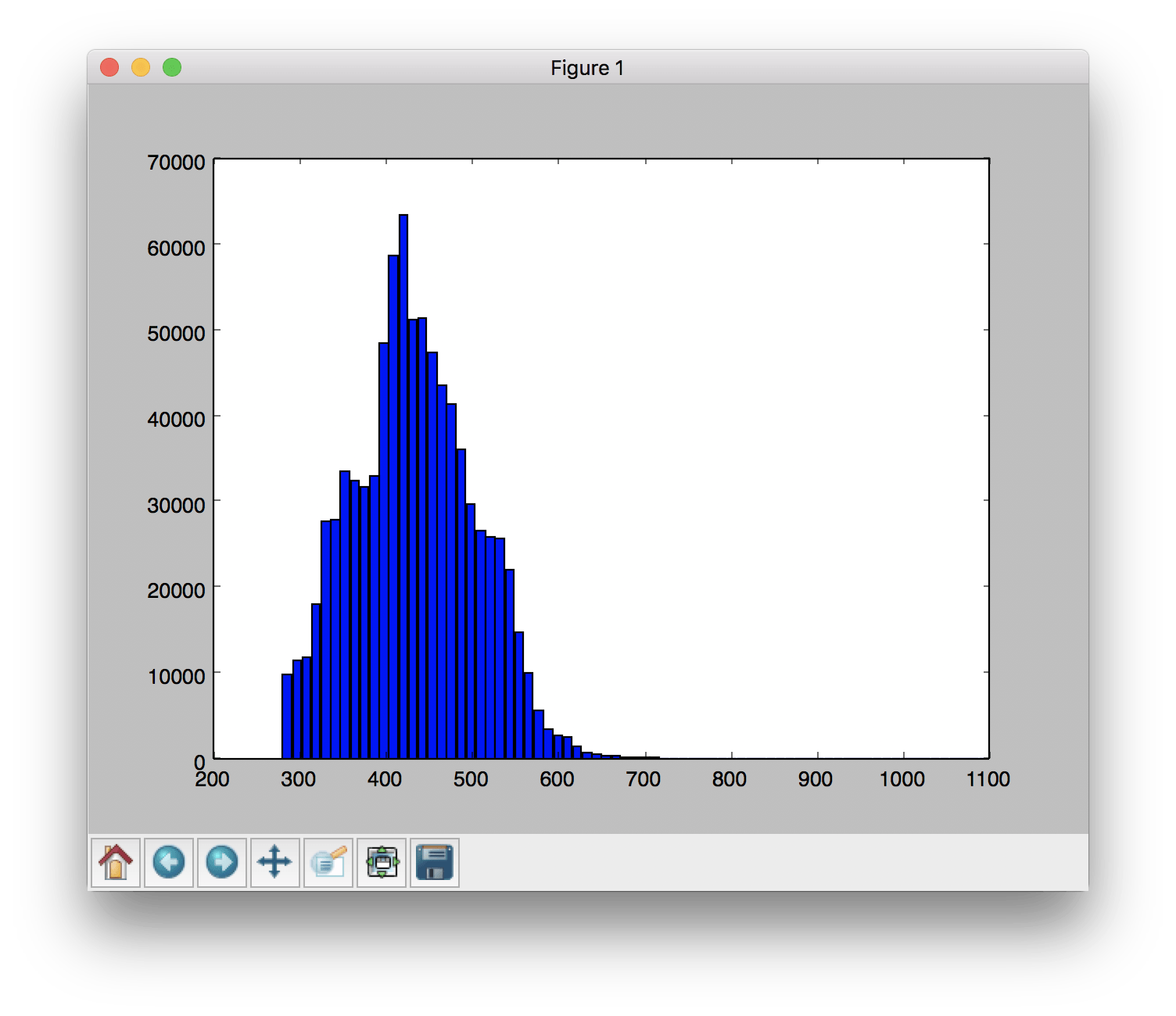

К сожалению, когда я пытаюсь использовать стандарт lognorm.pdf() форма подогнанного распределения очень различна. Я думаю, это потому, что мои данные уже отправлены в корзину. Вот код:

times, data, bin_points = ReadHistogramFile(filename)

xmin = 200
xmax = 800
x = np.linspace(xmin, xmax, 1000)
shape, loc, scale = stats.lognorm.fit(data, floc=0)
pdf = stats.lognorm.pdf(x, shape, loc=loc, scale=scale)

area=data.sum()
plt.bar(bars, data, width=10, color='b')
plt.plot(x*area, pdf, 'k' )

Вот как выглядит подобранный дистрибутив: 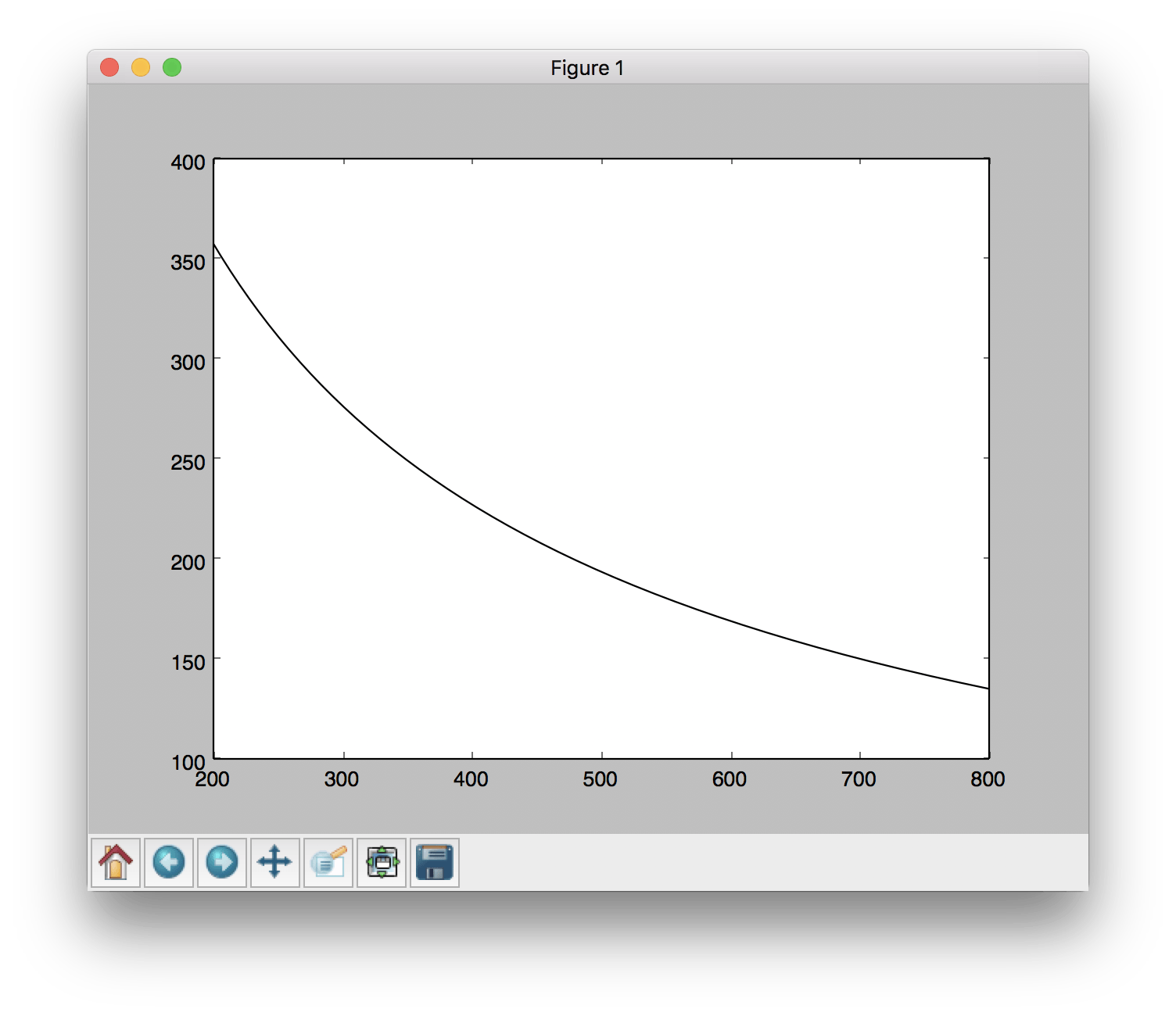Очевидно, что что-то не так с масштабированием. Я меньше беспокоюсь об этом, хотя. Моя главная проблема заключается в форме распределения. Это может быть дубликатом этого вопроса, но я не смог найти правильного решения. Я попробовал это и все еще получил очень похожую форму, как при выполнении вышеупомянутого. Спасибо за любую помощь!

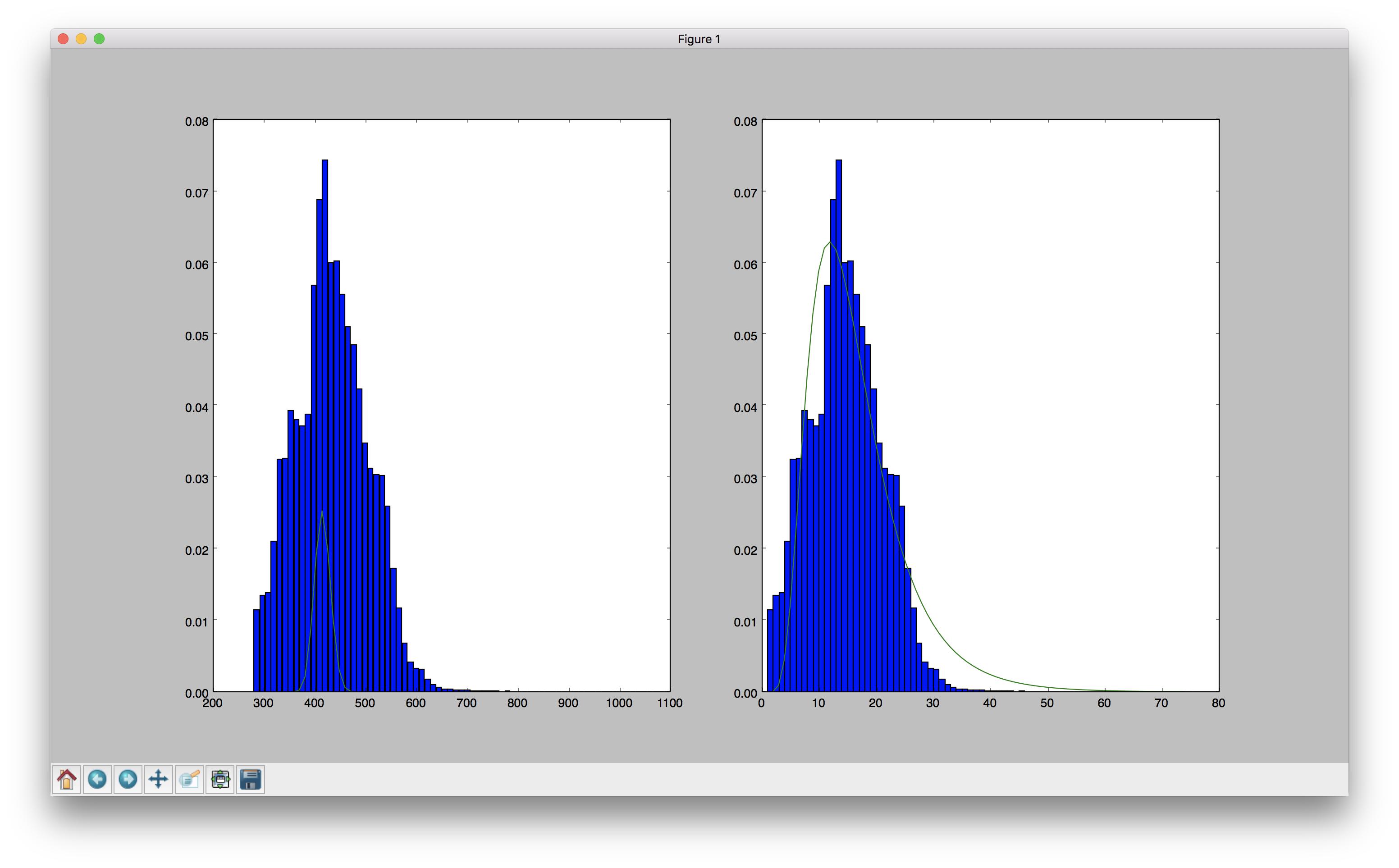
Обновление: с помощью curve_fit() Я был в состоянии привести себя в форму. Но я еще не доволен. Я хотел бы иметь оригинальные мусорные ведра и не единственные мусорные ведра. Также я не уверен, что именно происходит, и если это не подходит лучше. Вот код:

def normalize_integral(data, bin_size):
normalized_data = np.zeros(size(data))
print bin_size
sum = data.sum()
integral = bin_size*sum
for i in range(0, size(data)-1):
    normalized_data[i] = data[i]/integral

print 'integral:', normalized_data.sum()*bin_size
return normalized_data



def pdf(x, mu, sigma):
"""pdf of lognormal distribution"""

return (np.exp(-(np.log(x) - mu)**2 / (2 * sigma**2)) / (x * sigma * np.sqrt(2 * np.pi)))


bin_points=np.linspace(280.5, 1099.55994, len(bin_points))
data=[9.78200000e+03 1.15120000e+04 1.18000000e+04 1.79620000e+04 2.76980000e+04   2.78260000e+04   3.35460000e+04   3.24260000e+04 3.16500000e+04   3.30820000e+04   4.84560000e+04   5.86500000e+04 6.34220000e+04   5.11880000e+04   5.13180000e+04   4.74320000e+04 4.35420000e+04   4.13400000e+04   3.60880000e+04   2.96900000e+04 2.66640000e+04   2.58720000e+04   2.57560000e+04   2.20960000e+04 1.46880000e+04   9.97200000e+03   5.74200000e+03   3.52000000e+03 2.74600000e+03   2.61800000e+03   1.50000000e+03   7.96000000e+02 5.40000000e+02   2.98000000e+02   2.90000000e+02   2.22000000e+02 2.26000000e+02   1.88000000e+02   1.20000000e+02   5.00000000e+01 5.40000000e+01   5.80000000e+01   5.20000000e+01   2.00000000e+01 2.80000000e+01   6.00000000e+00   0.00000000e+00   0.00000000e+00 0.00000000e+00   0.00000000e+00   0.00000000e+00   0.00000000e+00 0.00000000e+00   0.00000000e+00   0.00000000e+00   0.00000000e+00 0.00000000e+00   0.00000000e+00   0.00000000e+00   0.00000000e+00 0.00000000e+00   0.00000000e+00   0.00000000e+00   0.00000000e+00 0.00000000e+00   0.00000000e+00   0.00000000e+00   0.00000000e+00 0.00000000e+00   0.00000000e+00   0.00000000e+00   0.00000000e+00 0.00000000e+00   0.00000000e+00]
normalized_data_unitybins = normalize_integral(data,1)


plt.figure(figsize=(9,4))
ax1=plt.subplot(121)
ax2=plt.subplot(122)
ax2.bar(unity_bins, normalized_data_unitybins, width=1, color='b')
fitParams, fitCov = curve_fit(pdf, unity_bins, normalized_data_unitybins, p0=[1,1],maxfev = 1000000)
fitData=pdf(unity_bins, *fitParams)
ax2.plot(unity_bins, fitData,'g-')

ax1.bar(bin_points, normalized_data_unitybins, width=10, color='b')
fitParams, fitCov = curve_fit(pdf, bin_points, normalized_data_unitybins, p0=[1,1],maxfev = 1000000)
fitData=pdf(bin_points, *fitParams)
ax1.plot(bin_points, fitData,'g-')

Answer 1

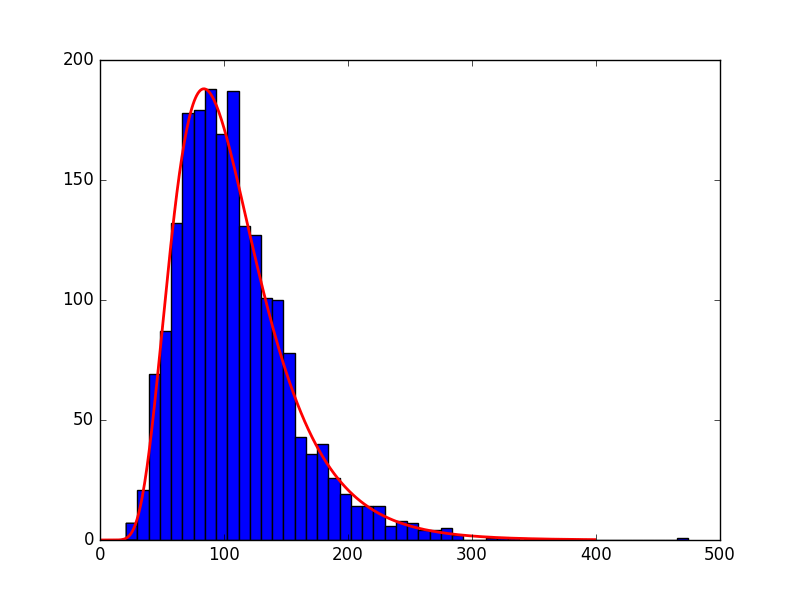
Как вы упоминаете, вы не можете использовать lognorm.fitна двоичных данных. Поэтому все, что вам нужно сделать, это восстановить необработанные данные из гистограммы. Очевидно, что это не "без потерь", чем больше бинов, тем лучше.

Пример кода с некоторыми сгенерированными данными:

import numpy as np
import scipy.stats as stats
import matplotlib.pylab as plt


# generate some data
ln = stats.lognorm(0.4,scale=100)
data = ln.rvs(size=2000)

counts, bins, _ = plt.hist(data, bins=50)
# note that the len of bins is 51, since it contains upper and lower limit of every bin

# restore data from histogram: counts multiplied bin centers
restored = [[d]*int(counts[n]) for n,d in enumerate((bins[1:]+bins[:-1])/2)]
# flatten the result
restored = [item for sublist in restored for item in sublist]

print stats.lognorm.fit(restored, floc=0)

dist = stats.lognorm(*stats.lognorm.fit(restored, floc=0))
x = np.arange(1,400)
y = dist.pdf(x)

# the pdf is normalized, so we need to scale it to match the histogram
y = y/y.max()
y = y*counts.max()

plt.plot(x,y,'r',linewidth=2)
plt.show()