Нейронные сети (или аналогичные) для проблем регрессии
Мотивирующая идея, лежащая в основе нейронных сетей, заключается в том, что они изучают "правильные" функции, к которым применяется логистическая регрессия. Есть ли подобный подход для линейной регрессии? (или просто проблемы регрессии в целом?)
Имеет ли смысл сделать очевидную работу по удалению применения сигмовидной функции для всех нейронов (т.е. включая скрытые слои)? (т.е. каждый нейрон выполняет линейную регрессию вместо логистической регрессии).
В качестве альтернативы, будет ли работать (возможно, даже более очевидно) просто масштабирование выходных значений до [0,1]? (Интуитивно я думаю, что нет, так как сигмоидная функция, кажется, заставит сеть произвольно отдавать предпочтение экстремальным значениям) (правка: хотя я просто искал еще немного и увидел, что один из методов - масштабирование на основе среднего и дисперсии, кажется, что это может иметь дело с этой проблемой - так что, возможно, это более жизнеспособно, чем я думал).
Или есть какой-то другой метод для "изучения особенностей" для проблем регрессии?
1 ответ
Проверьте этот апплет. Попробуйте выучить разные функции. Когда вы диктуете функции линейной активации как на скрытом, так и на выходном слоях, она даже не может узнать квадратичную функцию. Как минимум один слой должен быть настроен на сигмовидную функцию, см. Рисунки ниже.
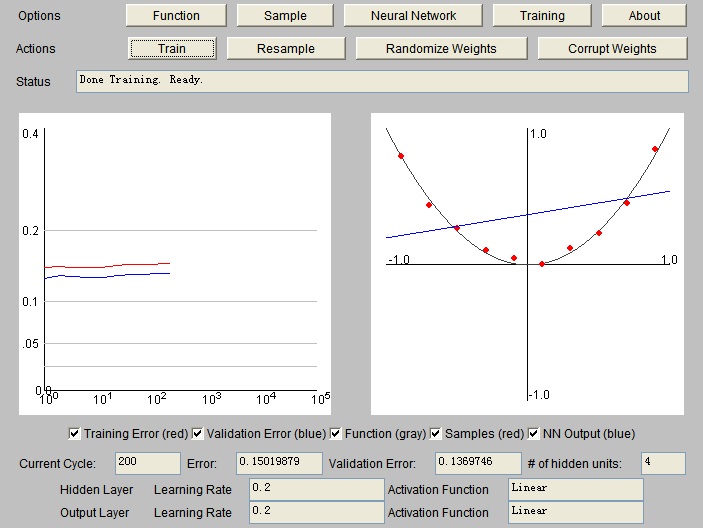
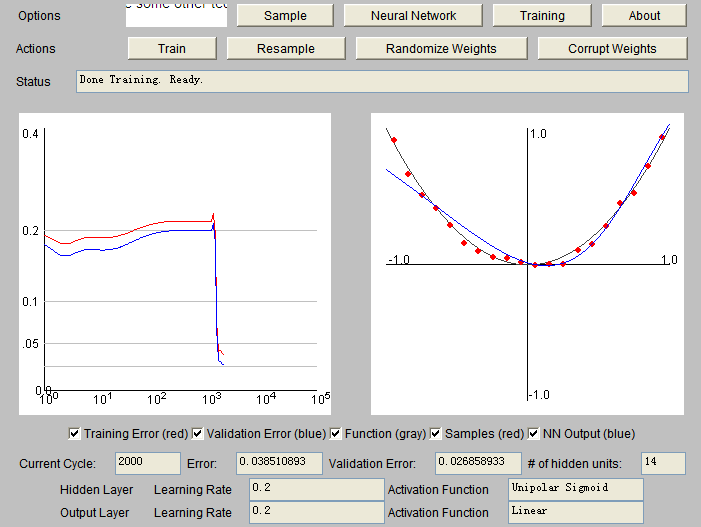
Существуют разные виды масштабирования. Стандартное масштабирование, как вы упомянули, устраняет влияние среднего и стандартного отклонения обучающей выборки, чаще всего используется в машинном обучении. Просто убедитесь, что вы используете то же среднее значение и стандартное значение из обучающей выборки в тестовой выборке.
Причина, по которой требуется масштабирование, заключается в том, что выходные данные сигмоидальной функции находятся в диапазоне (0,1). Я не пробовал, но я думаю, что лучше масштабировать вывод, даже если вы выбираете линейную функцию на выходном слое. В противном случае большой вход на скрытом слое (с сигмоидом) не приведет к значительному выводу (функция сигмоида приблизительно линейна, когда вход находится в небольшом диапазоне, выход за пределы этого диапазона приведет к очень медленному изменению выхода). Вы можете попробовать это самостоятельно в ваших собственных данных.
Кроме того, если у вас есть различные функции, также рекомендуется нормализация функций, которая делает различные функции в одном и том же масштабе. Масштабирование ускоряет снижение градиента, избегая многих дополнительных итераций, которые требуются, когда одна или несколько функций принимают гораздо большие значения, чем остальные.
Как отметил @Ray, глубокое изучение того, что задействовано много уровней функций, может помочь вам в изучении функций, хотя это не все линейные комбинации.