Транспонировать z-положение от перспективы до орфографической камеры в three.js
У меня есть сцена, где я хочу объединить перспективные объекты (т.е. объекты, которые кажутся меньше, когда они находятся далеко) с ортогографическими объектами (то есть, объекты, которые появляются одинакового размера независимо от расстояния). Перспективные объекты являются частью визуализированного "мира", в то время как ортогографические объекты являются украшениями, такими как метки или значки. В отличие от HUD, я хочу, чтобы ортогографические объекты отображались "внутри" мира, что означает, что они могут быть покрыты объектами мира (представьте плоскость, проходящую перед меткой).
Мое решение состоит в том, чтобы использовать один рендер, но две сцены, одна с PerspectiveCamera и один с OrthogographicCamera, Я рендерил их по порядку, не очищая буфер z (рендер autoClear свойство установлено в false). Проблема, с которой я сталкиваюсь, заключается в том, что мне нужно синхронизировать размещение объектов в каждой сцене, чтобы объекту в одной сцене была назначена z-позиция, которая находится позади объектов в другой сцене перед ним, но перед объектами, которые за этим.
Для этого я обозначаю свою перспективную сцену как "ведущую", т.е. все координаты всех объектов (перспективных и ортогональных) назначаются на основе этой сцены. Перспективные объекты используют эти координаты напрямую и отображаются внутри этой сцены и с помощью перспективной камеры. Координаты ортогографических объектов преобразуются в координаты в ортогографической сцене и затем визуализируются в этой сцене с помощью ортогографической камеры. Я выполняю преобразование, проецируя координаты в перспективной сцене на область просмотра перспективной камеры, а затем обратно на ортогональную сцену с помощью ортогографической камеры:
position.project(perspectiveCamera).unproject(orthogographicCamera);
Увы, это не работает с отступом. Ортогографические объекты всегда отображаются перед перспективными объектами, даже если они должны находиться между ними. Рассмотрим пример, в котором синий круг должен отображаться за красным квадратом, но перед зеленым (а это не так):
var pScene = new THREE.Scene();
var oScene = new THREE.Scene();
var pCam = new THREE.PerspectiveCamera(40, window.innerWidth / window.innerHeight, 1, 1000);
pCam.position.set(0, 40, 50);
pCam.lookAt(new THREE.Vector3(0, 0, -50));
var oCam = new THREE.OrthographicCamera(window.innerWidth / -2, window.innerWidth / 2, window.innerHeight / 2, window.innerHeight / -2, 1, 500);
oCam.Position = pCam.position.clone();
pScene.add(pCam);
pScene.add(new THREE.AmbientLight(0xFFFFFF));
oScene.add(oCam);
oScene.add(new THREE.AmbientLight(0xFFFFFF));
var frontPlane = new THREE.Mesh(new THREE.PlaneGeometry(20, 20), new THREE.MeshBasicMaterial( { color: 0x990000 }));
frontPlane.position.z = -50;
pScene.add(frontPlane);
var backPlane = new THREE.Mesh(new THREE.PlaneGeometry(20, 20), new THREE.MeshBasicMaterial( { color: 0x009900 }));
backPlane.position.z = -100;
pScene.add(backPlane);
var circle = new THREE.Mesh(new THREE.CircleGeometry(60, 20), new THREE.MeshBasicMaterial( { color: 0x000099 }));
circle.position.z = -75;
//Transform position from perspective camera to orthogonal camera -> doesn't work, the circle is displayed in front
circle.position.project(pCam).unproject(oCam);
oScene.add(circle);
var renderer = new THREE.WebGLRenderer();
renderer.setSize(window.innerWidth, window.innerHeight);
document.body.appendChild(renderer.domElement);
renderer.autoClear = false;
renderer.render(oScene, oCam);
renderer.render(pScene, pCam);
Вы можете попробовать код здесь.
В перспективном мире (мировое) z-положение круга равно -75, что находится между квадратами (-50 и -100). Но это на самом деле отображается перед обоими квадратами. Если вы вручную установите z-положение окружностей (в ортогографической сцене) на -500, оно будет отображаться между квадратами, поэтому при правильном расположении то, что я пытаюсь сделать, должно быть возможным в принципе.
Я знаю, что не могу визуализировать сцену одинаково с ортогональными и перспективными камерами Мое намерение состоит в том, чтобы перед каждым рендерингом переместить все ортогональные объекты, чтобы они оказались в правильном положении
Что мне нужно сделать, чтобы рассчитать ортогографические координаты по координатам перспективы, чтобы объекты отображались с правильными значениями глубины?
ОБНОВИТЬ:
Я добавил ответ с моим текущим решением проблемы на случай, если у кого-то возникнет аналогичная проблема. Однако, поскольку это решение не обеспечивает такое же качество, как у ортогографической камеры. Так что я все равно был бы рад, если бы кто-нибудь смог объяснить, почему ортогографическая камера не работает должным образом и / или предоставить решение проблемы.
2 ответа
Вы очень близки к результату, который вы ожидали. Вы забыли обновить матрицы камеры, для которых необходимо рассчитать, что операция project а также project может правильно работать:
pCam.updateMatrixWorld ( false );
oCam.updateMatrixWorld ( false );
circle.position.project(pCam).unproject(oCam);
Объяснение:
При рендеринге каждая сетка сцены обычно преобразуется матрицей модели, матрицей вида и матрицей проекции.
Матрица проекции:
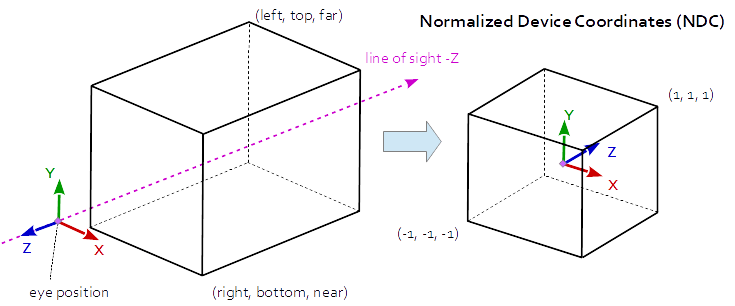
Матрица проекции описывает отображение от трехмерных точек сцены к двухмерным точкам области просмотра. Матрица проекции преобразуется из пространства просмотра в пространство клипа, а координаты в пространстве клипа преобразуются в нормализованные координаты устройства (NDC) в диапазоне (-1, -1, -1) в (1, 1, 1) путем деления с компонентом w координат клипа.Посмотреть матрицу:
Матрица вида описывает направление и позицию, с которой просматривается сцена. Матрица вида трансформируется из пространства Вольда в пространство вида (глаза). В системе координат в окне просмотра ось X указывает влево, ось Y вверх и ось Z находятся вне вида (обратите внимание, что в правой системе Z-ось является перекрестным произведением X-оси). Ось и ось Y).Модельная матрица:
Матрица модели определяет местоположение, ориентацию и относительный размер сетки в сцене. Матрица модели преобразует позиции вершин из сетки в мировое пространство.
Если фрагмент нарисован "позади" или "перед" другим фрагментом, зависит от значения глубины фрагмента. В то время как для ортографической проекции координата Z пространства вида линейно отображается на значение глубины, в перспективной проекции она не является линейной.
В общем случае значение глубины рассчитывается следующим образом:
float ndc_depth = clip_space_pos.z / clip_space_pos.w;
float depth = (((farZ-nearZ) * ndc_depth) + nearZ + farZ) / 2.0;
Матрица проекции описывает отображение от трехмерных точек сцены к двухмерным точкам области просмотра. Он преобразуется из пространства глаза в пространство клипа, а координаты в пространстве клипа преобразуются в нормализованные координаты устройства (NDC) путем деления на компонент w координат клипа.
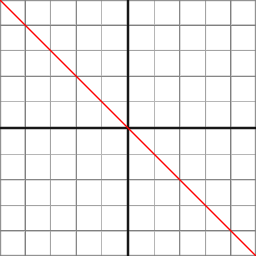
В ортогональной проекции координаты в глазном пространстве линейно отображаются на нормализованные координаты устройства.
Ортографическая проекция
В ортогональной проекции координаты в глазном пространстве линейно отображаются на нормализованные координаты устройства.
Ортографическая матрица проекции:
r = right, l = left, b = bottom, t = top, n = near, f = far
2/(r-l) 0 0 0
0 2/(t-b) 0 0
0 0 -2/(f-n) 0
-(r+l)/(r-l) -(t+b)/(t-b) -(f+n)/(f-n) 1
В ортогональной проекции Z-компонент вычисляется линейной функцией:
z_ndc = z_eye * -2/(f-n) - (f+n)/(f-n)
Перспективная проекция
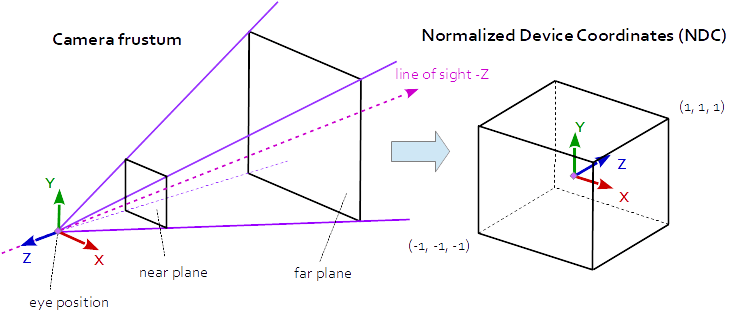
В перспективной проекции матрица проекции описывает отображение из трехмерных точек в мире, как они видны с камеры-обскуры, в двумерные точки видового экрана.
Координаты пространства глаза в усеченной области камеры (усеченная пирамида) отображаются в куб (нормализованные координаты устройства).
Матрица перспективной проекции:
r = right, l = left, b = bottom, t = top, n = near, f = far
2*n/(r-l) 0 0 0
0 2*n/(t-b) 0 0
(r+l)/(r-l) (t+b)/(t-b) -(f+n)/(f-n) -1
0 0 -2*f*n/(f-n) 0
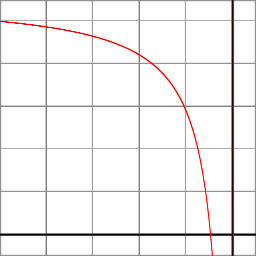
В перспективной проекции Z-компонент вычисляется рациональной функцией:
z_ndc = ( -z_eye * (f+n)/(f-n) - 2*f*n/(f-n) ) / -z_eye
Подробное описание смотрите в ответе на вопрос о переполнении стека. Как визуализировать глубину линейно в современном OpenGL с gl_FragCoord.z во фрагментном шейдере?
В вашем случае это означает, что вы должны выбрать координату Z круга в ортографической проекции таким образом, чтобы значение глубины находилось между глубинами объектов в перспективной проекции.
Так как значение глубины не более чем depth = z ndc * 0.5 + 0.5 в обоих случаях можно также выполнять вычисления по нормализованным координатам устройства вместо значений глубины.
Нормализованные координаты устройства могут быть легко вычислены project функция THREE.PerspectiveCamera, project преобразует из пространства wolrd в пространство просмотра и из пространства просмотра в нормализованные координаты устройства.
Чтобы найти координату Z, которая находится между ними в ортографической проекции, среднюю нормализованную координату Z устройства необходимо преобразовать в координату Z пространства обзора. Это может быть сделано unproject функция THREE.PerspectiveCamera, unproject преобразует из нормализованных координат устройства для просмотра пространства и из пространства просмотра в пространство мира.
Смотрите далее OpenGL - Координаты мыши в Космические координаты.
Смотрите пример:
var renderer, pScene, oScene, pCam, oCam, frontPlane, backPlane, circle;
var init = function () {
pScene = new THREE.Scene();
oScene = new THREE.Scene();
pCam = new THREE.PerspectiveCamera(40, window.innerWidth / window.innerHeight, 1, 1000);
pCam.position.set(0, 40, 50);
pCam.lookAt(new THREE.Vector3(0, 0, -50));
oCam = new THREE.OrthographicCamera(window.innerWidth / -2, window.innerWidth / 2, window.innerHeight / 2, window.innerHeight / -2, 1, 500);
oCam.Position = pCam.position.clone();
pScene.add(pCam);
pScene.add(new THREE.AmbientLight(0xFFFFFF));
oScene.add(oCam);
oScene.add(new THREE.AmbientLight(0xFFFFFF));
frontPlane = new THREE.Mesh(new THREE.PlaneGeometry(20, 20), new THREE.MeshBasicMaterial( { color: 0x990000 }));
frontPlane.position.z = -50;
pScene.add(frontPlane);
backPlane = new THREE.Mesh(new THREE.PlaneGeometry(20, 20), new THREE.MeshBasicMaterial( { color: 0x009900 }));
backPlane.position.z = -100;
pScene.add(backPlane);
circle = new THREE.Mesh(new THREE.CircleGeometry(20, 20), new THREE.MeshBasicMaterial( { color: 0x000099 }));
circle.position.z = -75;
//Transform position from perspective camera to orthogonal camera -> doesn't work, the circle is displayed in front
pCam.updateMatrixWorld ( false );
oCam.updateMatrixWorld ( false );
circle.position.project(pCam).unproject(oCam);
oScene.add(circle);
renderer = new THREE.WebGLRenderer();
renderer.setSize(window.innerWidth, window.innerHeight);
document.body.appendChild(renderer.domElement);
};
var render = function () {
renderer.autoClear = false;
renderer.render(oScene, oCam);
renderer.render(pScene, pCam);
};
var animate = function () {
requestAnimationFrame(animate);
//controls.update();
render();
};
init();
animate();html,body {
height: 100%;
width: 100%;
margin: 0;
overflow: hidden;
}<script src="https://threejs.org/build/three.min.js"></script>Я нашел решение, которое включает в себя только перспективную камеру и масштабирует украшения в соответствии с их расстоянием до камеры. Это похоже на ответ на аналогичный вопрос, но не совсем то же самое. Моя конкретная проблема заключается в том, что мне нужно, чтобы украшения не были одинакового размера, независимо от их расстояния до камеры, мне также нужно контролировать их точный размер на экране.
Чтобы масштабировать их до нужного размера, а не до любого размера, чтобы доза не изменилась, я использую функцию для расчета размера экрана, найденного в этом ответе, чтобы вычислить положение обоих концов вектора известной длины на экране и проверить длина проекции на экран. Из разницы в длине я могу рассчитать точный коэффициент масштабирования:
var widthVector = new THREE.Vector3( 100, 0, 0 );
widthVector.applyEuler(pCam.rotation);
var baseX = getScreenPosition(circle, pCam).x;
circle.position.add(widthVector);
var referenceX = getScreenPosition(circle, pCam).x;
circle.position.sub(widthVector);
var scale = 100 / (referenceX - baseX);
circle.scale.set(scale, scale, scale);
Проблема с этим решением состоит в том, что в большинстве случаев расчет является достаточно точным, чтобы обеспечить точный размер. Но время от времени некоторые ошибки округления приводят к тому, что украшение отображается неправильно.