Могу ли я переключить X Y Z в кватернионе?

Question

У меня есть система координат, где ось Y вверх. Мне нужно преобразовать его в систему координат, где Z вверх. У меня есть вращения, хранящиеся в кватернионах, поэтому мой вопрос: если у меня есть кватернион X,Y,Z, могу ли я поменять Y на Z и получить результат, что Z действительно UP?

Answer 1

Просто поменять две оси в кватернионах? Нет, это не работает, потому что это переворачивает хиральность. Однако, если вы перевернете киральность и отрицаете реальную часть кватерниона, тогда вы вернетесь к первоначальной хиральности. В общем виде вы можете написать это как

Q '(Q, i'j'k') = ε_{i'j'k '} Q_w_w + Q_i_i + Q_j_j + Q_k_k

где

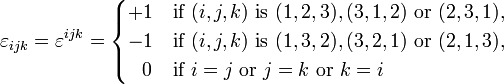
является полностью антисимметричным тензором, известным как символ Леви-Кевита.

Это не должно быть сюрпризом, поскольку правила кватернионов i², j², k² определяются также одним и тем же полностью антисимметричным тензором.

Answer 2

Я адаптирую свой ответ из этого поста, поскольку тот, что здесь, был более старым и, вероятно, более общим.

Вероятно, лучше всего рассмотреть это в контексте того, как вы преобразуете угол и ось в кватернион. В Википедии вы можете прочитать, что вы описываете вращение на угол вокруг оси с единичным вектором направления (x,y,z), используя

q = cos(θ/2) + sin(θ/2)(xi + yj + zk)

Ваш пост говорит нам только Y ↦ Z, то есть старое направление Y - это новое направление Z. А как насчет других направлений? Вы, вероятно, хотите сохранить X ↦ X, но это все еще оставляет нам две альтернативы.

1. Либо вы используете Z ↦ Y. В этом случае вы переключаетесь между левой и правой системами координат, и преобразование по сути является отражением.
2. Или вы используете Z ↦ −Y, тогда это просто поворот на 90° вокруг оси X. Ручность системы координат остается прежней.

Смена хиральности

Рассматривая первый случай первым. Что делает изменение системы координат для вашего угла и оси? Ну, координаты оси меняются так же, как и ваши точки, и угол меняет знак. Так что у тебя есть

cos(−θ/2) + sin(−θ/2)(xi + zj + yk)

По сравнению с вышеизложенным действительная часть не изменяется (поскольку cos (x) = cos (-x)), но мнимые части изменяют свой знак, в дополнение к изменению порядка. Обобщая из этого, кватернион a + bi + cj + dk описание вращения в старой системе координат будет превращено в a − bi − dj − ck в новой системе координат. Или в −a + bi + dj + ck это другое описание того же вращения (так как оно меняет θ на 360°, но θ / 2 на 180°).

Сохраненная хиральность

По сравнению с этим во втором случае Z ↦ −Y сохраняет знак θ, поэтому вам нужно только отрегулировать ось. Новая координата Z является старой координатой Y, а новая координата Y является отрицательной старой координатой Z. Так a + bi + cj + dk превращается в a + bi − dj + ck (или его негатив). Обратите внимание, что это просто умножение кватерниона на i или же −iв зависимости от того, с какой стороны вы умножаете его. Если вы хотите записать это как сопряжение, у вас θ=±45°, так что вы получите квадратные корни в кватернионе, который выражает изменение системы координат.

Answer 3

Попробуйте: вращение кватерниона = новый кватернион (X,Z,Y, -W); // мне пришлось поменять местами Z и Y из-за

Answer 4

Нет, вы не можете поменять y и z - он превратится в левостороннюю систему координат, если она была правосторонней (и наоборот).

Однако вы можете сделать следующую замену:

newX = oldZ
newY = oldX
newZ = oldY

Я подозреваю, что вам действительно нужно простое вращение вокруг оси x. Если именно поэтому вы хотите переключить y и z, вам следует вместо этого применить вращение на -90 градусов вокруг оси +x (при условии, что у вас есть правосторонняя система координат).