Генерация гексагональной решетки с помощью Spatstat

Question

Я анализирую схему роста определенных частиц и хочу сравнить точечный рисунок с идеально шестиугольной решеткой с той же интенсивностью (одинаковое количество точек на единицу площади). Я написал функцию, которая делает это, но в ней есть внутренняя ошибка, и я не уверен, откуда она возникла. По сути, после того, как функция прошла свой ход, она выдает идеально шестиугольный точечный рисунок, который НЕ имеет правильного числа частиц - обычно он отключается примерно на 1-4%. Если вы скопируете и вставите следующий код в R, вы увидите это - в этом конкретном примере ошибка составляет 11,25% - исходный точечный шаблон содержит 71 частицу, а сгенерированный идеально шестиугольный точечный шаблон имеет 80 частиц. Это кажется очень странным, поскольку код, как вы увидите, предназначен для размещения частиц на определенном расстоянии друг от друга, тем самым создавая окно того же размера, что и оригинал, с тем же числом частиц.

Ниже приведен код функции, которую я написал для генерации гексагональной решетки.

library(spatstat)

data(swedishpines)

swedishpines.df <- as.data.frame(swedishpines)

MaxXValue <- max(swedishpines.df[1])
MaxYValue <- max(swedishpines.df[2])
#The above two lines dictate the window size
NumberOfParticles <- nrow(swedishpines.df[1])
#Number of entries = number of particles

#calculate delta
intensity <- NumberOfParticles / (MaxXValue*MaxYValue)
#Intensity ---> particles / unit^2
    #Area = ( sqrt(3) / 2 ) * delta^2
    #Now - in substituting intensity in for area, it is key to recognize 
    #that there are 3 particles associated with each hexagonal tile.
    #This is because each particle on the border of the tile is really 1/3 of a 
    #a particle due to it being associated with 3 different hexagonal tiles.  
    #Since intensity = 3 Particles / Area, 
delta <- sqrt(2/(intensity*(sqrt(3))))
#This is derived from the equation for the area of a regular hexagon. 

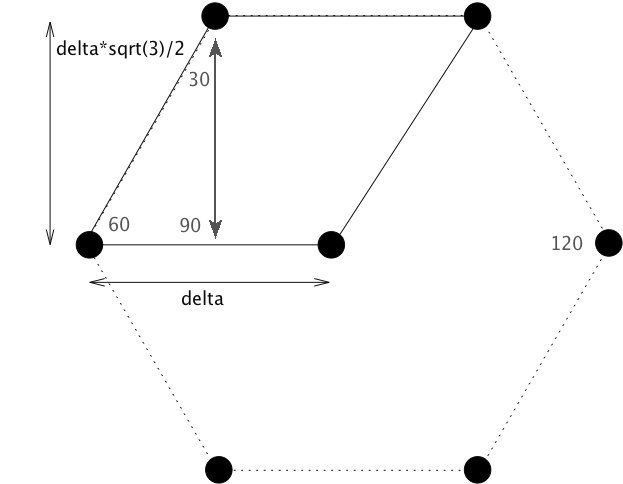
#xcoords and ycoords represent the x and y coordintes of all of the generated points.  The 'x' and 'y' are temporary holders for the x and y coordinates of a single horizontal line of points (they are appended to xcoords and ycoords at the end of each while loop).  

xcoords <- c()
ycoords <- c()

#The following large while loop calculates the coordinates of the first set of points that are vertically aligned with one another. (alternating horizontal lines of particles)  This is shown in the image below.

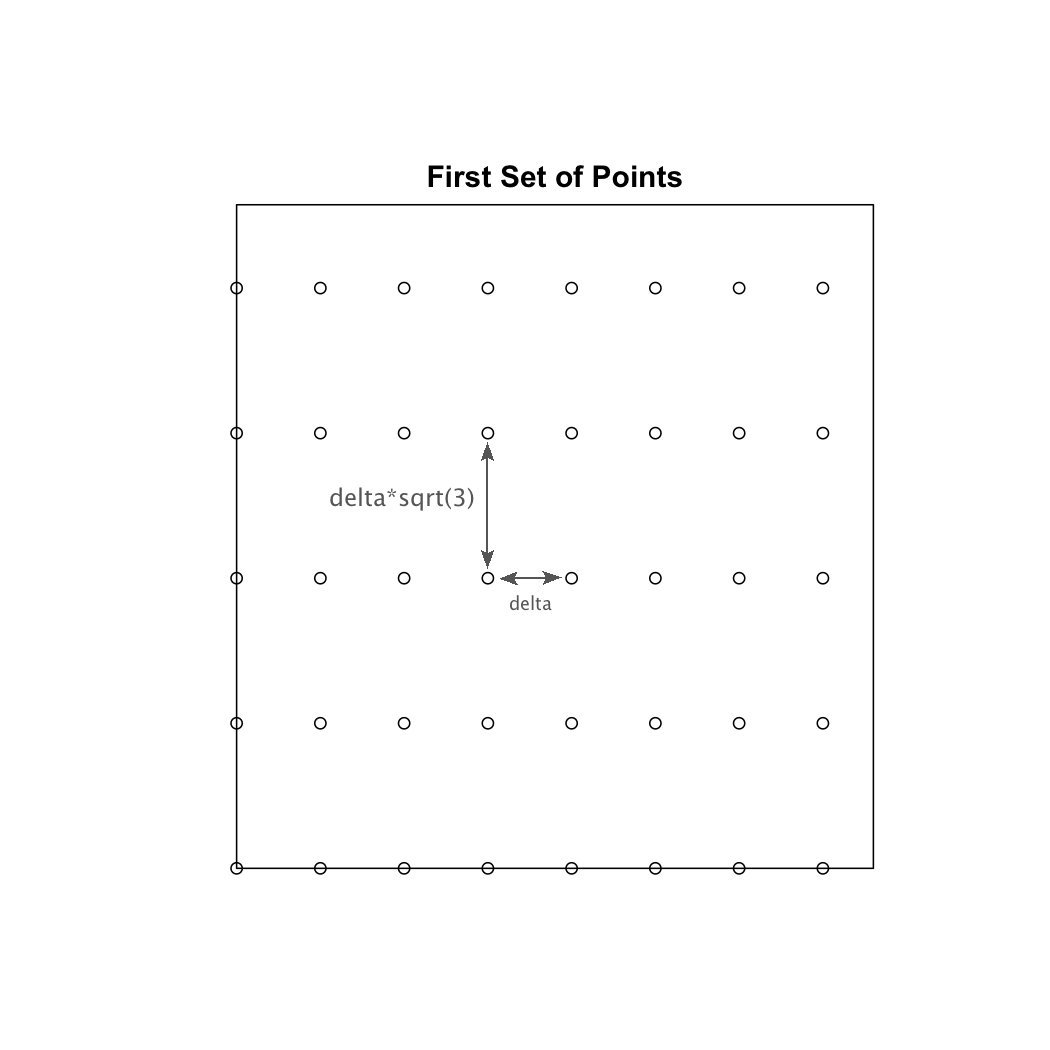
y_shift <- 0
while (y_shift < MaxYValue) {

    x <- c(0)
    x_shift <- 0 + delta
    count <- 0

    while (x_shift < MaxXValue) {
        x <- append(x, x_shift)
        x_shift <- x_shift + delta
        count <- count + 1
    }

    y <- c(y_shift)

    for (i in seq(0,(count-1))) {
        y <- append(y, y_shift)
    }

    y_shift <- y_shift + sqrt(3)*delta
    xcoords <- append(xcoords,x)
    ycoords <- append(ycoords,y)

}

#The following large while loop calculates the coordinates of the second set of points that are vertically aligned with one another. This is shown in the image below. 

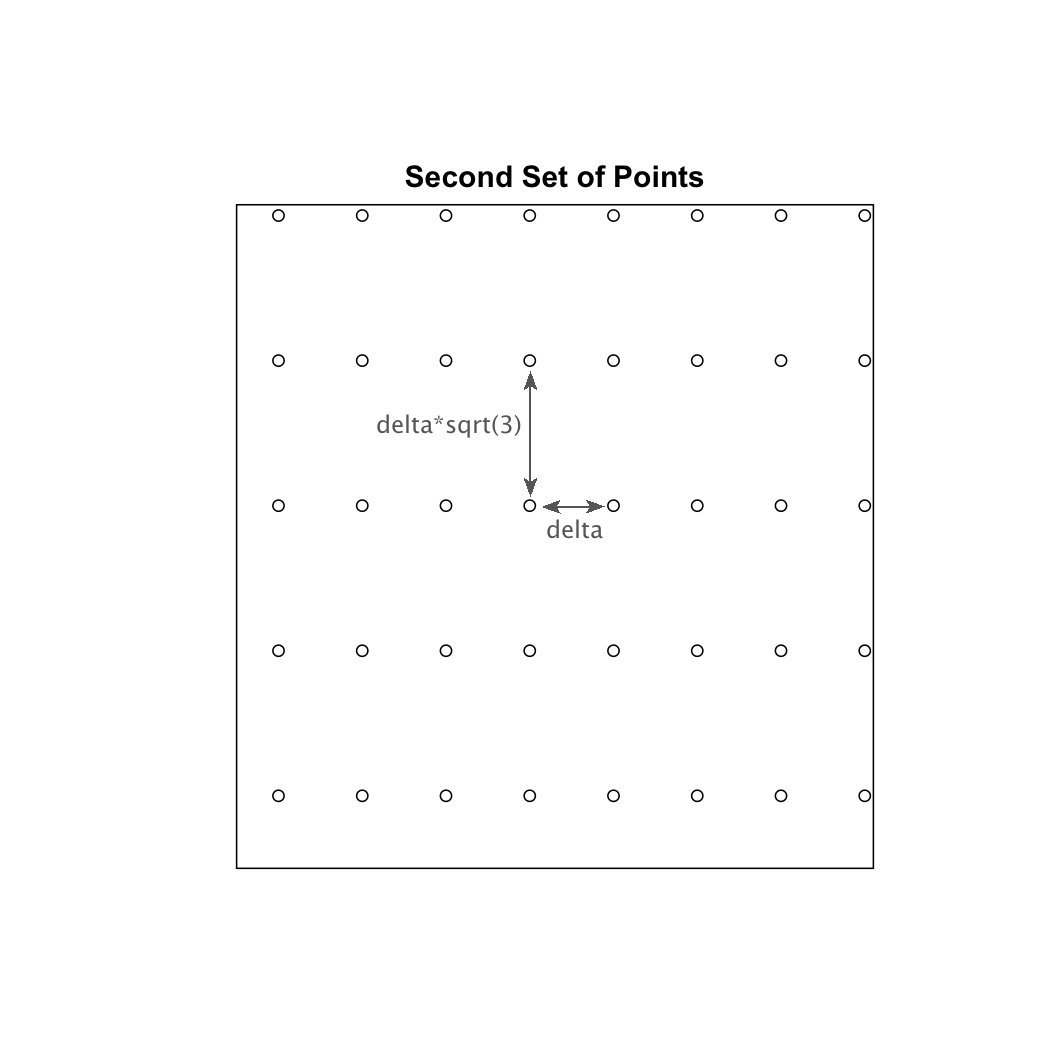
y_shift <- 0 + (delta*(sqrt(3)))/2
while (y_shift < MaxYValue) {

    x <- c(0 + (1/2)*delta)
    x_shift <- 0 + (1/2)*delta + delta
    count <- 0

    while (x_shift < MaxXValue) {
        x <- append(x, x_shift)
        x_shift <- x_shift + delta
        count <- count + 1
    }

    y <- c(y_shift)

    for (i in seq(0,(count-1))) {
        y <- append(y, y_shift)
    }

    y_shift <- y_shift + sqrt(3)*delta
    xcoords <- append(xcoords,x)
    ycoords <- append(ycoords,y)

}

hexplot <- ppp(xcoords, ycoords, window=owin(c(0,MaxXValue),c(0,MaxYValue)))

Теперь я относительно новичок в R, так что это может быть синтаксическая ошибка где-то в коде, которая вызвала эту ошибку. Или, может быть, у меня есть какая-то ошибка в моей мысли с этим процессом. Тем не менее, я не думаю, что это вероятно, так как мои результаты были довольно близки к тому, что я пытался (только ошибка 1-4% в большинстве случаев довольно хорошая).

Таким образом, я хотел бы помочь, как взять точечный узор и создать еще один точечный узор того же размера окна с тем же количеством частиц, но идеально гексагональной точечный узор.

Пожалуйста, не стесняйтесь просить меня объяснить что-нибудь, если вы чувствуете, что что-то неясно.

Спасибо!

Answer 1

Простите, если я ошибаюсь, но я считаю, что то, что вы пытаетесь сделать, невозможно (в общем случае), учитывая ограничения, которые вы показали в примере. Проще говоря, можете ли вы придумать способ нарисовать 71 точку в шестиугольнике на странице с той же высотой и шириной, что и у вашего окна? Я не думаю, что такая модель существует.

Чтобы объяснить далее, рассмотрим последнюю строку в вашем коде:

hexplot <- ppp(xcoords, ycoords, window=owin(c(0,MaxXValue),c(0,MaxYValue)))

Теперь, поскольку ваше окно имеет тот же размер, что и исходные данные, чтобы получить ту же интенсивность, вам потребуется ровно столько же точек (71). В вашем расположении точек шестиугольника у вас есть x строк, каждая из которых содержит y точек. Но нет целых чисел x и y, которые умножаются на 71.

При этом, если вы немного "растянете" ширину окна, то половина ваших строк будет содержать еще одну точку. Это более слабое ограничение, но нет гарантии, что в общем случае будет решение.

Таким образом, чтобы получить точно такую ​​же интенсивность точек, вам нужно будет изменить относительный размер окна. Вам нужно будет растянуть его, чтобы добавить пробел и получить более низкую интенсивность точки. Это все еще может не сработать в общем случае... но, может быть, я не сработал. Возможно, проще всего начать с простой сетки, а затем развернуть код до шестиугольников.

---

Глядя на ваш код, я заметил, что вы используете while петли, когда вы могли бы использовать seq функция. Например, если вы хотите сгенерировать все x указывает от 0 до MaxXValue увеличивается на sqrt(3)*deltaПросто сделайте:

x<-seq(0,MaxXValue,by=delta)

вместо этого большого while, Здесь могут быть некоторые ошибки, но я думаю, что вы можете сократить весь код до:

library(spatstat)
data(swedishpines)
swedishpines.df <- as.data.frame(swedishpines)
MaxXValue <- max(swedishpines.df[1])
MaxYValue <- max(swedishpines.df[2])
NumberOfParticles <- nrow(swedishpines.df)
intensity <- NumberOfParticles / (MaxXValue*MaxYValue)
delta <- sqrt(2/(intensity*(sqrt(3))))
x<-seq(0,MaxXValue,by=delta)
y<-seq(0,MaxYValue,by=sqrt(3)*delta)
first.coords=merge(x,y) # Find every combo of x and y
x=seq(delta/2,MaxXValue,by=delta)
y=delta*sqrt(3)/2 + (delta*sqrt(3)*seq(0,length(x)/2))
second.coords=merge(x,y)
coords=rbind(first.coords,second.coords)
ppp(coords$x, coords$y, window=owin(c(0,MaxXValue),c(0,MaxYValue)))

Наконец, я заметил в ваших комментариях, что вы упоминаете, что площадь шестиугольника ( sqrt(3) / 2 ) * delta^2но не так ли (3*sqrt(3)/2) * delta^2? `

---

Меня заинтересовал комментарий Джоша О'Брайена, и я решил реализовать функцию поворота, чтобы получить точное количество желаемых баллов. Вот код:

# Include all above code
rotate=function(deg) {
    r=matrix(c(cos(deg),-sin(deg),sin(deg),cos(deg)),byrow=T,nrow=2)
    rotated.coords=data.frame(t(r %*% t(as.matrix(coords))))
    names(rotated.coords)=c('x','y')
    rotated.coords
}

rotate.optim=function(deg) {
    rotated.coords=rotate(deg)
    abs(NumberOfParticles-length(suppressWarnings(ppp(rotated.coords$x, rotated.coords$y, window=owin(c(0,MaxXValue),c(0,MaxYValue)))$x)))
}

o=optim(0,rotate.optim,lower=0,upper=2*pi,method='Brent')
rotated.coords=rotate(o$par)
rotated.coords.window=rotated.coords[rotated.coords$x >= 0 & rotated.coords$y >= 0 & rotated.coords$x <= MaxXValue & rotated.coords$y <= MaxYValue,]
final=ppp(rotated.coords.window$x,rotated.coords.window$y,window=owin(c(0,MaxXValue),c(0,MaxYValue)))
plot(final)

Answer 2

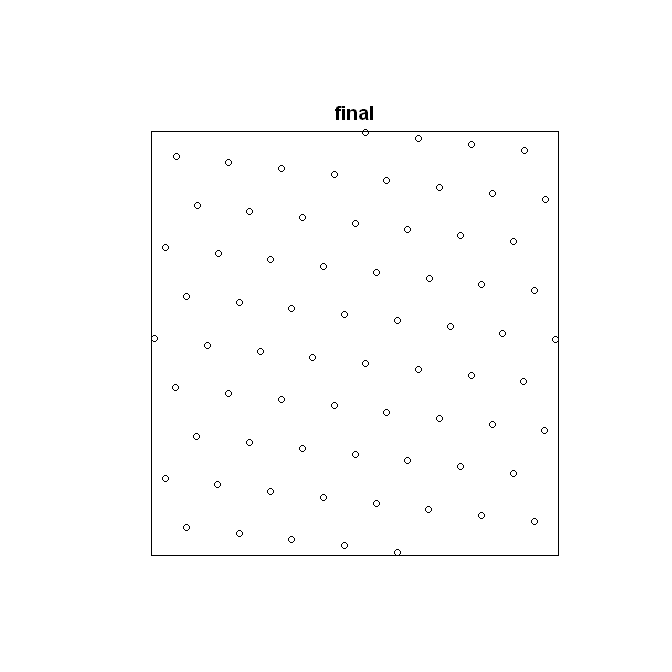
Просто для полноты добавлю, что у spatstat теперь есть функция hexgrid генерировать гексагональную сетку, и есть rotate.ppp который мог быть применен впоследствии, чтобы вращать образец.