Координаты OpenGL из кривых Безье
По сути, мне нужно получить все координаты, нарисованные из реализации кривой Безье в OpenGL. В частности, мне нужны координаты для перемещения сферического объекта (бейсбол) в моей сцене по кривой траектории. Это то, что я использую, чтобы нарисовать мою кривую:
GL2 gl = drawable.getGL().getGL2();
float ctrlpoints[][] = new float[][]{
{0.0f, 0.0f, 60f},
{0.0f, 3.0f, 45.0f},
{0.0f, 2.0f, 15.0f},
{0.0f, 1.0f, 0f}};
FloatBuffer ctrlpointBuf = FloatBuffer.allocate(ctrlpoints[0].length * ctrlpoints.length);
for (int i = 0; i < ctrlpoints.length; i++) {
for (int j = 0; j < 3; j++) {
ctrlpointBuf.put(ctrlpoints[i][j]);
}
}
ctrlpointBuf.rewind();
gl.glMap1f(GL2.GL_MAP1_VERTEX_3, 0.0f, 1.0f, 3, numControlPoints, ctrlpointBuf);
gl.glEnable(GL2.GL_MAP1_VERTEX_3);
gl.glColor3f(1.0f, 1.0f, 1.0f);
gl.glBegin(GL2.GL_LINE_STRIP);
for (int i = 0; i <= 30; i++) {
gl.glEvalCoord1f((float) i / (float) 30.0);
}
gl.glEnd();
Кто-нибудь знает, как получить очки из этой реализации?
5 ответов
Кривая Безье довольно проста для вычисления. Прежде всего, является отделимым, это означает, что вы можете вычислить его по одной координате за раз (сначала x, затем y, затем z...). Для данной координаты следующая функция, которая использует определение:
double bezier(double A, // Start value
double B, // First control value
double C, // Second control value
double D, // Ending value
double t) // Parameter 0 <= t <= 1
{
double s = 1 - t;
double AB = A*s + B*t;
double BC = B*s + C*t;
double CD = C*s + D*t;
double ABC = AB*s + BC*t;
double BCD = BC*s + CD*t;
return ABC*s + BCD*t;
}
Обратите внимание, что в приведенной выше функции параметр t это не параметр длины дуги для кривой, а общий параметр, который идет от t=0 (где точка находится в начале кривой) t=1 (где точка находится в конце кривой).
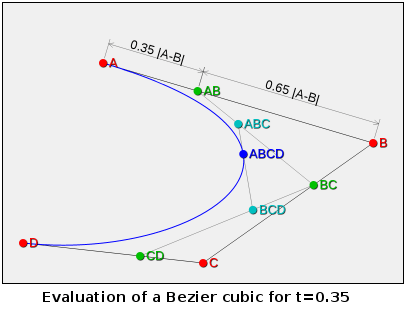
Интерактивная версия рисунка выше, где вы можете перетаскивать точки A, B, C, D и A B, доступна здесь. Он реализован с использованием html/js/canvas и протестирован только в Chrome, Firefox, Safari.
Если вам нужно перемещать объекты с управляемой определенной скоростью в XYZ, то простым способом является вычисление аппроксимированной полилинии (например, путем выборки кривой для 100 значений t), а затем идти с постоянной скоростью по получившейся полилинии.
Истинная параметризация длины дуги для кубики Безье (т. Е. С использованием параметра, который является длиной, измеренной вдоль кривой) является довольно раздражающей для вычисления (IIRC не имеет решения для замкнутой формы для интеграла).
Я думаю, что следующая строка в Bezier() должна читать
двойной ABC = AB*s + CD*t;
вместо
двойной ABC = BC*s + CD*t;
Быстрый тест с программой.c дает такие результаты. Обратите внимание, что координаты кривой начинаются в 10.00 вместо 20.00 с указанной выше неизмененной функцией.
~/sujith/cc > gcc oglBezier.c
~/sujith/cc > ./a.out
Start. A=10.000000, B=20.000000, C=40.000000, D=5.000000, t=0.000000
Bezier pt= 10.000000
Bezier pt= 10.495490
Bezier pt= 10.981920
Bezier pt= 11.459230
Bezier pt= 11.927360
Bezier pt= 12.386250
Bezier pt= 12.835840
Bezier pt= 13.276070
Bezier pt= 13.706880
Bezier pt= 14.128210
Bezier pt= 14.540000
Bezier pt= 14.942190
Bezier pt= 15.334720
Bezier pt= 15.717530
Bezier pt= 16.090560
Bezier pt= 16.453750
Bezier pt= 16.807040
Bezier pt= 17.150370
Bezier pt= 17.483680
Bezier pt= 17.806910
Bezier pt= 18.120000
Bezier pt= 18.422890
Bezier pt= 18.715520
Bezier pt= 18.997830
Bezier pt= 19.269760
Bezier pt= 19.531250
Bezier pt= 19.782240
Bezier pt= 20.022670
Bezier pt= 20.252480
Bezier pt= 20.471610
Bezier pt= 20.680000
Bezier pt= 20.877590
Bezier pt= 21.064320
Bezier pt= 21.240130
Bezier pt= 21.404960
Bezier pt= 21.558750
Bezier pt= 21.701440
Bezier pt= 21.832970
Bezier pt= 21.953280
Bezier pt= 22.062310
Bezier pt= 22.160000
Bezier pt= 22.246290
Bezier pt= 22.321120
Bezier pt= 22.384430
Bezier pt= 22.436160
Bezier pt= 22.476250
Bezier pt= 22.504640
Bezier pt= 22.521270
Bezier pt= 22.526080
Bezier pt= 22.519010
Bezier pt= 22.500000
Bezier pt= 22.468990
Bezier pt= 22.425920
Bezier pt= 22.370730
Bezier pt= 22.303360
Bezier pt= 22.223750
Bezier pt= 22.131840
Bezier pt= 22.027570
Bezier pt= 21.910880
Bezier pt= 21.781710
Bezier pt= 21.640000
Bezier pt= 21.485690
Bezier pt= 21.318720
Bezier pt= 21.139030
Bezier pt= 20.946560
Bezier pt= 20.741250
Bezier pt= 20.523040
Bezier pt= 20.291870
Bezier pt= 20.047680
Bezier pt= 19.790410
Bezier pt= 19.520000
Bezier pt= 19.236390
Bezier pt= 18.939520
Bezier pt= 18.629331
Bezier pt= 18.305761
Bezier pt= 17.968751
Bezier pt= 17.618241
Bezier pt= 17.254171
Bezier pt= 16.876481
Bezier pt= 16.485111
Bezier pt= 16.080001
Bezier pt= 15.661091
Bezier pt= 15.228321
Bezier pt= 14.781631
Bezier pt= 14.320961
Bezier pt= 13.846251
Bezier pt= 13.357441
Bezier pt= 12.854471
Bezier pt= 12.337281
Bezier pt= 11.805811
Bezier pt= 11.260001
Bezier pt= 10.699791
Bezier pt= 10.125121
Bezier pt= 9.535931
Bezier pt= 8.932161
Bezier pt= 8.313751
Bezier pt= 7.680641
Bezier pt= 7.032771
Bezier pt= 6.370081
Bezier pt= 5.692512
Bezier pt= 5.000002
Тестовая программа oglBezier.c:
#include <stdio.h>
double bezier(double A, // Start value
double B, // First control value
double C, // Second control value
double D, // Ending value
double t) // Parameter 0 <= t <= 1
{
double s = 1 - t;
double AB = A*s + B*t;
double BC = B*s + C*t;
double CD = C*s + D*t;
double ABC = AB*s + CD*t;
double BCD = BC*s + CD*t;
return ABC*s + BCD*t;
}
main()
{
double a,b,c,d,t;
a = 10.0f;
b = 20.0f;
c = 40.0f;
d = 5.0f;
t = 0.0f;
printf("Start. A=%f, B=%f, C=%f, D=%f, t=%f\n", a,b,c,d,t);
while(1)
{
if(t>1.0f)
break;
printf("Bezier pt= %f\n", bezier(a,b,c,d,t));
t += 0.01f;
}
return 1;
}
В случае, если кому-то интересно, вот как я наконец реализовал распределение сферы бейсбола в моей сцене, используя траекторию, нарисованную кривой Безье. Я использовал очень яркую функцию 6502 для вычисления координат XYZ для шара в каждом кадре. Начальное значение - где шар находится на кривой во время рисования рамки. Конечное значение и контрольные точки одинаковы для рисования всей кривой. Мне потребовалось некоторое время, чтобы выяснить, какие аргументы приводить для параметра t.
Я наконец понял, что это были значения от 0, НАЧАЛО кривой, до 1, КОНЕЦ кривой. Таким образом, бейсбольный мяч, разбитый от насыпи кувшинов, будет t=0 в 60,5 футах от домашней плиты и t=1 в 0 футах от домашней плиты. Таким образом, т может быть вычислено так же просто, как
t += 1.0 / 60.5;
Сначала я нарисовал всю кривую как GL_LINE_STRIP, а затем вычислил координаты шара в каждом кадре. Когда я запускал свою программу, мяч точно следовал траектории кривой линии. Спасибо всем, кто дал ответы и сделал комментарии.
Я взял формулу, исправил ее и создал тестовое приложение на github на git://github.com/rmd6502/BezierLicious.git . Я настоятельно рекомендую не использовать все, что я там делал, в производственном приложении - рассматривайте это только для исследовательских целей!!
Вы должны взглянуть на алгоритм де Кастельжау. Это позволяет рекурсивно уточнить вашу кривую. Просто прервите выполнение после нескольких шагов и используйте полученные вершины. Вы также можете оценить контрольные точки непосредственно вдоль параметрической позиции и использовать их. Нетрудно напрямую оценить безье-сплайны (например, вы можете сделать это в вершинном шейдере!) Преимущество алгоритма де Кастельжау состоит в том, что вам никогда не придется вычислять (высокие) степени, хотя для вашего случая оба должны быть хорошими (и прямая оценка определенно легче осуществить / протестировать.)