Как я могу генерировать гауссовский случайный процесс, используя Matlab?
Как я могу генерировать гауссовский случайный процесс, используя Matlab с нулевым средним и единичной дисперсией?
Гауссова случайная величина может быть реализована
W =(1/ SQRT (2* пи))* ехр (-(т ^2)/2.);
а как насчет гауссовского случайного процесса?
2 ответа
Если гауссовский процесс белый (нет корреляции между выборками в разные моменты времени), просто используйте
w = randn(1,n);
где n желаемое количество образцов.
Если вам необходимо ввести корреляцию между выборками (то есть значения в разные моменты времени коррелируются), обычный подход состоит в том, чтобы сгенерировать белый гауссовский процесс, а затем применить фильтр нижних частот (используя conv или же filter). Автокорреляция процесса определяется формой фильтра.
Например,
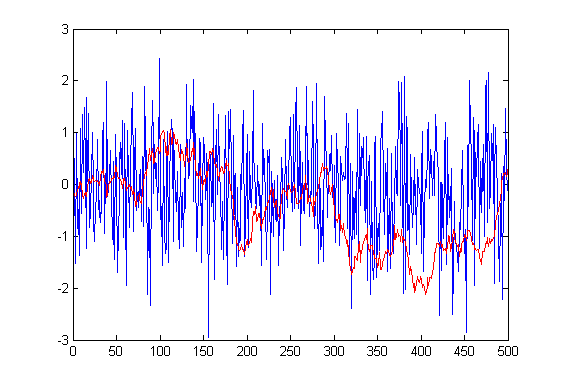
w = randn(1,500);
y = conv(w,ones(1,100)/10,'same'); %// apply a simple low-pass filter
plot(w)
hold on
plot(y,'r')
Вы можете видеть, что отфильтрованный сигнал (красный) имеет более плавные изменения во времени из-за (авто) корреляции, введенной фильтром.
Случайный процесс Гаусса с заданной длиной корреляции (cl) и среднеквадратичной высотой (hRMSE) может быть сгенерирован путем пропускания белого шума со средним 0 и стандартным отклонением hRMSE через гауссов фильтр g=exp(-(x.^2)/(cl^2/2)),
Кроме того, вы можете найти код Matlab по ссылке ниже: http://www.mysimlabs.com/matlab/surfgen/rsgeng1D.m
Который был расшифрован ниже:
function [f,x] = rsgeng1D(N,rL,h,cl)
%
% [f,x] = rsgeng1D(N,rL,h,cl)
%
% generates a 1-dimensional random rough surface f(x) with N surface points.
% The surface has a Gaussian height distribution function and a Gaussian
% autocovariance function, where rL is the length of the surface, h is the
% RMS height and cl is the correlation length.
%
% Input: N - number of surface points
% rL - length of surface
% h - rms height
% cl - correlation length
%
% Output: f - surface heights
% x - surface points
%
% Last updated: 2010-07-26 (David Bergström).
%
format long;
x = linspace(-rL/2,rL/2,N);
Z = h.*randn(1,N); % uncorrelated Gaussian random rough surface distribution
% with mean 0 and standard deviation h
% Gaussian filter
F = exp(-x.^2/(cl^2/2));
% correlation of surface using convolution (faltung), inverse
% Fourier transform and normalizing prefactors
f = sqrt(2/sqrt(pi))*sqrt(rL/N/cl)*ifft(fft(Z).*fft(F));