Есть ли способ конвертировать кватернион в углы?

Question

У меня есть (мировая) матрица, и она применяет перевод, вращение и масштабирование в трехмерный объект. Он создан с функцией XMMatrixTransformation (DirectXMath) и параметр RotationQuaternion сделан вызовом XMQuaternionRotationRollPitchYaw, Затем он сохраняется в файле вместе с другими данными.

Затем мне нужно восстановить значения, чтобы я мог использовать эту функцию для разложения на каждый компонент:

XMMatrixDecompose(&Scale, &RotationQ, &Translation, Matrix);

Масштаб и перевод - векторы, а вращение - кватернион. Если матрица поворачивает объект по одной оси, я мог бы использовать это для преобразования кватерниона обратно в углы:

XMQuaternionToAxisAngle(&Axis, &Angle, RotationQ);

Работает нормально. Но когда он вращается в двух или более осях, как я могу сделать то же самое? Есть способ сделать это?

PS: Мне все равно, если выходные углы не совпадают с входными. Они просто должны быть эквивалентны.

PS2: Хорошо, поэтому я перешел по ссылке Джина (я уже посмотрел там, но не нашел то, что мне было нужно в этот раз). Я сделал этот код на основе этого уравнения, которое я нашел в Википедии: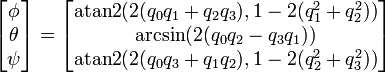

float Roll = atan2(2.0*(F.x*F.y + F.z*F.w), 1 - 2 * (F.y*F.y + F.z*F.z));
float Pitch = asin(2.0*(F.x*F.z - F.w*F.y));
float Yaw = atan2(2.0*(F.x*F.w + F.y*F.z), 1 - 2 * (F.y*F.y + F.z*F.z));

На выходе у меня разные углы. Выход, кажется, эквивалентен для (90°, 0°, 90°), но не для (45°, 45°, 45°),

Answer 1

У вас есть два варианта.

Вы все еще можете использовать функцию XMQuaternionToAxisAngle(), и она будет использовать ось, отличную от кардинальных осей. Любое вращение может быть представлено как один угол, вращающийся вокруг данной оси.

С другой стороны, если вам действительно нужно получить его как углы Эйлера, нет хорошей функции сделать это для вас. Формулы легко доступны, хотя. Из Википедии:

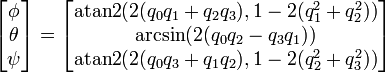
Согласно определению Википедии, phi - это угол вокруг глобальной оси Z, theta - угол вокруг "нормальной оси" N (оси, проходящей через локальное начало и ортогональной плоскости глобальной оси Z и конечной локальной оси Z). ось - да, это немного странно), а пси - это угол вокруг локальной (то есть повернутой) оси Z.

Если бы я был лучшим математиком, я мог бы помочь вам перевести это просто в глобальное вращение X, Y, Z, но, к сожалению, это выходит за рамки моих возможностей.

Просто знайте, что нет строгой корреляции 1-1 между кватернионами и углами Эйлера; Блокировка карданного подвеса означает, что существуют определенные углы, например, с одним и тем же углом Эйлера. Подумайте, действительно ли вам нужны углы Эйлера - в большинстве случаев вращение по оси будет работать точно так же, без значительных проблем с углами Эйлера.