Почему InterpolatedUnivariateSpline возвращает значения нан

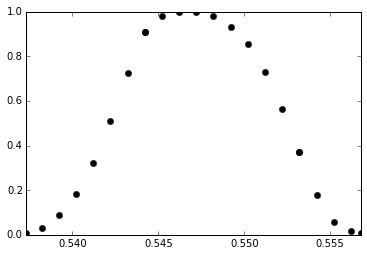
У меня есть некоторые данные, y против x, который я хотел бы интерполировать с более высоким разрешением xx используя кубический сплайн.

Вот мой набор данных:

import numpy as np
print np.version.version
import scipy
print scipy.version.version

1.9.2
0.15.1

x = np.array([0.5372973, 0.5382103, 0.5392305, 0.5402197, 0.5412042, 0.54221, 0.543209,
              0.5442277, 0.5442277, 0.5452125, 0.546217, 0.5472153, 0.5482086,
              0.5492241, 0.5502117, 0.5512249, 0.5522136, 0.5532056, 0.5532056,
              0.5542281, 0.5552039, 0.5562125, 0.5567836])
y = np.array([0.01, 0.03108, 0.08981, 0.18362, 0.32167, 0.50941, 0.72415, 0.90698,
              0.9071, 0.97955, 0.99802, 1., 0.97863, 0.9323, 0.85344, 0.72936,
              0.56413, 0.36997, 0.36957, 0.17623, 0.05922, 0.0163, 0.01, ])

xx = np.array([0.5372981, 0.5374106, 0.5375231, 0.5376356, 0.5377481, 0.5378606,
               0.5379731, 0.5380856, 0.5381981, 0.5383106, 0.5384231, 0.5385356,
               0.5386481, 0.5387606, 0.5388731, 0.5389856, 0.5390981, 0.5392106,
               0.5393231, 0.5394356, 0.5395481, 0.5396606, 0.5397731, 0.5398856,
               0.5399981, 0.5401106, 0.5402231, 0.5403356, 0.5404481, 0.5405606,
               0.5406731, 0.5407856, 0.5408981, 0.5410106, 0.5411231, 0.5412356,
               0.5413481, 0.5414606, 0.5415731, 0.5416856, 0.5417981, 0.5419106,
               0.5420231, 0.5421356, 0.5422481, 0.5423606, 0.5424731, 0.5425856,
               0.5426981, 0.5428106, 0.5429231, 0.5430356, 0.5431481, 0.5432606,
               0.5433731, 0.5434856, 0.5435981, 0.5437106, 0.5438231, 0.5439356,
               0.5440481, 0.5441606, 0.5442731, 0.5443856, 0.5444981, 0.5446106,
               0.5447231, 0.5448356, 0.5449481, 0.5450606, 0.5451731, 0.5452856,
               0.5453981, 0.5455106, 0.5456231, 0.5457356, 0.5458481, 0.5459606,
               0.5460731, 0.5461856, 0.5462981, 0.5464106, 0.5465231, 0.5466356,
               0.5467481, 0.5468606, 0.5469731, 0.5470856, 0.5471981, 0.5473106,
               0.5474231, 0.5475356, 0.5476481, 0.5477606, 0.5478731, 0.5479856,
               0.5480981, 0.5482106, 0.5483231, 0.5484356, 0.5485481, 0.5486606,
               0.5487731, 0.5488856, 0.5489981, 0.5491106, 0.5492231, 0.5493356,
               0.5494481, 0.5495606, 0.5496731, 0.5497856, 0.5498981, 0.5500106,
               0.5501231, 0.5502356, 0.5503481, 0.5504606, 0.5505731, 0.5506856,
               0.5507981, 0.5509106, 0.5510231, 0.5511356, 0.5512481, 0.5513606,
               0.5514731, 0.5515856, 0.5516981, 0.5518106, 0.5519231, 0.5520356,
               0.5521481, 0.5522606, 0.5523731, 0.5524856, 0.5525981, 0.5527106,
               0.5528231, 0.5529356, 0.5530481, 0.5531606, 0.5532731, 0.5533856,
               0.5534981, 0.5536106, 0.5537231, 0.5538356, 0.5539481, 0.5540606,
               0.5541731, 0.5542856, 0.5543981, 0.5545106, 0.5546231, 0.5547356,
               0.5548481, 0.5549606, 0.5550731, 0.5551856, 0.5552981, 0.5554106,
               0.5555231, 0.5556356, 0.5557481, 0.5558606, 0.5559731, 0.5560856,
               0.5561981, 0.5563106, 0.5564231, 0.5565356, 0.5566481, 0.5567606])

Я пытаюсь соответствовать, используя scipy InterpolatedUnivariateSpline метод, интерполированный сплайном 3-го порядка k=3и экстраполируется как нули ext='zeros':

import scipy.interpolate as interp
yspline = interp.InterpolatedUnivariateSpline(x,y, k=3, ext='zeros')
yvals = yspline(xx)

import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y, 'ko', label='Values')
ax.plot(xx, yvals, 'b-.', lw=2, label='Spline')
plt.xlim([min(x), max(x)])

Y против X

Однако, как вы можете видеть на этом изображении, мой сплайн возвращается NaN значения:(Есть ли причина? Я почти уверен, что все мои значения x увеличиваются, поэтому я озадачен тем, почему это происходит. У меня есть много других наборов данных, которые я подгоняю, используя этот метод, и он не работает только на этом конкретном наборе данных.

Любая помощь с благодарностью. Спасибо за чтение.

РЕДАКТИРОВАТЬ!

Решение состояло в том, что у меня есть дубликат x значения, отличающиеся y ценности!

Источник

2 ответа

Решение

Для этой интерполяции лучше использовать scipy.interpolate.interp1d с аргументом kind='cubic' (см. связанный вопрос SO)

Я еще не нашел случай использования, где InterpolatedUnivariateSpline может быть использован на практике (или, может быть, я просто не понимаю его цель). С твоим кодом я получаю, 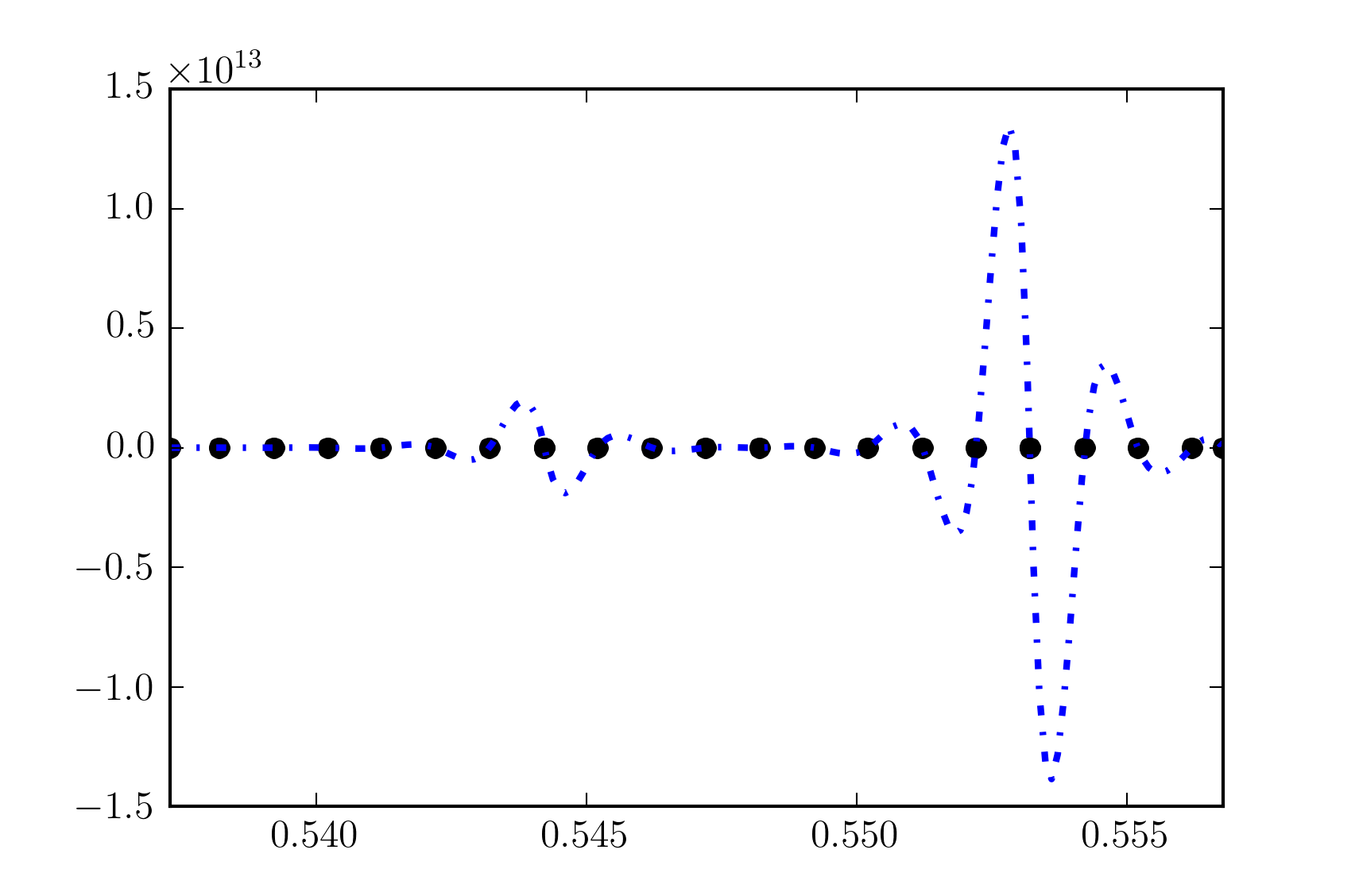сплайн-интерполяция

Таким образом, интерполяция работает, но показывает чрезвычайно сильные колебания, что делает ее непригодной для использования, что, как правило, является результатом, который я получил с помощью этого метода интерполяции в прошлом. Со сплайном более низкого порядка (например, k=1) это работает лучше, но тогда вы теряете преимущество кубической интерполяции.

Источник

Я также столкнулся с проблемой InterpolatedUnivariateSpline возвращая значения NaN. Но в моем случае причина не в том, чтобы дубликаты в x массив, но потому что значения в x уменьшались, когда документы утверждали, что значения "должны увеличиваться".
Итак, в таком случае вместо оригинального x а также y нужно поставить их в обратном порядке: x[::-1] а также y[::-1],

Источник
Другие вопросы по тегам