Python interp1d против UnivariateSpline

Question

Я пытаюсь перенести некоторый код MatLab на Scipy, и я попробовал две разные функции из scipy.interpolate, interp1d и UnivariateSpline. Результаты interp1d соответствуют функции Interp1d MatLab, но числа UnivariateSpline получаются разными, а в некоторых случаях очень разными.

f = interp1d(row1,row2,kind='cubic',bounds_error=False,fill_value=numpy.max(row2))
return  f(interp)

f = UnivariateSpline(row1,row2,k=3,s=0)
return f(interp)

Может ли кто-нибудь предложить какое-либо понимание? Мои значения x не распределены одинаково, хотя я не уверен, почему это так важно.

Answer 1

Я просто столкнулся с той же проблемой.

Короткий ответ

Вместо этого используйте InterpolatedUnivariateSpline:

f = InterpolatedUnivariateSpline(row1, row2)
return f(interp)

Длинный ответ

UnivariateSpline является "одномерным сглаживающим сплайном, подходящим для данного набора точек данных", тогда как InterpolatedUnivariateSpline является "одномерным интерполирующим сплайном для данного набора точек данных". Первый сглаживает данные, тогда как второй является более традиционным методом интерполяции и воспроизводит результаты, ожидаемые от interp1d. На рисунке ниже показано различие.

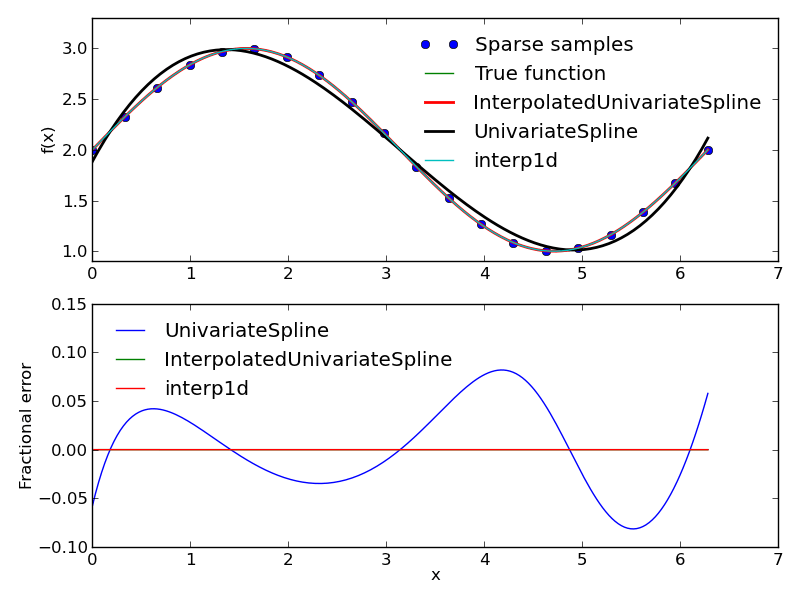
Код для воспроизведения рисунка показан ниже.

import scipy.interpolate as ip

#Define independent variable
sparse = linspace(0, 2 * pi, num = 20)
dense = linspace(0, 2 * pi, num = 200)

#Define function and calculate dependent variable
f = lambda x: sin(x) + 2
fsparse = f(sparse)
fdense = f(dense)

ax = subplot(2, 1, 1)

#Plot the sparse samples and the true function
plot(sparse, fsparse, label = 'Sparse samples', linestyle = 'None', marker = 'o')
plot(dense, fdense, label = 'True function')

#Plot the different interpolation results
interpolate = ip.InterpolatedUnivariateSpline(sparse, fsparse)
plot(dense, interpolate(dense), label = 'InterpolatedUnivariateSpline', linewidth = 2)

smoothing = ip.UnivariateSpline(sparse, fsparse)
plot(dense, smoothing(dense), label = 'UnivariateSpline', color = 'k', linewidth = 2)

ip1d = ip.interp1d(sparse, fsparse, kind = 'cubic')
plot(dense, ip1d(dense), label = 'interp1d')

ylim(.9, 3.3)

legend(loc = 'upper right', frameon = False)

ylabel('f(x)')

#Plot the fractional error
subplot(2, 1, 2, sharex = ax)

plot(dense, smoothing(dense) / fdense - 1, label = 'UnivariateSpline')
plot(dense, interpolate(dense) / fdense - 1, label = 'InterpolatedUnivariateSpline')
plot(dense, ip1d(dense) / fdense - 1, label = 'interp1d')

ylabel('Fractional error')
xlabel('x')
ylim(-.1,.15)

legend(loc = 'upper left', frameon = False)

tight_layout()

Answer 2

Причина, по которой результаты различаются (но оба, вероятно, верны), заключается в том, что процедуры интерполяции, используемые UnivariateSpline а также interp1d разные.

• interp1d строит гладкий B-сплайн, используя x-точки, которые вы дали ему в виде узлов

• UnivariateSpline основан на FITPACK, который также создает гладкий B-сплайн. Тем не менее, FITPACK пытается выбрать новые узлы для сплайна, чтобы лучше соответствовать данным (возможно, чтобы минимизировать chi^2 плюс некоторый штраф за кривизну или что-то подобное). Вы можете узнать, какие узлы использовались через g.get_knots(),

Поэтому причина, по которой вы получаете разные результаты, заключается в том, что алгоритм интерполяции отличается. Если вы хотите B-сплайны с узлами в точках данных, используйте interp1d или же splmake, Если вы хотите, чтобы FITPACK делал, используйте UnivariateSpline, В пределе плотных данных оба метода дают одинаковые результаты, но когда данных мало, вы можете получить разные результаты.

(Откуда я все это знаю: я прочитал код:-)

Answer 3

Работает для меня,

from scipy import allclose, linspace
from scipy.interpolate import interp1d, UnivariateSpline

from numpy.random import normal

from pylab import plot, show

n = 2**5

x = linspace(0,3,n)
y = (2*x**2 + 3*x + 1) + normal(0.0,2.0,n)

i = interp1d(x,y,kind=3)
u = UnivariateSpline(x,y,k=3,s=0)

m = 2**4

t = linspace(1,2,m)

plot(x,y,'r,')
plot(t,i(t),'b')
plot(t,u(t),'g')

print allclose(i(t),u(t)) # evaluates to True

show()

Это дает мне,

Answer 4

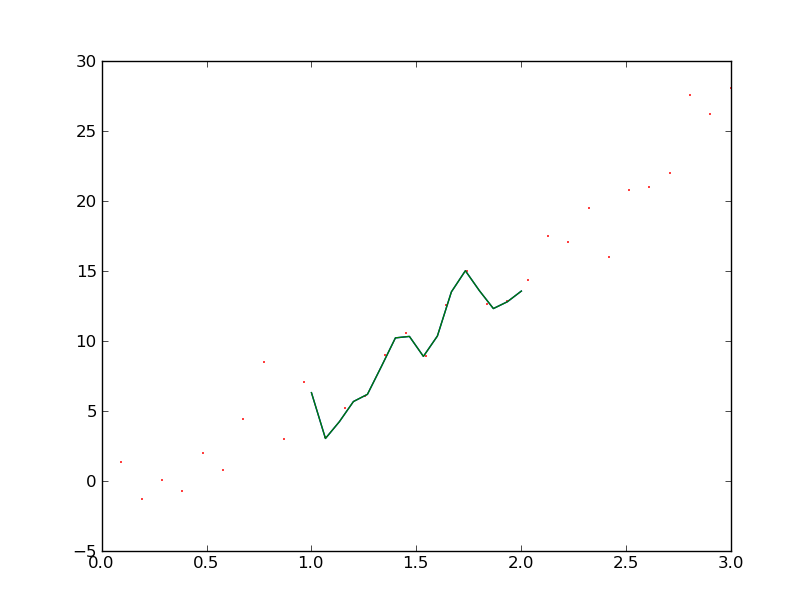
UnivariateSpline: более поздняя оболочка подпрограмм FITPACK.

это может объяснить немного другие значения? (Я также испытал, что UnivariateSpline намного быстрее, чем interp1d.)