Точный субпиксельный алгоритм рисования линий (алгоритм растеризации)

Question

Мне нужен алгоритм, который может быть (немного) медленнее, чем алгоритм рисования линий Брезенхэма, но должен быть намного более точным. Под "точным" я подразумеваю: каждый потроганный пиксель должен быть напечатан. Не больше, но и не меньше! Это означает, что использование более толстой линии или подобного не подходит, так как будет задействовано слишком много пикселей. Также мне не нужна графическая структура или что-то подобное, как это было задано ранее, мне нужен алгоритм! Приложение на самом деле не в "графике", а в географической области, где пиксели являются "плитками".

Основная проблема для меня заключается в том, что мне нужна субпиксельная точность, что означает, что строка может начинаться с 0,75/0,33, а не только с 0/0, как это имеет место для целочисленных значений. Я пытался создать рабочее решение за последние несколько часов, но не могу заставить его работать - слишком много крайних случаев.

Сначала я подумал, что сглаженная версия, такая как алгоритм Wu, должна сделать это, но она печатает слишком много пикселей (особенно для начальной и конечной точек), и в некоторых случаях она по-прежнему пропускает некоторые пиксели, например, для очень коротких линий.

Затем я попытался заставить Брезенхема работать там, где я заменил второе "если" на "еще, если", как указано здесь, и оно ближе, но все еще не там. Затем я попытался перевести Bresenham с целочисленной точности на плавающую, что привело к бесконечному циклу (поскольку значения x,y перепрыгивали через условие завершения if (y1 == y2 && x1 == x2)).

Я мог бы использовать наивное решение для рисования линий, но который delta я должен использовать? Например, если я использую 0.1, я все еще буду пропускать некоторые пиксели, а при использовании меньших значений это, вероятно, займет слишком много времени (и все еще будет пропускать пиксели).

Рабочее решение в C/Java/... будет приветствоваться. По крайней мере, он должен работать для октанта 1, но полноценное решение будет еще лучше.

Обновление: мне пришла в голову следующая идея: использовать растеризацию наивной линии, и вы можете рассчитать 4 пиксельных кандидата на каждую точку. Затем проверьте эти 4 пикселя, действительно ли линия пересекает их. Но я не уверен, что пересечение линии / коробки может быть достаточно быстрым.

Answer 1

Если вам нужен только постоянный цвет (не интерполированный по используемой площади пикселя), используйте DDA:

void line_DDA_subpixel(int x0,int y0,int x1,int y1,int col) // DDA subpixel -> thick
    {
    int kx,ky,c,i,xx,yy,dx,dy;
    x1-=x0; kx=0; if (x1>0) kx=+1; if (x1<0) { kx=-1; x1=-x1; } x1++;
    y1-=y0; ky=0; if (y1>0) ky=+1; if (y1<0) { ky=-1; y1=-y1; } y1++;
    if (x1>=y1)
     for (c=x1,i=0;i<x1;i++,x0+=kx)
        {
        pnt(x0,y0,col); // this is normal pixel the two below are subpixels 
        c-=y1; if (c<=0) { if (i!=x1-1) pnt(x0+kx,y0,col); c+=x1; y0+=ky; if (i!=x1-1) pnt(x0,y0,col); }
        }
    else
     for (c=y1,i=0;i<y1;i++,y0+=ky)
        {
        pnt(x0,y0,col); // this is normal pixel the two below are subpixels 
        c-=x1; if (c<=0) { if (i!=y1-1) pnt(x0,y0+ky,col); c+=y1; x0+=kx; if (i!=y1-1) pnt(x0,y0,col); }
        }
    }

где:

void pnt(int x,int y,int col);

это обычная процедура растеризации пикселя (x,y) с цветом col Источник в C++

Я думаю, что это прямолинейно, но в любом случае

DDA использует параметрическое линейное уравнение y=k*x+q или же x=ky+q зависит от разницы (если больше x или же y разница так что дыр нет). k является dy/dx или же dx/dy и все деление сводится к вычитанию + сложению внутри цикла (последняя строка каждого цикла). Это может быть легко изменено на любое количество измерений (я обычно использую 7D или больше с этим). На современных машинах скорость иногда лучше, чем у Bresenham (зависит от платформы и использования).

Вот так это выглядит по сравнению с простым DDA

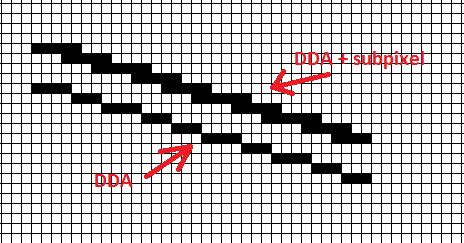
[edit2] двойные координаты // первоначально [edit1]

ОК, вот новый код:

void line_DDA_subpixel1(double x0,double y0,double x1,double y1,int col)    // DDA subpixel -> thick
    {
    int i,n,x,y,xx,yy;
    // prepare data n-pixels,x1,y1 is line dx,dy step per pixel
    x1-=x0; i=ceil(fabs(x1));
    y1-=y0; n=ceil(fabs(y1));
    if (n<i) n=i; if (!n) n=1;
    x1/=double(n);
    y1/=double(n); n++;
    // rasterize DDA line
    for (xx=x0,yy=y0,i=0;i<=n;i++,x0+=x1,y0+=y1)
        {
        // direct pixel
        pnt(x,y,col);
        // subpixels on change in both axises
        x=x0; y=y0;
        if ((i<n)&&(x!=xx)&&(y!=yy)) { pnt(xx,y,col); pnt(x,yy,col); }
        xx=x; yy=y;
        }
    }

И вот как это выглядит:

Угол должен быть в double точность сейчас, но pnt(x,y,col) все еще на целых числах!!!

[edit3] пересечение сетки пикселей

void DDAf_line_subpixel(float x0,float y0,float x1,float y1,int col)    // DDA subpixel -> thick
    {
    int i,n; float a,a0,a1,aa,b,d;
    // end-points
    pnt(x0,y0,col);
    pnt(x1,y1,col);
    // x-axis pixel cross
    a0=1; a1=0; n=0;
    if (x0<x1) { a0=ceil(x0); a1=floor(x1); d=(y1-y0)/(x1-x0); a=a0; b=y0+(a0-x0)*d; n=fabs(a1-a0); } else
    if (x0>x1) { a0=ceil(x1); a1=floor(x0); d=(y1-y0)/(x1-x0); a=a0; b=y1+(a0-x1)*d; n=fabs(a1-a0); }
    if (a0<=a1) for (aa=a,i=0;i<=n;i++,aa=a,a++,b+=d) { pnt(aa,b,col); pnt( a,b,col); }
    // y-axis pixel cross
    a0=1; a1=0; n=0;
    if (y0<y1) { a0=ceil(y0); a1=floor(y1); d=(x1-x0)/(y1-y0); a=a0; b=x0+(a0-y0)*d; n=fabs(a1-a0); } else
    if (y0>y1) { a0=ceil(y1); a1=floor(y0); d=(x1-x0)/(y1-y0); a=a0; b=x1+(a0-y1)*d; n=fabs(a1-a0); }
    if (a0<=a1) for (aa=a,i=0;i<=n;i++,aa=a,a++,b+=d) { pnt(b,aa,col); pnt(b, a,col); }
    }

Наконец-то было время для этого, поэтому я немного подправил DDA, но id привел ко многим ifТак что я немного изменил растеризацию. Теперь все пересечения сетки пикселей (пересечения) вычисляются, а затем для каждого добавляется правый подпиксель. Вот как это выглядит (без неправильных подпикселей):

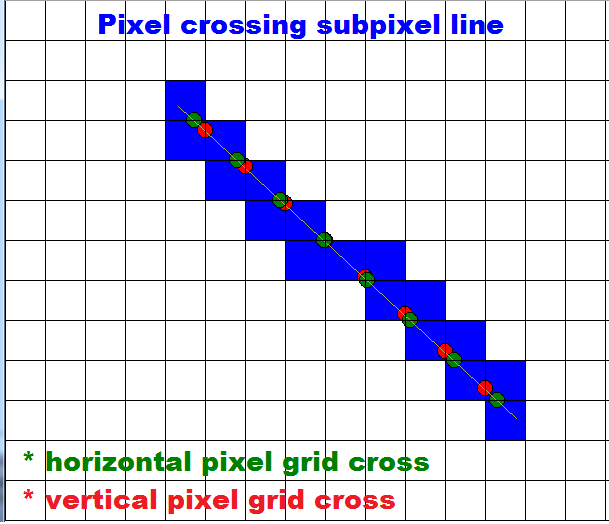
Для каждого x или же y линии сетки - это первая точка пересечения (a,b) а также step находится в одной оси 1 пиксель и в секунду остальные в соответствии с dy/dx или же dx/dy, После этого цикл for заполняет субпиксели...

Answer 2

Если ваша линия тонкая, а пиксели прямоугольные (квадратные):

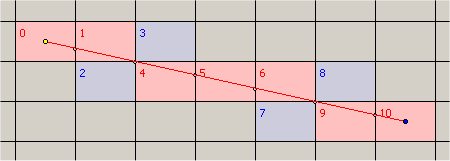
затем рассмотрите возможность использования алгоритмов обхода воксельной сетки, например, см. статью " Быстрый алгоритм обхода вокселей ... " Ву и Аманатида.

Практическая реализация (в разделе обхода сетки)

Ответ на комментарий:
Правильная инициализация для координатных переменных (то же самое для Y)

  DX = X2 - X1
  tDeltaX = GridCellWidth / DX
  tMaxX = tDeltaX * (1.0 - Frac(X1 / GridCellWidth)) 
  //Frac if fractional part of float, for example, Frac(1.3) = 0.3

пример в моем ответе здесь