Как нарисовать перспективную сетку в 2D
У меня есть приложение, которое определяет прямоугольник реального мира поверх изображения / фотографии, конечно, в 2D это может быть не прямоугольник, потому что вы смотрите на него под углом.
Проблема, скажем, в том, что на прямоугольнике должны быть нарисованы линии сетки, например, если это 3x5, поэтому мне нужно нарисовать 2 линии от стороны 1 до стороны 3 и 4 линии от стороны 2 до стороны 4.
На данный момент я разбиваю каждую линию на равноотстоящие части, чтобы получить начальную и конечную точку всех линий сетки. Однако чем больше угол наклона прямоугольника, тем более "неправильными" становятся эти линии, так как горизонтальные линии дальше от вас должны быть ближе друг к другу.
Кто-нибудь знает название алгоритма, который я должен искать?
Да, я знаю, что вы можете сделать это в 3D, однако я ограничен 2D для этого конкретного приложения.
11 ответов
Вот решение: http://freespace.virgin.net/hugo.elias/graphics/x_persp.htm
Основная идея заключается в том, что вы можете найти перспективный правильный "центр" вашего прямоугольника, соединяя углы по диагонали. Пересечение двух результирующих линий - это ваш правильный центр перспективы. Оттуда вы подразделяете свой прямоугольник на четыре меньших прямоугольника и повторяете процесс. Количество раз зависит от того, насколько точно вы этого хотите. Вы можете разделить чуть ниже размера пикселя для эффективной идеальной перспективы.
Затем в ваших под прямоугольниках вы просто применяете свои стандартные нескорректированные "текстурированные" треугольники или прямоугольники или что-то еще.
Вы можете выполнить этот алгоритм, не вдаваясь в сложные проблемы построения "настоящего" трехмерного мира. Это также хорошо, если у вас есть смоделированный реальный трехмерный мир, но ваши текстовые треугольники не исправлены в перспективе аппаратно, или вам нужен эффективный способ получения правильных перспективных плоскостей без хитрости рендеринга за пиксель.
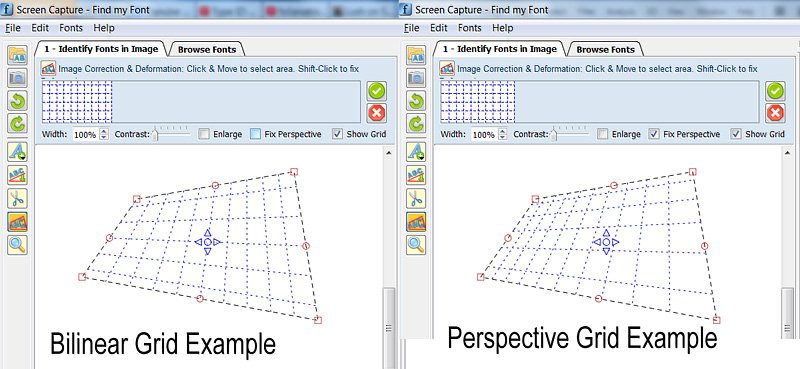 Изображение: пример билинейного и перспективного преобразования (примечание: высота верхней и нижней горизонтальных линий сетки фактически равна половине высоты остальных линий на обоих чертежах)
Изображение: пример билинейного и перспективного преобразования (примечание: высота верхней и нижней горизонтальных линий сетки фактически равна половине высоты остальных линий на обоих чертежах)
========================================
Я знаю, что это старый вопрос, но у меня есть общее решение, поэтому я решил опубликовать его, но оно будет полезно для будущих читателей. Код ниже может нарисовать произвольную перспективную сетку без необходимости повторных вычислений.
На самом деле я начинаю с аналогичной проблемы: нарисовать 2D перспективную сетку, а затем трансформировать изображение подчеркивания, чтобы восстановить перспективу.
Я начал читать здесь: http://www.imagemagick.org/Usage/distorts/
и затем здесь (Библиотека Лептоники): http://www.leptonica.com/affine.html
где я нашел это:
Когда вы смотрите на объект в плоскости с произвольного направления на конечном расстоянии, вы получаете дополнительное искажение "краеугольного камня" на изображении. Это проективное преобразование, которое сохраняет прямые линии прямыми, но не сохраняет углы между линиями. Эта деформация не может быть описана линейным аффинным преобразованием, и фактически отличается знаменателем от x- и y-зависимых членов.
Преобразование не является линейным, как многие люди уже указали в этой теме. Это включает решение линейной системы из 8 уравнений (один раз) для вычисления 8 требуемых коэффициентов, а затем вы можете использовать их для преобразования столько точек, сколько вы хотите.
Чтобы не включать в свой проект всю библиотеку Leptonica, я взял из нее несколько фрагментов кода, удалил все специальные типы данных и макросы Leptonica, исправил некоторые утечки памяти и преобразовал их в класс C++ (в основном из соображений инкапсуляции), который делает только одно: он отображает координату (Qt) QPointF float (x,y) в соответствующую координату перспективы.
Если вы хотите адаптировать код к другой библиотеке C++, единственное, что нужно переопределить / заменить, - это класс координат QPointF.
Я надеюсь, что некоторые будущие читатели найдут это полезным. Код ниже разделен на 3 части:
A. Пример того, как использовать класс genImageProjective C++ для рисования 2D перспективной сетки
B. genImageProjective.h файл
C. genImageProjective.cpp файл
//============================================================
// C++ Code Example on how to use the
// genImageProjective class to draw a perspective 2D Grid
//============================================================
#include "genImageProjective.h"
// Input: 4 Perspective-Tranformed points:
// perspPoints[0] = top-left
// perspPoints[1] = top-right
// perspPoints[2] = bottom-right
// perspPoints[3] = bottom-left
void drawGrid(QPointF *perspPoints)
{
(...)
// Setup a non-transformed area rectangle
// I use a simple square rectangle here because in this case we are not interested in the source-rectangle,
// (we want to just draw a grid on the perspPoints[] area)
// but you can use any arbitrary rectangle to perform a real mapping to the perspPoints[] area
QPointF topLeft = QPointF(0,0);
QPointF topRight = QPointF(1000,0);
QPointF bottomRight = QPointF(1000,1000);
QPointF bottomLeft = QPointF(0,1000);
float width = topRight.x() - topLeft.x();
float height = bottomLeft.y() - topLeft.y();
// Setup Projective trasform object
genImageProjective imageProjective;
imageProjective.sourceArea[0] = topLeft;
imageProjective.sourceArea[1] = topRight;
imageProjective.sourceArea[2] = bottomRight;
imageProjective.sourceArea[3] = bottomLeft;
imageProjective.destArea[0] = perspPoints[0];
imageProjective.destArea[1] = perspPoints[1];
imageProjective.destArea[2] = perspPoints[2];
imageProjective.destArea[3] = perspPoints[3];
// Compute projective transform coefficients
if (imageProjective.computeCoeefficients() != 0)
return; // This can actually fail if any 3 points of Source or Dest are colinear
// Initialize Grid parameters (without transform)
float gridFirstLine = 0.1f; // The normalized position of first Grid Line (0.0 to 1.0)
float gridStep = 0.1f; // The normalized Grd size (=distance between grid lines: 0.0 to 1.0)
// Draw Horizonal Grid lines
QPointF lineStart, lineEnd, tempPnt;
for (float pos = gridFirstLine; pos <= 1.0f; pos += gridStep)
{
// Compute Grid Line Start
tempPnt = QPointF(topLeft.x(), topLeft.y() + pos*width);
imageProjective.mapSourceToDestPoint(tempPnt, lineStart);
// Compute Grid Line End
tempPnt = QPointF(topRight.x(), topLeft.y() + pos*width);
imageProjective.mapSourceToDestPoint(tempPnt, lineEnd);
// Draw Horizontal Line (use your prefered method to draw the line)
(...)
}
// Draw Vertical Grid lines
for (float pos = gridFirstLine; pos <= 1.0f; pos += gridStep)
{
// Compute Grid Line Start
tempPnt = QPointF(topLeft.x() + pos*height, topLeft.y());
imageProjective.mapSourceToDestPoint(tempPnt, lineStart);
// Compute Grid Line End
tempPnt = QPointF(topLeft.x() + pos*height, bottomLeft.y());
imageProjective.mapSourceToDestPoint(tempPnt, lineEnd);
// Draw Vertical Line (use your prefered method to draw the line)
(...)
}
(...)
}
==========================================
//========================================
//C++ Header File: genImageProjective.h
//========================================
#ifndef GENIMAGE_H
#define GENIMAGE_H
#include <QPointF>
// Class to transform an Image Point using Perspective transformation
class genImageProjective
{
public:
genImageProjective();
int computeCoeefficients(void);
int mapSourceToDestPoint(QPointF& sourcePoint, QPointF& destPoint);
public:
QPointF sourceArea[4]; // Source Image area limits (Rectangular)
QPointF destArea[4]; // Destination Image area limits (Perspectivelly Transformed)
private:
static int gaussjordan(float **a, float *b, int n);
bool coefficientsComputed;
float vc[8]; // Vector of Transform Coefficients
};
#endif // GENIMAGE_H
//========================================
//========================================
//C++ CPP File: genImageProjective.cpp
//========================================
#include <math.h>
#include "genImageProjective.h"
// ----------------------------------------------------
// class genImageProjective
// ----------------------------------------------------
genImageProjective::genImageProjective()
{
sourceArea[0] = sourceArea[1] = sourceArea[2] = sourceArea[3] = QPointF(0,0);
destArea[0] = destArea[1] = destArea[2] = destArea[3] = QPointF(0,0);
coefficientsComputed = false;
}
// --------------------------------------------------------------
// Compute projective transform coeeeficients
// RetValue: 0: Success, !=0: Error
/*-------------------------------------------------------------*
* Projective coordinate transformation *
*-------------------------------------------------------------*/
/*!
* computeCoeefficients()
*
* Input: this->sourceArea[4]: (source 4 points; unprimed)
* this->destArea[4]: (transformed 4 points; primed)
* this->vc (computed vector of transform coefficients)
* Return: 0 if OK; <0 on error
*
* We have a set of 8 equations, describing the projective
* transformation that takes 4 points (sourceArea) into 4 other
* points (destArea). These equations are:
*
* x1' = (c[0]*x1 + c[1]*y1 + c[2]) / (c[6]*x1 + c[7]*y1 + 1)
* y1' = (c[3]*x1 + c[4]*y1 + c[5]) / (c[6]*x1 + c[7]*y1 + 1)
* x2' = (c[0]*x2 + c[1]*y2 + c[2]) / (c[6]*x2 + c[7]*y2 + 1)
* y2' = (c[3]*x2 + c[4]*y2 + c[5]) / (c[6]*x2 + c[7]*y2 + 1)
* x3' = (c[0]*x3 + c[1]*y3 + c[2]) / (c[6]*x3 + c[7]*y3 + 1)
* y3' = (c[3]*x3 + c[4]*y3 + c[5]) / (c[6]*x3 + c[7]*y3 + 1)
* x4' = (c[0]*x4 + c[1]*y4 + c[2]) / (c[6]*x4 + c[7]*y4 + 1)
* y4' = (c[3]*x4 + c[4]*y4 + c[5]) / (c[6]*x4 + c[7]*y4 + 1)
*
* Multiplying both sides of each eqn by the denominator, we get
*
* AC = B
*
* where B and C are column vectors
*
* B = [ x1' y1' x2' y2' x3' y3' x4' y4' ]
* C = [ c[0] c[1] c[2] c[3] c[4] c[5] c[6] c[7] ]
*
* and A is the 8x8 matrix
*
* x1 y1 1 0 0 0 -x1*x1' -y1*x1'
* 0 0 0 x1 y1 1 -x1*y1' -y1*y1'
* x2 y2 1 0 0 0 -x2*x2' -y2*x2'
* 0 0 0 x2 y2 1 -x2*y2' -y2*y2'
* x3 y3 1 0 0 0 -x3*x3' -y3*x3'
* 0 0 0 x3 y3 1 -x3*y3' -y3*y3'
* x4 y4 1 0 0 0 -x4*x4' -y4*x4'
* 0 0 0 x4 y4 1 -x4*y4' -y4*y4'
*
* These eight equations are solved here for the coefficients C.
*
* These eight coefficients can then be used to find the mapping
* (x,y) --> (x',y'):
*
* x' = (c[0]x + c[1]y + c[2]) / (c[6]x + c[7]y + 1)
* y' = (c[3]x + c[4]y + c[5]) / (c[6]x + c[7]y + 1)
*
*/
int genImageProjective::computeCoeefficients(void)
{
int retValue = 0;
int i;
float *a[8]; /* 8x8 matrix A */
float *b = this->vc; /* rhs vector of primed coords X'; coeffs returned in vc[] */
b[0] = destArea[0].x();
b[1] = destArea[0].y();
b[2] = destArea[1].x();
b[3] = destArea[1].y();
b[4] = destArea[2].x();
b[5] = destArea[2].y();
b[6] = destArea[3].x();
b[7] = destArea[3].y();
for (i = 0; i < 8; i++)
a[i] = NULL;
for (i = 0; i < 8; i++)
{
if ((a[i] = (float *)calloc(8, sizeof(float))) == NULL)
{
retValue = -100; // ERROR_INT("a[i] not made", procName, 1);
goto Terminate;
}
}
a[0][0] = sourceArea[0].x();
a[0][1] = sourceArea[0].y();
a[0][2] = 1.;
a[0][6] = -sourceArea[0].x() * b[0];
a[0][7] = -sourceArea[0].y() * b[0];
a[1][3] = sourceArea[0].x();
a[1][4] = sourceArea[0].y();
a[1][5] = 1;
a[1][6] = -sourceArea[0].x() * b[1];
a[1][7] = -sourceArea[0].y() * b[1];
a[2][0] = sourceArea[1].x();
a[2][1] = sourceArea[1].y();
a[2][2] = 1.;
a[2][6] = -sourceArea[1].x() * b[2];
a[2][7] = -sourceArea[1].y() * b[2];
a[3][3] = sourceArea[1].x();
a[3][4] = sourceArea[1].y();
a[3][5] = 1;
a[3][6] = -sourceArea[1].x() * b[3];
a[3][7] = -sourceArea[1].y() * b[3];
a[4][0] = sourceArea[2].x();
a[4][1] = sourceArea[2].y();
a[4][2] = 1.;
a[4][6] = -sourceArea[2].x() * b[4];
a[4][7] = -sourceArea[2].y() * b[4];
a[5][3] = sourceArea[2].x();
a[5][4] = sourceArea[2].y();
a[5][5] = 1;
a[5][6] = -sourceArea[2].x() * b[5];
a[5][7] = -sourceArea[2].y() * b[5];
a[6][0] = sourceArea[3].x();
a[6][1] = sourceArea[3].y();
a[6][2] = 1.;
a[6][6] = -sourceArea[3].x() * b[6];
a[6][7] = -sourceArea[3].y() * b[6];
a[7][3] = sourceArea[3].x();
a[7][4] = sourceArea[3].y();
a[7][5] = 1;
a[7][6] = -sourceArea[3].x() * b[7];
a[7][7] = -sourceArea[3].y() * b[7];
retValue = gaussjordan(a, b, 8);
Terminate:
// Clean up
for (i = 0; i < 8; i++)
{
if (a[i])
free(a[i]);
}
this->coefficientsComputed = (retValue == 0);
return retValue;
}
/*-------------------------------------------------------------*
* Gauss-jordan linear equation solver *
*-------------------------------------------------------------*/
/*
* gaussjordan()
*
* Input: a (n x n matrix)
* b (rhs column vector)
* n (dimension)
* Return: 0 if ok, 1 on error
*
* Note side effects:
* (1) the matrix a is transformed to its inverse
* (2) the vector b is transformed to the solution X to the
* linear equation AX = B
*
* Adapted from "Numerical Recipes in C, Second Edition", 1992
* pp. 36-41 (gauss-jordan elimination)
*/
#define SWAP(a,b) {temp = (a); (a) = (b); (b) = temp;}
int genImageProjective::gaussjordan(float **a, float *b, int n)
{
int retValue = 0;
int i, icol=0, irow=0, j, k, l, ll;
int *indexc = NULL, *indexr = NULL, *ipiv = NULL;
float big, dum, pivinv, temp;
if (!a)
{
retValue = -1; // ERROR_INT("a not defined", procName, 1);
goto Terminate;
}
if (!b)
{
retValue = -2; // ERROR_INT("b not defined", procName, 1);
goto Terminate;
}
if ((indexc = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -3; // ERROR_INT("indexc not made", procName, 1);
goto Terminate;
}
if ((indexr = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -4; // ERROR_INT("indexr not made", procName, 1);
goto Terminate;
}
if ((ipiv = (int *)calloc(n, sizeof(int))) == NULL)
{
retValue = -5; // ERROR_INT("ipiv not made", procName, 1);
goto Terminate;
}
for (i = 0; i < n; i++)
{
big = 0.0;
for (j = 0; j < n; j++)
{
if (ipiv[j] != 1)
{
for (k = 0; k < n; k++)
{
if (ipiv[k] == 0)
{
if (fabs(a[j][k]) >= big)
{
big = fabs(a[j][k]);
irow = j;
icol = k;
}
}
else if (ipiv[k] > 1)
{
retValue = -6; // ERROR_INT("singular matrix", procName, 1);
goto Terminate;
}
}
}
}
++(ipiv[icol]);
if (irow != icol)
{
for (l = 0; l < n; l++)
SWAP(a[irow][l], a[icol][l]);
SWAP(b[irow], b[icol]);
}
indexr[i] = irow;
indexc[i] = icol;
if (a[icol][icol] == 0.0)
{
retValue = -7; // ERROR_INT("singular matrix", procName, 1);
goto Terminate;
}
pivinv = 1.0 / a[icol][icol];
a[icol][icol] = 1.0;
for (l = 0; l < n; l++)
a[icol][l] *= pivinv;
b[icol] *= pivinv;
for (ll = 0; ll < n; ll++)
{
if (ll != icol)
{
dum = a[ll][icol];
a[ll][icol] = 0.0;
for (l = 0; l < n; l++)
a[ll][l] -= a[icol][l] * dum;
b[ll] -= b[icol] * dum;
}
}
}
for (l = n - 1; l >= 0; l--)
{
if (indexr[l] != indexc[l])
{
for (k = 0; k < n; k++)
SWAP(a[k][indexr[l]], a[k][indexc[l]]);
}
}
Terminate:
if (indexr)
free(indexr);
if (indexc)
free(indexc);
if (ipiv)
free(ipiv);
return retValue;
}
// --------------------------------------------------------------
// Map a source point to destination using projective transform
// --------------------------------------------------------------
// Params:
// sourcePoint: initial point
// destPoint: transformed point
// RetValue: 0: Success, !=0: Error
// --------------------------------------------------------------
// Notes:
// 1. You must call once computeCoeefficients() to compute
// the this->vc[] vector of 8 coefficients, before you call
// mapSourceToDestPoint().
// 2. If there was an error or the 8 coefficients were not computed,
// a -1 is returned and destPoint is just set to sourcePoint value.
// --------------------------------------------------------------
int genImageProjective::mapSourceToDestPoint(QPointF& sourcePoint, QPointF& destPoint)
{
if (coefficientsComputed)
{
float factor = 1.0f / (vc[6] * sourcePoint.x() + vc[7] * sourcePoint.y() + 1.);
destPoint.setX( factor * (vc[0] * sourcePoint.x() + vc[1] * sourcePoint.y() + vc[2]) );
destPoint.setY( factor * (vc[3] * sourcePoint.x() + vc[4] * sourcePoint.y() + vc[5]) );
return 0;
}
else // There was an error while computing coefficients
{
destPoint = sourcePoint; // just copy the source to destination...
return -1; // ...and return an error
}
}
//========================================
Хотя мое гугл-фу не смогло найти какого-либо серьезного математического решения, возможно, этот рисунок, который я нашел, мог бы немного помочь.
http://studiochalkboard.evansville.edu/lp-diminish.html
Я думаю, что на самом деле может быть довольно сложно придумать правильную математику самостоятельно, это, вероятно, какое-то логарифмическое или суммирующее выражение. Надеемся, что рисунок и термины по этой ссылке могут предоставить вам что-то более интересное для поиска.
Используя метод деления Бретона (который связан с методом расширения Монго), вы получите точные произвольные деления степени двух. Чтобы разделить на деления не степени двух, используя эти методы, вам придется разделить на подпиксельные интервалы, которые могут быть вычислительно дорогими.
Тем не менее, я полагаю, что вы можете применить вариант теоремы Хага (который используется в оригами, чтобы разделить сторону на N-ю, если сторона разделена на (N-1) -ую), к подразделам в квадрате перспективы для получения произвольных делений из ближайшая степень 2 без необходимости продолжать деление.
Наиболее элегантным и быстрым решением было бы найти матрицу гомографии, которая отображает координаты прямоугольника на координаты фотографии.
Приличная матричная библиотека не должна быть трудной задачей, если вы знаете свою математику.
Ключевые слова: коллинеация, гомография, прямое линейное преобразование
Однако приведенный выше рекурсивный алгоритм должен работать, но, возможно, если ваши ресурсы ограничены, проективная геометрия - единственный путь.
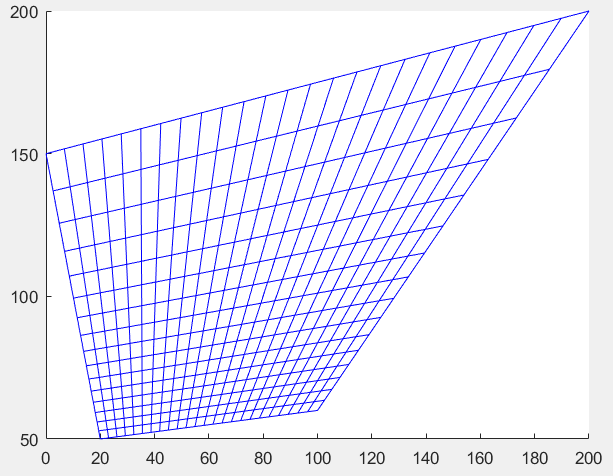
Я думаю, что выбранный ответ - не лучшее доступное решение. Лучшее решение - применить перспективное (проективное) преобразование прямоугольника к простой сетке, как показано в сценарии Matlab и на изображении. Вы можете реализовать этот алгоритм с C++ и OpenCV.
function drawpersgrid
sz = [ 24, 16 ]; % [x y]
srcpt = [ 0 0; sz(1) 0; 0 sz(2); sz(1) sz(2)];
destpt = [ 20 50; 100 60; 0 150; 200 200;];
% make rectangular grid
[X,Y] = meshgrid(0:sz(1),0:sz(2));
% find projective transform matching corner points
tform = maketform('projective',srcpt,destpt);
% apply the projective transform to the grid
[X1,Y1] = tformfwd(tform,X,Y);
hold on;
%% find grid
for i=1:sz(2)
for j=1:sz(1)
x = [ X1(i,j);X1(i,j+1);X1(i+1,j+1);X1(i+1,j);X1(i,j)];
y = [ Y1(i,j);Y1(i,j+1);Y1(i+1,j+1);Y1(i+1,j);Y1(i,j)];
plot(x,y,'b');
end
end
hold off;
Это геометрическое решение я придумал. Я не знаю, есть ли у "алгоритма" имя.
Допустим, вы хотите начать с разделения "прямоугольника" на n частей с вертикальными линиями.
Цель состоит в том, чтобы поместить точки P1..Pn-1 в верхнюю линию, которую мы можем использовать, чтобы провести линии через них к точкам, где левая и правая линии встречаются или параллельны им, когда такая точка не существует.
Если верхняя и нижняя линии параллельны друг другу, просто разместите точки разметки, чтобы разделить верхнюю линию между углами на равном расстоянии.
В противном случае поместите n точек Q1..Qn на левой линии, чтобы они и верхний левый угол были равноудалены, а i
Сделайте этот аналог для горизонтальных линий.
В особом случае, когда вы смотрите перпендикулярно сторонам 1 и 3, вы можете разделить эти стороны на равные части. Затем нарисуйте диагональ и проведите параллели к стороне 1 через каждое пересечение диагонали и разделительных линий, проведенных ранее.
Учитывая вращение вокруг оси y, особенно если поверхности вращения плоские, перспектива создается вертикальными градиентами. Они становятся все ближе в перспективе. Вместо того чтобы использовать диагонали для определения четырех прямоугольников, которые могут работать с заданными степенями двух... задайте два прямоугольника, левый и правый. В конечном итоге они будут выше ширины, если продолжать разделять поверхность на более узкие вертикальные сегменты. Это может приспособить поверхности, которые не являются квадратными. Если вращение вокруг оси х, то необходимы горизонтальные градиенты.
Что вам нужно сделать, это представить его в 3D (мир), а затем спроецировать его в 2D (экран).
Это потребует от вас использования матрицы преобразования 4D, которая делает проекцию на 4D однородной вплоть до однородного вектора 3D, которую затем можно преобразовать в вектор пространства 2D экрана.
Я не смог найти его и в Google, но в хороших книгах по компьютерной графике будут подробности.
Ключевые слова: проекционная матрица, проекционное преобразование, аффинное преобразование, однородный вектор, мировое пространство, пространство экрана, перспективное преобразование, трехмерное преобразование
И, кстати, для объяснения всего этого обычно требуется несколько лекций. Удачи.
Проблема в том, что это переход от 3D к 2D, который вам нужен.
Вот учебник о том, как это делается.