Разработка иерархической версии модели нелинейной кривой роста в Stan
Следующая модель является моделью 1 Preece and Baines (1978, Annals of Human Biology) и используется для описания роста человека.
Мой код Stan для этой модели выглядит следующим образом:
```{stan output.var="test"}
data {
int<lower=1> n;
ordered[n] t; // age
ordered[n] y; // height of human
}
parameters {
positive_ordered[2] h;
real<lower=0, upper=t[n-1]>theta;
positive_ordered[2] s;
real<lower=0>sigma;
}
model {
h[1] ~ uniform(0, y[n]);
h[2] ~ normal(180, 20);
sigma ~ student_t(2, 0, 1);
s[1] ~ normal(5, 5);
s[2] ~ normal(5, 5);
theta ~ normal(10, 5);
y ~ normal(h[2] - (2*(h[2] - h[1]) * inv(exp(s[1]*(t - theta)) + exp(s[2]*(t - theta)))), sigma);
}
```
Теперь я хочу создать иерархическую версию этой модели с параметрами, одинаковыми для мальчиков (например, изменчивость измерения). sigma) или в иерархической версии (например, h_1, рост взрослого).
Что касается параметров sigma а также thetaЯ хочу, чтобы эти приоры были одинаковыми среди мальчиков, sigma ~ student_t(2, 0, 1); а также theta ~ normal(10, 5);,
К сожалению, у меня почти нет опыта в реализации иерархического моделирования, и я изо всех сил пытался создать какие-либо иерархические примеры, помимо простых биномиальных иерархических моделей в байесовских учебниках (см. Главу 12, стр. 358-359 " Статистического переосмысления " Ричарда МакЭлрита). Однако я понимаю теорию иерархического моделирования, изложенную в главе 5 " Анализ байесовских данных " Эндрю Гельмана и в главе 12 " Статистическое переосмысление " Ричарда МакЭлрита.
Я был бы признателен, если бы люди могли потратить время на демонстрацию того, как этот тип иерархической модели будет реализован в Stan. Если не так много вопросов, я был бы очень признателен за любые объяснения, которые вы могли бы дать вместе с кодом, чтобы я мог научиться реализовывать эти типы примеров иерархической модели независимо в будущем.
Пример моих данных выглядит следующим образом:
age boy01 boy02 boy03 boy04 boy05 boy06 boy07 boy08 boy09 boy10 boy11 boy12 boy13 boy14 boy15 boy16 boy17 boy18
1 1 81.3 76.2 76.8 74.1 74.2 76.8 72.4 73.8 75.4 78.8 76.9 81.6 78 76.4 76.4 76.2 75 79.7
2 1.25 84.2 80.4 79.8 78.4 76.3 79.1 76 78.7 81 83.3 79.9 83.7 81.8 79.4 81.2 79.2 78.4 81.3
3 1.5 86.4 83.2 82.6 82.6 78.3 81.1 79.4 83 84.9 87 84.1 86.3 85 83.4 86 82.3 82 83.3
4 1.75 88.9 85.4 84.7 85.4 80.3 84.4 82 85.8 87.9 89.6 88.5 88.8 86.4 87.6 89.2 85.4 84 86.5
5 2 91.4 87.6 86.7 88.1 82.2 87.4 84.2 88.4 90 91.4 90.6 92.2 87.1 91.4 92.2 88.4 85.9 88.9
6 3 101. 97 94.2 98.6 89.4 94 93.2 97.3 97.3 100. 96.6 99.3 96.2 101. 101. 101 95.6 99.4
7 4 110. 105. 100. 104. 96.9 102. 102. 107. 103. 111 105. 106. 104 106. 110. 107. 102. 104.
8 5 116. 112. 107. 111 104. 109. 109 113. 108. 118. 112 113. 111 113. 117. 115. 109. 112.
9 6 122. 119. 112. 116. 111. 116. 117. 119. 114. 126. 119. 120. 117. 120. 122. 121. 118. 119
10 7 130 125 119. 123. 116. 122. 123. 126. 120. 131. 125. 127. 124. 129. 130. 128 125. 128
Мои извинения за отсутствие точности в десятичных разрядах. Данные представлены в виде таблицы таблиц, которая, похоже, не отвечает на обычные команды R для большей точности. Для согласованности, возможно, было бы лучше просто игнорировать все строки после строки 5, поскольку строки 1 - 5 отображают полную точность, которая присутствует в исходных данных.
В полных данных, возраст
> Children$age
[1] 1.00 1.25 1.50 1.75 2.00 3.00 4.00 5.00 6.00 7.00 8.00 8.50 9.00 9.50 10.00 10.50 11.00 11.50 12.00 12.50
[21] 13.00 13.50 14.00 14.50 15.00 15.50 16.00 16.50 17.00 17.50 18.00
И есть 39 мальчиков, перечисленных в том же широком формате данных, что и в приведенном выше примере.
1 ответ
Отказ от ответственности: Для начала давайте подберем (неиерархическую) модель нелинейного роста с использованием Stan.
Читаем в примере данных.
library(tidyverse); df <- read.table(text = " age boy01 boy02 boy03 boy04 boy05 boy06 boy07 boy08 boy09 boy10 boy11 boy12 boy13 boy14 boy15 boy16 boy17 boy18 1 1 81.3 76.2 76.8 74.1 74.2 76.8 72.4 73.8 75.4 78.8 76.9 81.6 78 76.4 76.4 76.2 75 79.7 2 1.25 84.2 80.4 79.8 78.4 76.3 79.1 76 78.7 81 83.3 79.9 83.7 81.8 79.4 81.2 79.2 78.4 81.3 3 1.5 86.4 83.2 82.6 82.6 78.3 81.1 79.4 83 84.9 87 84.1 86.3 85 83.4 86 82.3 82 83.3 4 1.75 88.9 85.4 84.7 85.4 80.3 84.4 82 85.8 87.9 89.6 88.5 88.8 86.4 87.6 89.2 85.4 84 86.5 5 2 91.4 87.6 86.7 88.1 82.2 87.4 84.2 88.4 90 91.4 90.6 92.2 87.1 91.4 92.2 88.4 85.9 88.9 6 3 101. 97 94.2 98.6 89.4 94 93.2 97.3 97.3 100. 96.6 99.3 96.2 101. 101. 101 95.6 99.4 7 4 110. 105. 100. 104. 96.9 102. 102. 107. 103. 111 105. 106. 104 106. 110. 107. 102. 104. 8 5 116. 112. 107. 111 104. 109. 109 113. 108. 118. 112 113. 111 113. 117. 115. 109. 112. 9 6 122. 119. 112. 116. 111. 116. 117. 119. 114. 126. 119. 120. 117. 120. 122. 121. 118. 119 10 7 130 125 119. 123. 116. 122. 123. 126. 120. 131. 125. 127. 124. 129. 130. 128 125. 128", header = T, row.names = 1); df <- df %>% gather(boy, height, -age);Определим модель Стэна.
model <- " data { int N; // Number of observations real y[N]; // Height real t[N]; // Time } parameters { real<lower=0,upper=1> s[2]; real h_theta; real theta; real sigma; } transformed parameters { vector[N] mu; real h1; h1 = max(y); for (i in 1:N) mu[i] = h1 - 2 * (h1 - h_theta) / (exp(s[1] * (t[i] - theta)) + (exp(s[2] * (t[i] - theta)))); } model { // Priors s ~ cauchy(0, 2.5); y ~ normal(mu, sigma); } "Здесь мы рассмотрим слабоинформативные (регуляризирующие) априоры на
s[1]а такжеs[2],Подгоните модель к данным.
library(rstan); options(mc.cores = parallel::detectCores()); rstan_options(auto_write = TRUE); model <- stan( model_code = model, data = list( N = nrow(df), y = df$height, t = df$age), iter = 4000);Сводка 6 параметров модели:
summary(model, pars = c("h1", "h_theta", "theta", "s", "sigma"))$summary # mean se_mean sd 2.5% 25% 50% #h1 131.0000000 0.000000000 0.0000000 131.0000000 131.0000000 131.0000000 #h_theta 121.6874553 0.118527828 2.7554944 115.4316738 121.1654809 122.2134014 #theta 6.5895553 0.019738319 0.5143429 5.4232740 6.4053479 6.6469534 #s[1] 0.7170836 0.214402086 0.3124318 0.1748077 0.3843143 0.8765256 #s[2] 0.3691174 0.212062373 0.3035039 0.1519308 0.1930381 0.2066811 #sigma 3.1524819 0.003510676 0.1739904 2.8400096 3.0331962 3.1411533 # 75% 97.5% n_eff Rhat #h1 131.0000000 131.0000000 8000.000000 NaN #h_theta 123.0556379 124.3928800 540.453594 1.002660 #theta 6.8790801 7.3376348 679.024115 1.002296 #s[1] 0.9516115 0.9955989 2.123501 3.866466 #s[2] 0.2954409 0.9852540 2.048336 6.072550 #sigma 3.2635849 3.5204101 2456.231113 1.001078Так что это значит? От
Rhatзначения дляs[1]а такжеs[2]Вы можете видеть, что есть проблемы с конвергенцией для этих двух параметров. Это связано с тем, чтоs[1]а такжеs[2]неразличимы: они не могут быть оценены одновременно. Более сильная регуляризация доs[1]а такжеs[2]вероятно, будет вести один изsпараметры к нулю.
Я не уверен, что понимаю смысл s[1] а также s[2], С точки зрения статистического моделирования, вы не можете получить оценки для обоих параметров в простой нелинейной модели роста, которую мы рассматриваем.
Обновить
Как и было обещано, это обновление. Это превращается в довольно длинный пост, я постарался прояснить ситуацию, добавив дополнительные пояснения.
Предварительные комментарии
С помощью
positive_orderedкак тип данных дляsимеет существенное значение с точки зрения сходимости решений. Мне не понятно, почему это так, и я не знаю, как реализует Стэнpositive_ordered, но это работает.В этом иерархическом подходе мы частично объединяем данные о высоте для всех мальчиков, учитывая
h1 ~ normal(mu_h1, sigma_h1), с априорами по гиперпараметрамmu_h1 ~ normal(max(y), 10)с половиной Коши доsigma_h1 ~ cauchy(0, 10)(это наполовину Коши, потому чтоsigmaобъявлен какreal<lower=0>).Честно говоря, я не уверен в интерпретации (и интерпретируемости) некоторых параметров. Оценки за
h_1а такжеh_thetaочень похожи, и в некотором роде компенсируют друг друга. Я полагаю, что это создает некоторые проблемы сходимости при подборе модели, но, как вы можете видеть ниже,Rhatзначения кажутся в порядке. Тем не менее, поскольку я недостаточно знаю модель, данные и их контекст, я по-прежнему скептически отношусь к интерпретируемости этих параметров. Расширение модели путем превращения некоторых других параметров в параметры группового уровня является простым с точки зрения статистического моделирования; однако я предполагаю, что трудности возникнут из-за неразличимости и отсутствия интерпретируемости.
Все эти пункты в стороне, это должно дать вам практический пример того, как реализовать иерархическую модель.
Модель Стэн
model_code <- "
data {
int N; // Number of observations
int J; // Number of boys
int<lower=1,upper=J> boy[N]; // Boy of observation
real y[N]; // Height
real t[N]; // Time
}
parameters {
real<lower=0> h1[J];
real<lower=0> h_theta;
real<lower=0> theta;
positive_ordered[2] s;
real<lower=0> sigma;
// Hyperparameters
real<lower=0> mu_h1;
real<lower=0> sigma_h1;
}
transformed parameters {
vector[N] mu;
for (i in 1:N)
mu[i] = h1[boy[i]] - 2 * (h1[boy[i]] - h_theta) / (exp(s[1] * (t[i] - theta)) + (exp(s[2] * (t[i] - theta))));
}
model {
h1 ~ normal(mu_h1, sigma_h1); // Partially pool h1 parameters across boys
mu_h1 ~ normal(max(y), 10); // Prior on h1 hyperparameter mu
sigma_h1 ~ cauchy(0, 10); // Half-Cauchy prior on h1 hyperparameter sigma
h_theta ~ normal(max(y), 2); // Prior on h_theta
theta ~ normal(max(t), 2); // Prior on theta
s ~ cauchy(0, 1); // Half-Cauchy priors on s[1] and s[2]
y ~ normal(mu, sigma);
}
"
Подводя итог: мы объединяем данные о росте от всех мальчиков, чтобы улучшить оценки на уровне группы (т. Е. Мальчиков), моделируя параметр роста взрослых как h1 ~ normal(mu_h1, sigma_h1)где гиперпараметры mu_h1 а также sigma_h1 охарактеризовать нормальное распределение значений роста взрослых среди всех мальчиков. Мы выбираем слабоинформативные априорные значения для гиперпараметров и выбираем слабоинформативные априорные значения для всех оставшихся параметров, аналогично первому примеру полного пула.
Подходит модель
# Fit model
fit <- stan(
model_code = model_code,
data = list(
N = nrow(df),
J = length(unique(df$boy)),
boy = df$boy,
y = df$height,
t = df$age),
iter = 4000)
Извлечь резюме
Мы извлекаем оценки параметров для всех параметров; обратите внимание, что у нас сейчас столько h1 параметры как есть группы (т.е. мальчики).
# Get summary
summary(fit, pars = c("h1", "h_theta", "theta", "s", "sigma"))$summary
# mean se_mean sd 2.5% 25% 50%
#h1[1] 142.9406153 0.1046670943 2.41580757 138.4272280 141.2858391 142.909765
#h1[2] 143.7054020 0.1070466445 2.46570025 139.1301456 142.0233342 143.652657
#h1[3] 144.0352331 0.1086953809 2.50145442 139.3982034 142.3131167 143.971473
#h1[4] 143.8589955 0.1075753575 2.48015745 139.2689731 142.1666685 143.830347
#h1[5] 144.7359976 0.1109871908 2.55284812 140.0529359 142.9917503 144.660586
#h1[6] 143.9844938 0.1082691127 2.49497990 139.3378948 142.2919990 143.926931
#h1[7] 144.3857221 0.1092604239 2.51645359 139.7349112 142.6665955 144.314645
#h1[8] 143.7469630 0.1070594855 2.46860328 139.1748700 142.0660983 143.697302
#h1[9] 143.6841113 0.1072208284 2.47391295 139.0885987 141.9839040 143.644357
#h1[10] 142.9518072 0.1041206784 2.40729732 138.4289207 141.3114204 142.918407
#h1[11] 143.5352502 0.1064173663 2.45712021 138.9607665 141.8547610 143.483157
#h1[12] 143.0941582 0.1050061258 2.42894673 138.5579378 141.4295430 143.055576
#h1[13] 143.6194965 0.1068494690 2.46574352 138.9426195 141.9412820 143.577920
#h1[14] 143.4477182 0.1060254849 2.44776536 138.9142081 141.7708660 143.392231
#h1[15] 143.1415683 0.1049131998 2.42575487 138.6246642 141.5014391 143.102219
#h1[16] 143.5686919 0.1063594201 2.45328456 139.0064573 141.8962853 143.510276
#h1[17] 144.0170715 0.1080567189 2.49269747 139.4162885 142.3138300 143.965127
#h1[18] 143.4740997 0.1064867748 2.45545200 138.8768051 141.7989566 143.426211
#h_theta 134.3394366 0.0718785944 1.72084291 130.9919889 133.2348411 134.367152
#theta 8.2214374 0.0132434918 0.45236221 7.4609612 7.9127800 8.164685
#s[1] 0.1772044 0.0004923951 0.01165119 0.1547003 0.1705841 0.177522
#s[2] 1.6933846 0.0322953612 1.18334358 0.6516669 1.1630900 1.463148
#sigma 2.2601677 0.0034146522 0.13271459 2.0138514 2.1657260 2.256678
# 75% 97.5% n_eff Rhat
#h1[1] 144.4795105 147.8847202 532.7265 1.008214
#h1[2] 145.2395543 148.8419618 530.5599 1.008187
#h1[3] 145.6064981 149.2080965 529.6183 1.008087
#h1[4] 145.4202919 149.0105666 531.5363 1.008046
#h1[5] 146.3200407 150.0701757 529.0592 1.008189
#h1[6] 145.5551778 149.1365279 531.0372 1.008109
#h1[7] 145.9594956 149.5996605 530.4593 1.008271
#h1[8] 145.3032680 148.8695637 531.6824 1.008226
#h1[9] 145.2401743 148.7674840 532.3662 1.008023
#h1[10] 144.4811712 147.9218834 534.5465 1.007937
#h1[11] 145.1153635 148.5968945 533.1235 1.007988
#h1[12] 144.6479561 148.0546831 535.0652 1.008115
#h1[13] 145.1660639 148.6562172 532.5386 1.008138
#h1[14] 144.9975197 148.5273804 532.9900 1.008067
#h1[15] 144.6733010 148.1130207 534.6057 1.008128
#h1[16] 145.1163764 148.6027096 532.0396 1.008036
#h1[17] 145.5578107 149.2014363 532.1519 1.008052
#h1[18] 145.0249329 148.4886949 531.7060 1.008055
#h_theta 135.4870338 137.6753254 573.1698 1.006818
#theta 8.4812339 9.2516700 1166.7226 1.002306
#s[1] 0.1841457 0.1988365 559.9036 1.005333
#s[2] 1.8673249 4.1143099 1342.5839 1.001562
#sigma 2.3470429 2.5374239 1510.5824 1.001219
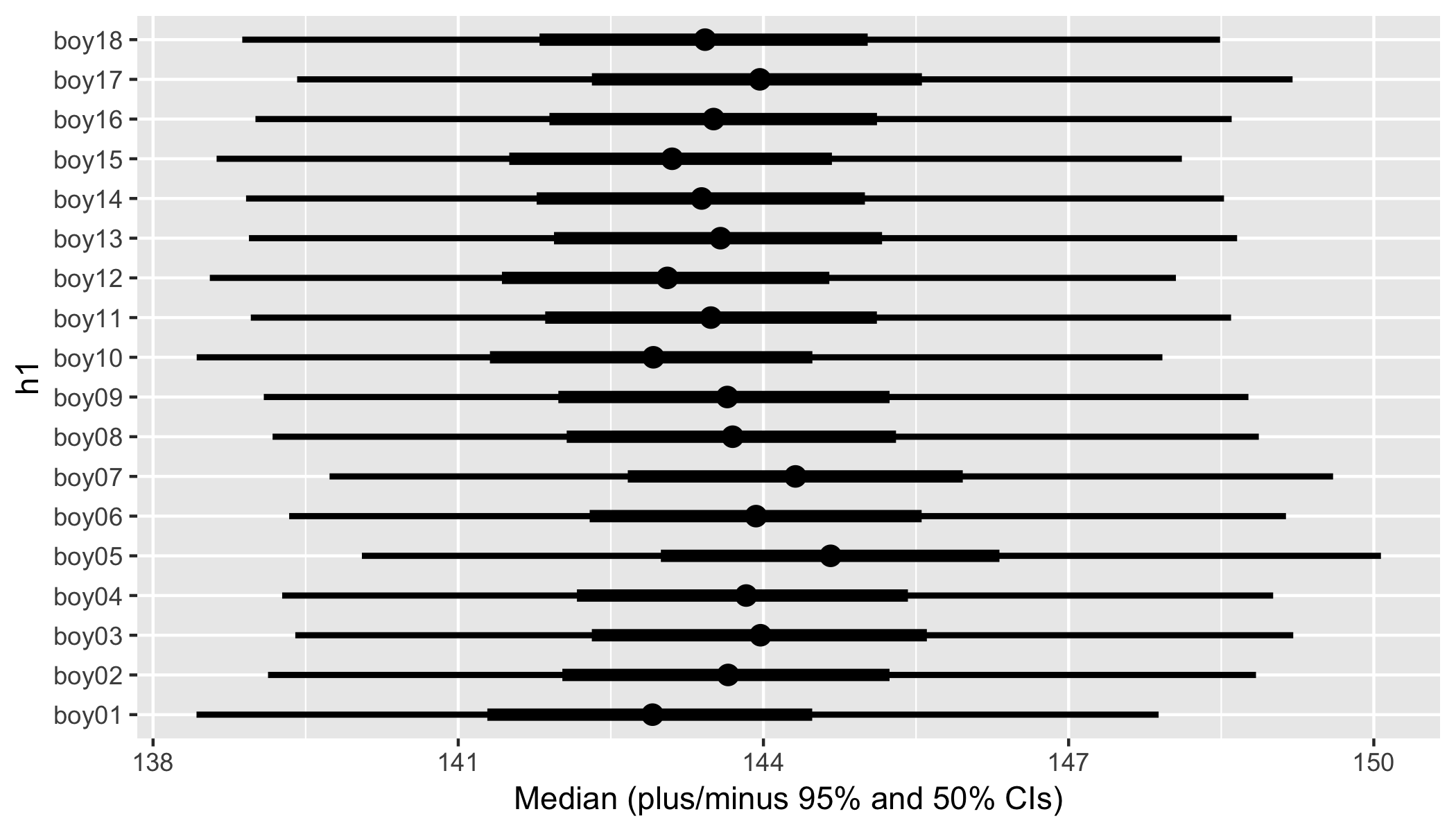
Визуализируйте оценки роста взрослых
Наконец, мы строим оценки роста взрослых h_1 для всех мальчиков, включая 50% и 97% доверительные интервалы.
# Plot h1 values
summary(fit, pars = c("h1"))$summary %>%
as.data.frame() %>%
rownames_to_column("Variable") %>%
mutate(
Variable = gsub("(h1\\[|\\])", "", Variable),
Variable = df$key[match(Variable, df$boy)]) %>%
ggplot(aes(x = `50%`, y = Variable)) +
geom_point(size = 3) +
geom_segment(aes(x = `2.5%`, xend = `97.5%`, yend = Variable), size = 1) +
geom_segment(aes(x = `25%`, xend = `75%`, yend = Variable), size = 2) +
labs(x = "Median (plus/minus 95% and 50% CIs)", y = "h1")