Учитывая один произвольный единичный вектор, каков наилучший метод для вычисления произвольного ортогонального единичного вектора?
По сути, тот же вопрос был задан здесь, но не в контексте программирования. Предлагаемое решение - взять {y, -x, 0 }. Это будет работать для всех векторов, которые имеют компонент x или y, но завершается ошибкой, если вектор равен + или - {0, 0, 1 }. В этом случае мы бы получили {0, 0, 0 }.
Мое текущее решение (в C++):
// floating point comparison utilizing epsilon
bool is_equal(float, float);
// ...
vec3 v = /* some unit length vector */
// ...
// Set as a non-parallel vector which we will use to find the
// orthogonal vector. Here we choose either the x or y axis.
vec3 orthog;
if( is_equal(v.x, 1.0f) )
orthog.set(1.0f, 0.0f, 0.0f);
else
orthog.set(0.0f, 1.0f, 0.0f);
// Find orthogonal vector
orthog = cross(v, orthog);
orthog.normalize();
Этот метод работает, но я чувствую, что может быть лучший метод, и мои поиски больше ничего не показывают.
[РЕДАКТИРОВАТЬ]
Просто для забавы я сделал быстрый код наивных реализаций каждого из предложенных ответов в C++ и убедился, что все они работают (хотя некоторые не всегда возвращают единичный вектор естественным образом, я добавил вызов noramlize(), где это необходимо).
Моя оригинальная идея:
vec3 orthog_peter(vec3 const& v)
{
vec3 arbitrary_non_parallel_vec = v.x != 1.0f ? vec3(1.0, 0.0f, 0.0f) : vec3(0.0f, 1.0f, 0.0f);
vec3 orthog = cross(v, arbitrary_non_parallel_vec);
return normalize( orthog );
}
vec3 orthog_robert(vec3 const& v)
{
vec3 orthog;
if(v.x == 0.0f && v.y == 0.0f)
orthog = vec3(1.0f, 1.0f, 0.0f);
else if(v.x == 0.0f)
orthog = vec3(1.0f, v.z / v.y, 1.0f);
else if(v.y == 0.0f)
orthog = vec3(-v.z / v.x, 1.0f, 1.0f);
else
orthog = vec3(-(v.z + v.y) / v.x, 1.0f, 1.0f);
return normalize(orthog);
}
// NOTE: u and v variable names are swapped from author's example
vec3 orthog_abhishek(vec3 const& v)
{
vec3 u(1.0f, 0.0f, 0.0f);
float u_dot_v = dot(u, v);
if(abs(u_dot_v) != 1.0f)
return normalize(u + (v * -u_dot_v));
else
return vec3(0.0f, 1.0f, 0.0f);
}
vec3 orthog_dmuir(vec3 const& v)
{
float length = hypotf( v.x, hypotf(v.y, v.z));
float dir_scalar = (v.x > 0.0) ? length : -length;
float xt = v.x + dir_scalar;
float dot = -v.y / (dir_scalar * xt);
return vec3(
dot * xt,
1.0f + dot * v.y,
dot * v.z);
};
4 ответа
Ну, вот один из способов сделать это. Пусть задан вектор (a, b, c). Решите уравнение (a, b, c) точка (aa, bb, cc) = 0 для aa, bb и cc (и убедитесь, что aa, bb и cc не все равны нулю), поэтому (aa, bb, cc) ортогональна (а, б, в). Я использовал Maxima ( http://maxima.sf.net/), чтобы решить это.
(%i42) solve ([a, b, c] . [aa, bb, cc] = 0, [aa, bb, cc]), a=0, b=0;
(%o42) [[aa = %r19, bb = %r20, cc = 0]]
(%i43) solve ([a, b, c] . [aa, bb, cc] = 0, [aa, bb, cc]), a=0;
%r21 c
(%o43) [[aa = %r22, bb = - ------, cc = %r21]]
b
(%i44) solve ([a, b, c] . [aa, bb, cc] = 0, [aa, bb, cc]), b=0;
%r23 c
(%o44) [[aa = - ------, bb = %r24, cc = %r23]]
a
(%i45) solve ([a, b, c] . [aa, bb, cc] = 0, [aa, bb, cc]);
%r25 c + %r26 b
(%o45) [[aa = - ---------------, bb = %r26, cc = %r25]]
a
Обратите внимание, что сначала я решил частные случаи (a = 0 и b = 0, или a = 0, или b = 0), так как найденные решения не являются действительными для некоторых компонентов, равных нулю. Переменные%r, которые появляются, являются произвольными константами. Я установлю их равными 1, чтобы получить некоторые конкретные решения.
(%i52) subst ([%r19 = 1, %r20 = 1], %o42);
(%o52) [[aa = 1, bb = 1, cc = 0]]
(%i53) subst ([%r21 = 1, %r22 = 1], %o43);
c
(%o53) [[aa = 1, bb = - -, cc = 1]]
b
(%i54) subst ([%r23 = 1, %r24 = 1], %o44);
c
(%o54) [[aa = - -, bb = 1, cc = 1]]
a
(%i55) subst ([%r25 = 1, %r26 = 1], %o45);
c + b
(%o55) [[aa = - -----, bb = 1, cc = 1]]
a
Надеюсь это поможет. Удачи и продолжайте в том же духе.
Другой способ - использовать отражатели для домохозяек.
Мы можем найти отражатель Q, который отображает наш вектор кратным (1,0,0). Применение Q к (0,1,0) даст вектор, перпендикулярный нашему вектору. Одним из преимуществ этого метода является то, что он применяется к любому количеству измерений; другое состоит в том, что мы можем получить другой вектор (ы) перпендикулярно оригиналу и новому: применить Q к (0,0,1). Это может показаться сложным, но вот код C для 3d (xp,yp,zp - обязательный вектор, и имеет длину 1; как написано, все является двойным, но вы можете использовать вместо этого float и использовать hypotf вместо hypot)
l = hypot( x, hypot(y,z));
s = (x > 0.0) ? l : -l;
xt = x + s;
dot = -y/(s*xt);
xp = dot*xt;
yp = 1.0 + dot*y;
zp = dot*z;
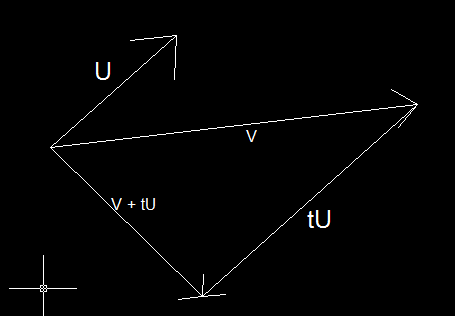
Вам нужно выбрать точку v, которая не равна нулю и не находится на линии, соединяющей начало координат с данным единичным вектором u.
Как уже предлагалось, вы можете выбрать единичный вектор на любой оси, если эта точка удовлетворяет вышеуказанному условию. Если точка u уже лежит на оси, просто выберите любую другую ось для точки v.
Тогда вам нужно решить уравнение (v + tu).u = 0, (просто решить для т)
Конечно, вам нужно будет нормализовать его, чтобы получить вектор ортогональной единицы.
Вот версия C, которая использует доминирующую ось, чтобы дать более детерминированный результат.
Звонящий должен нормализовать результат ortho_v3_v3,
inline int axis_dominant_v3_single(const float vec[3])
{
const float x = fabsf(vec[0]);
const float y = fabsf(vec[1]);
const float z = fabsf(vec[2]);
return ((x > y) ?
((x > z) ? 0 : 2) :
((y > z) ? 1 : 2));
}
/**
* Calculates \a p - a perpendicular vector to \a v
*
* \note return vector won't maintain same length.
*/
void ortho_v3_v3(float p[3], const float v[3])
{
const int axis = axis_dominant_v3_single(v);
assert(p != v);
switch (axis) {
case 0:
p[0] = -v[1] - v[2];
p[1] = v[0];
p[2] = v[0];
break;
case 1:
p[0] = v[1];
p[1] = -v[0] - v[2];
p[2] = v[1];
break;
case 2:
p[0] = v[2];
p[1] = v[2];
p[2] = -v[0] - v[1];
break;
}
}