Выполнение позиционирования вокселей в октрее / квадри

Question

Это то, о чем я думал последние пару часов. Это упражнение ума.

Итак, я узнал, какие октры были сегодня! Очень интересно! Я думал о том, как реализовать октре, разрешенное в вокселе.

Моя самая большая проблема, с которой я не могу сейчас обернуться, это ссылка на позицию в октри.

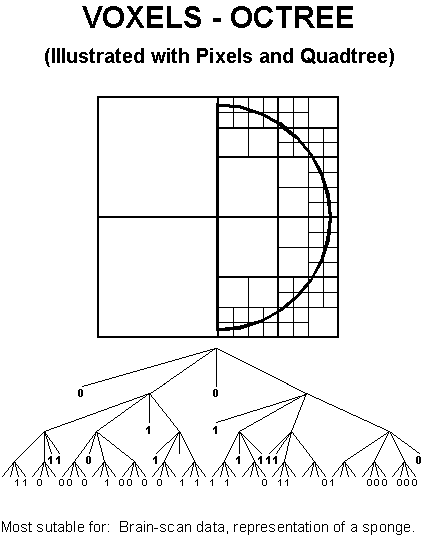
Отказ от ответственности: во-первых, я собираюсь использовать квадри в 2D-плоскости для визуализации своей проблемы. Во-вторых, я не понимаю правильный жаргон здесь, я собираюсь предположить, что любое подразделение в октодереве, которое является родителем, является "ветвью", а любое подразделение, которое является только дочерним (в данном случае это разрешается в вокселе), является лист". В-третьих, я собираюсь пронумеровать каждое пространство в ветви дерева слева направо сверху вниз {1,2,3,4}

Допустим, у меня есть quadtree, которое определяет единицу пространства 16x16. В локации [16,16] у меня хранится воксель.

4->4->4->4

Теперь скажите, что мы добавляем воксель в позицию [4,4]. (Обратите внимание, мы начинаем с нуля)

1->4->1->1
4->4->4->4

Допустим, я хочу проверить [16,8], чтобы увидеть, сохранен ли воксель. Используя предыдущий метод, мы бы технически обошли эти ветви:

4->1->1->1

Однако 4->1 не был выделен никакими данными, поэтому он пуст. (он не подразделяется, потому что не используется).

Мой вопрос становится таким: как я мог быстро пройти через дерево, чтобы найти воксель?

Мой первый и самый простой способ - путешествовать по веткам в формате, который я использовал выше.

// Pseudo-code
Class Quadtree {
Quadtree Parent;
Quadtree c[4]; // children
};

Quadtree test1;
test1.c[4].c[4].c[4].c[4];
Quadtree test2;
test2.c[1].c[4].c[1].c[1];

Проблема в том, что voxelArray[16][16], voxelArray[4][4] или voxelArray[16][8] работают намного быстрее. Использование гораздо большего дерева (256x256) увеличит глубину (с 4 до 8). Где вложенные массивы еще 2 операции с памятью. (Обратите внимание, что для дерева quadtree на самом деле мы использовали бы что-то из аксессора и проверяли, чтобы убедиться, что потомки существуют с условной логикой)

Моя вторая мысль состояла в том, чтобы хранить квадри в качестве самих вокселей. Например, скажем, у нас есть массив 2x2, пустой он будет выглядеть

{0, 0, 0, 0}

В позиции [1,1] мы добавим воксель, и он станет

{0, 0, 0, 1}

Если бы мы хранили квадри, это выглядело бы примерно так

{1/*q*/, 0, 0, 0, 1}

Возьми это к 4х4 и

{0/*q*/, 0, 0, 0, 
 0/*q*/, 0, 0, 0, 
 0/*q*/, 0, 0, 0, 
 1/*q*/, 0, 0, 1}

Хотя теперь вы можете получить доступ к данным напрямую, вы потеряли компактность памяти quadtree и по-прежнему выполняете много логических операций. ИМО, это будет хорошо работать, только если у вас большие области 0 и небольшие группы 1.

Храня воксели в дереве квадро / дерево, вы получаете производительность при цикле их всех, но теряете производительность при непосредственном доступе к ним.

Answer 1

Вы можете вычислить quadkey и затем хешировать каждый воксел. Идея состоит в том, чтобы уменьшить размерную сложность. Вы можете посмотреть, например, на гамильтонову траекторию или кривую z или кривую Гильберта Этот путь полностью пересекает плоскость, но технически он все еще является кривой.

Answer 2

Это скорее расширенный комментарий, чем ответ. Это может быть полезно для вас, хотя. Или это не так. Ваш пример:

{0, 0, 0, 0}

не иллюстрирует пустое quadtree, оно иллюстрирует quadtree, в котором все 4 квадранта имеют значение 0 на первом (и единственном) уровне. Это:

{}

иллюстрирует пустое дерево quadtree. Это:

{0, 0, 0, {1,0,1,0}}

иллюстрирует квадродерево, в котором все 3 квадранта равны 0, а четвертый - шахматная доска (хотя и небольшая). Это:

{{1,{1,0,0,0},0,{1,1,1,{0,0,0,1}}}, 0, 0, {1,0,1,0}}

начинает становиться хитрее, но вы уже поняли мой дрейф.

На некоторых языках (например, Lisp, Matlab, Mathematica) эти иллюстрации могут быть непосредственно реализованы и обработаны. Во многих языках вы бы реализовали квадродерево как набор указателей и / или значений.