Если поиск A* с эвристическим евклидовым расстоянием допускает диагональные перемещения, будет ли он по-прежнему оптимальным?

Question

Так что, если у меня есть поиск A* в 10x10 лабиринте с 10 препятствиями, и я позволил диагональные перемещения в этом, будет ли он все еще оптимальным?

Мой ответ заключается в том, что он все равно будет оптимальным, и это потому, что Евклидово расстояние уже вычисляет расстояние по прямой линии между двумя точками, так что оно в любом случае пересекает пространство поиска по диагонали, так что я не думаю, что это будет иметь значение или это может даже сделать его лучше? Не уверен, правильно ли я думаю.

Answer 1

Это зависит от стоимости диагональных ходов.

Рассмотрим ситуацию с единообразными затратами: стоимость диагонального перемещения равна стоимости недиагонального ( расстояние Чебышева).

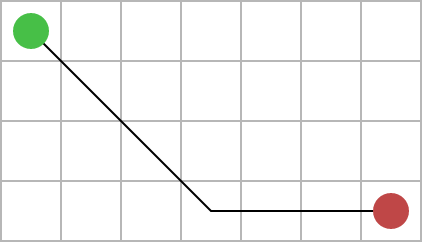
В этом случае расстояние между зеленой и красной точкой 6, В общем:

def chebyshev_distance(node):
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return max(dx, dy)

тогда как евклидово расстояние эвристическое:

def heuristic(node):
    dx = abs(node.x - goal.x)
    dy = abs(node.y - goal.y)
    return sqrt(dx * dx + dy * dy)

дает heuristic ≅ 6.71 и переоценивает стоимость пути, что приводит к недопустимой эвристике (может не найти оптимальный путь).

В общем:

max (| d _x |, | d _y |) = | Max | = sqrt(макс. ²) ≤ sqrt(макс. ² + min ²) = sqrt(д _х ² + д _у ²)