Простой алгоритм парковки
Я ищу простой алгоритм парковки для игры.
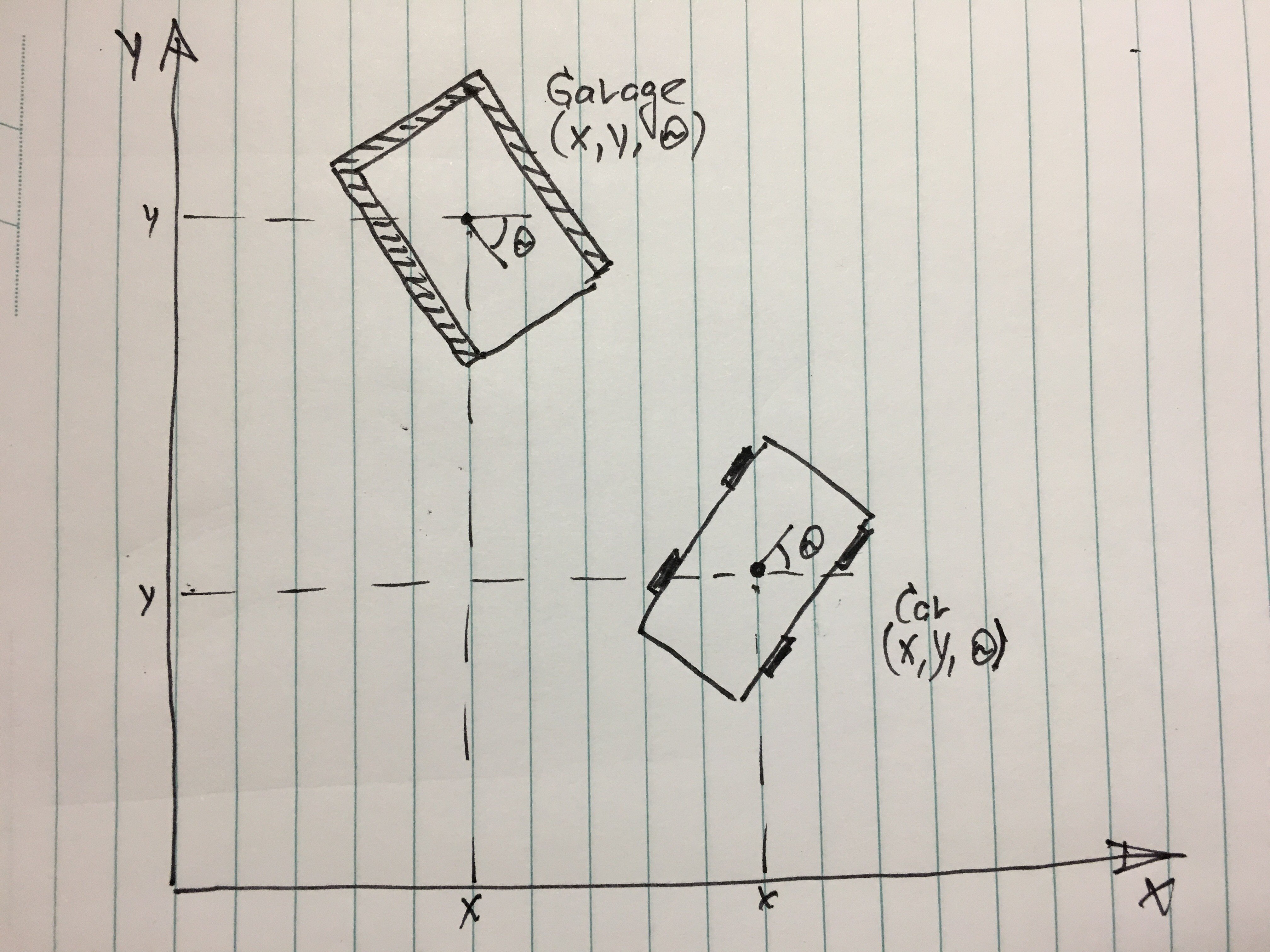
Положение автомобиля и гаража, каждый из которых определяется 3 номера (x, y, theta), куда x а также y - центр объекта и theta - угол между осью объекта и осью X.
Движение автомобиля упрощено - это точка (нет необходимости рассчитывать точное движение шины), которая может двигаться с fixed speed назад и вперед или поверните по кругу с радиусом R (радиус поворота может быть фиксированным или гибким - не имеет значения - мне подойдет любой вариант) и имеет no inertia or acceleration,
В гараже 3 стены, которые не должны касаться машины. Для столкновения можно использовать точные размеры, но для простоты столкновение проверяется путем измерения углов между автомобилем и гаражом и расстоянием между осью автомобиля и центром гаража. Когда автомобиль и гараж находятся достаточно близко (расстояние между центрами меньше некоторой постоянной CloseEnough) столкновение проверено (alpha, d) < (maxAlpha, maxDistance)
Мир, имитируемый галочками, мы берем на себя нынешнее управление автомобилем - moving direction вперед или назад и turning angle и рассчитать автомобиль следующей позиции.
Алгоритм должен выдавать серию команд управления, например [forward, left], [forward, left], [backward, straight], [forward, right],
Ничего страшного, если это будет итеративно и будет производить по одной команде за раз - тогда проверьте, что происходит на следующем тике, и произведите еще одну. Он может попросить механизм моделирования смоделировать и создать новые координаты с помощью управляющей команды или использовать механизм моделирования, чтобы опробовать несколько вариантов и выбрать лучший.
Кроме того, это нормально, если он делает это с помощью ряда приближенных движений, как если бы он попытался один раз - пропустил, попробовал в другой раз - приблизился и в третий раз - наконец припарковался (но это должно быть более или менее разумно и не делать десятки или сотни трюков) туда и обратно итераций).
2 ответа
Есть несколько изломов, которые нужно решить, например, какая точность требуется для успешного дока, и какая точность позволяют "галочки". Вам придется экспериментировать. Но вот общий подход:
Без потери общности предположим, что машина движется по прямым линиям и окружностям с минимальным радиусом. (Большие круги дадут более короткую и мягкую езду, но оставим это на потом.) На практике это будет означать чередование линии-круга-линии-круга-линии...
Конечная цель - ехать прямо в гараж.
Цель до этого ("предпоследняя") - попасть на один из кругов, касающихся этого пути, как можно ближе к гаражу. Так, если гараж находится в (0,0,0), круги центрированы в (0, +/1r). В общем, если гараж находится в точке (x, y, θ), окружности центрируются в точке (x-/+rsinθ, y+/-rcosθ).
Цель до этого ("antepenultimate"?) Состоит в том, чтобы попасть из одного из кругов, на котором уже находится машина (влево или вправо), в линию, касающуюся как этого круга, так и целевого круга.
Цель до этого состоит в том, чтобы обойти гараж, если это необходимо, чтобы машина могла выполнять уже описанные движения, не ударяя по ней. Один из способов решения этой проблемы - нарисовать круг с центром в каждом углу гаража и переходить от круга к кругу.
Этого достаточно?
Вам может помочь путь Дубинса, как упоминалось ранее, использование кругов, радиус которых основан на самой узкой кривизне автомобиля и касательных линиях, соединяющих эти круги, основная цель - найти, где разместить эти необходимые круги на вашей карте, и когда они у вас появятся, вы почти готово, я думаю!