Дифракция Френеля в два этапа

Я написал короткий файл сценария matlab, который, как предполагается, должен выполнять распространение (дифракцию) Френеля, чтобы при заданном поле ввода U0 оно сообщало вам, как выглядит поле после расстояния z0. Я сравнил результат с результатами учебника, и похоже, что моя программа работает нормально. Проблема в том, что если я попытаюсь сделать два шага распространения вместо одного. т.е. вместо одной итерации программы для распространения на расстояние z0, я беру две итерации программы для распространения на расстояние z0/2 каждая. Тогда я получаю полную чушь и не могу понять, в чем проблема. Любой совет будет принят с большой благодарностью. Вот код:

function U = fresnel_advance (U0, dx, dy, z, lambda)
% The function receives a field U0 at wavelength lambda
% and returns the field U after distance z, using the Fresnel
% approximation. dx, dy, are spatial resolution.

k=2*pi/lambda;
[ny, nx] = size(U0); 

Lx = dx * nx;
Ly = dy * ny;

dfx = 1./Lx;
dfy = 1./Ly;

u = ones(nx,1)*((1:nx)-nx/2)*dfx;    
v = ((1:ny)-ny/2)'*ones(1,ny)*dfy;   

O = fftshift(fft2(U0));

H = exp(1i*k*z).*exp(-1i*pi*lambda*z*(u.^2+v.^2));  

U = ifft2(O.*H);
Источник

3 ответа

Решение

После звонка fft2звоните также fftshift иметь частоту постоянного тока в середине.

Но когда вы звоните ifft2, функция предполагает, что у вас все еще есть частота постоянного тока в (1,1). Таким образом, вы должны вернуться к этому формату, прежде чем делать обратное БПФ.

Таким образом, изменение последней строки U = ifft2(fftshift(O.*H)) может решить проблему.

РЕДАКТИРОВАТЬ

Я только что видел, что Matlab советует использовать ifftshift после fftshift в два раза ifftshift (не могу найти версию, в которой он представлен). Согласно документации, последовательность звонков ifftshift(fftshift(X)) а также ifftshift(fftshift(X)) не эквивалентны в случае нечетных размеров.

Поэтому я думаю, что лучше сделать: U = ifft2(ifftshift(O.*H)) на последнем шаге вашего кода.

Источник

На самом деле проблема заключается в том, как вы запускаете свой fft. Это хорошо объясняется в Fourier Optics and Computational Imaging Khedar Kare, Wiley 2015:

Подходящая последовательность для 2D БПФ на большинстве программных платформ для того, чтобы результат был значимым с физической точки зрения (например, при описании таких явлений, как дифракция), таким образом, задается следующим образом: fftshift(fft2(ifftshift(...))).

В вашем коде вы должны:O = fftshift(fft2(ifftshift(U0)));

Если вас интересует программное обеспечение, разработанное на Python, существует быстро развивающийся набор инструментов Python для оптики, включая дифракцию: PyOptica. В PyOptica волновой фронт можно распространять с помощью:

import astropy.units as u
import numpy as np

import pyoptica as po


wavelength = 500 * u.nm 
pixel_scale = 22 * u.um
npix = 1024

w = 6 * u.mm
h = 3 * u.mm
axis_unit = u.mm

wf = po.Wavefront(wavelength, pixel_scale, npix)
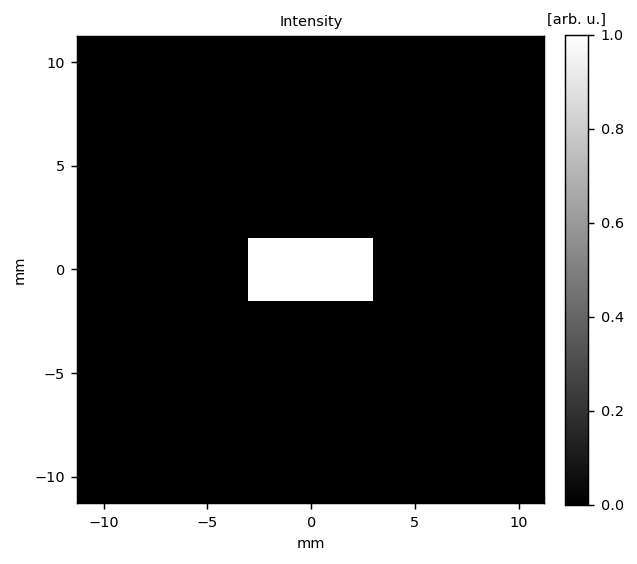
ap = po.RectangularAperture(w, h)
wf = wf * ap
fig_1 = po.plotting.plot_wavefront(wf, 'intensity', axis_unit=axis_unit)

Начальная апертура

Второй шаг - размножить:

f = 50 * u.cm
fs_f = po.FreeSpace(f)
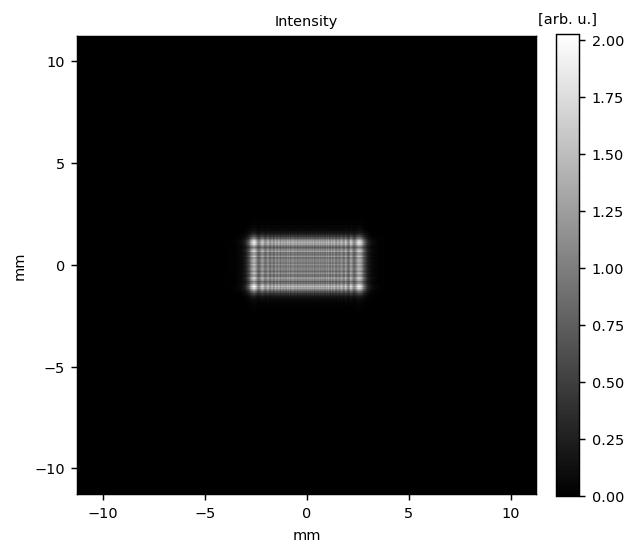
wf_forward = wf * fs_f
fig_2 = po.plotting.plot_wavefront(wf_forward, 'intensity',  axis_unit=axis_unit)

Результаты после размножения

Важно помнить условия выборки для распространения Френеля, а именно: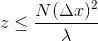введите описание изображения здесь(z <= N (dx) ^ 2 / lambda), где:

  • N - количество пикселей (в одну сторону);
  • dx - размер пикселя;
  • лямбда - длина волны.

Это условие основано на " Computational Fourier Optics: A MATLAB Tutorial by David Voelz, SPIE 2011".

Вы должны реализовать это условие в своем коде. В PyOptica это всегда проверяется перед распространением; если запрошенное расстояние нарушает условие, расстояние распространения разбивается на подшаги.

Источник

Было бы полезно, если бы вы могли опубликовать некоторые примеры входных данных в вашей программе, чтобы продемонстрировать проблему.

Я подозреваю, что проблема может быть связана с тем, что вы не звоните в FFTSHIFT достаточное количество раз. Обычно считается, что центр матрицы оптического поля находится в "начале координат", а FFT2 рассматривает "левый нижний" угол. Поэтому вы должны FFTSHIFT до FFT2, а также после.

Вы должны сделать то же самое для части IFFT2.

РЕДАКТИРОВАТЬ Обоснование добавления двух вызовов в FFTSHIFT: сравните эти два:

N = 512; [x,y] = meshgrid(-1:1/N:(N-1)/N);
mask = (x.*x + y.*y) < 0.001;
figure(1)
imagesc(angle(fftshift(fft2(fftshift(mask)))))
figure(2)
imagesc(angle(fftshift(fft2(mask)))
Источник

Я думаю, что есть ошибка фазового члена. "H = exp (1ik z).Exp (-1i pilambda z * (u. ^ 2 + v. ^ 2));"
должно быть "H = exp (1ik z).exp (-1i pi / lambda / z * (u. ^ 2 + v. ^ 2));"

Источник
Другие вопросы по тегам