Естественная регрессия кубического сплайна с R
Кажется, у меня проблема с splines::ns() функция в R.
Я создал простую пустышку
dat <- data.frame(t <- seq(0, 6, .01),
x <- rnorm(length(t), sd = 1),
y <- 5 + t - x^2 + rnorm(length(t), sd = .33))
lm(y ~ t + I(x^2), data = dat)
library(splines)
lm(y ~ t + ns(x, knots = c(0), Boundary.knots = c(-3, 3)), data = dat)
Хотя первая модель работает нормально, вторая не может правильно идентифицировать перехват. Что мне здесь не хватает?
2 ответа
В этом нет ничего плохого, потому что вы не подходите точно такой же модели, и они даже не эквивалентны.
Чтобы объяснить другой результат, который вы видите, достаточно использовать более простой пример с одной ковариатой x, Мы генерируем данные из квадратичного полинома: 5 + x + x^2Затем подойдет несколько моделей.
set.seed(0)
x <- rnorm(500, mean = 1) ## `x` with non-zero mean
y <- 5 + x + x * x + rnorm(500, sd = 0.5)
library(splines)
fit1 <- lm(y ~ x + I(x^2))
#(Intercept) x I(x^2)
# 4.992 1.032 0.980
fit2 <- lm(y ~ poly(x, degree = 2))
#(Intercept) poly(x, degree = 2)1 poly(x, degree = 2)2
# 7.961 70.198 28.720
fit3 <- lm(y ~ bs(x, degree = 2, df = 2))
#(Intercept) bs(x, degree = 2, df = 2)1 bs(x, degree = 2, df = 2)2
# 6.583 -8.337 20.650
fit4 <- lm(y ~ ns(x, df = 2))
#(Intercept) ns(x, df = 2)1 ns(x, df = 2)2
# 5.523 10.737 21.265
Первые 3 модели не одинаковы с точки зрения параметризации, но они эквивалентны: все они соответствуют квадратичному полиному с 3 степенями свободы. Чтобы увидеть их эквивалентность, мы проверим их подогнанные значения:
sum(abs(fit1$fitted - fit2$fitted))
# [1] 1.54543e-13
sum(abs(fit1$fitted - fit3$fitted))
# [1] 2.691181e-13
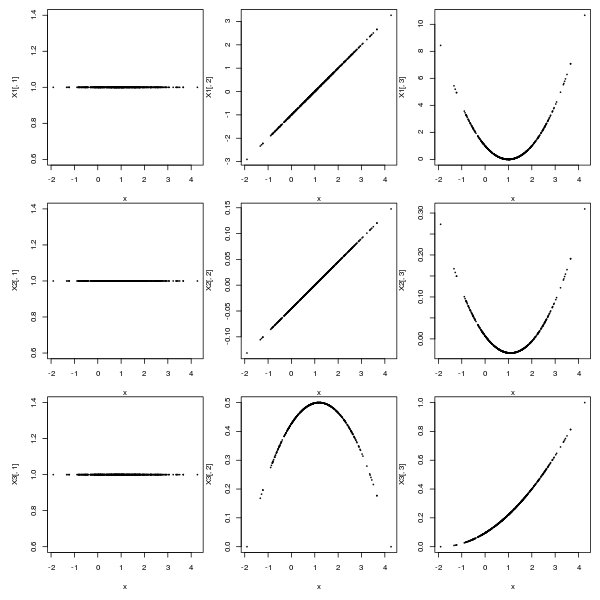
Чтобы увидеть разницу в параметризации, мы рассмотрим матрицу проектирования:
X1 <- model.matrix(~ x + I(x^2))
X2 <- model.matrix(~ poly(x, degree = 2))
X3 <- model.matrix(~ bs(x, degree = 2, df = 2))
par(mfrow = c(3,3), oma = rep.int(1,4), mar = c(4, 4, 0, 0))
plot(x, X1[, 1], cex = 0.2)
plot(x, X1[, 2], cex = 0.2)
plot(x, X1[, 3], cex = 0.2)
plot(x, X2[, 1], cex = 0.2)
plot(x, X2[, 2], cex = 0.2)
plot(x, X2[, 3], cex = 0.2)
plot(x, X3[, 1], cex = 0.2)
plot(x, X3[, 2], cex = 0.2)
plot(x, X3[, 3], cex = 0.2)
Так как матрица дизайна не одинакова (ни в форме, ни в масштабе), у вас не будет одинакового набора коэффициентов. Если вы удивлены, давайте попробуем еще более простой пример:
x1 <- x - mean(x)
test <- lm(y ~ x1 + I(x1^2))
#(Intercept) x1 I(x1^2)
# 7.003 2.991 0.980
sum(abs(fit1$fitted - test$fitted))
# [1] 1.24345e-13
Здесь я только что принял простое преобразование для x, тогда результат другой (но все равно эквивалентный).
4-я модель fit4, подгоняет кубический многочлен с 3 степенями свободы, поэтому он не эквивалентен всем предыдущим моделям. Мы можем проверить установленные значения:
sum(abs(fit1$fitted - fit4$fitted))
# [1] 39.36563
Полностью игнорируя ns(), вы упускаете две вещи:
1) Комментарий выше объясняет, как определить фрейм данных:
t <- seq(0, 6, .01)
x <- rnorm(length(t), sd = 1)
y <- 5 + t - x^2 + rnorm(length(t), sd = .33)
df <- data.frame(t, x, y)
rm(t, x, y)
2) То, как вы называете свои модели:
lm(y ~ t + I(t^2), data=df)
lm(y ~ splines::ns(t, knots = c(0), Boundary.knots = c(-3, 3)), data=df)
Первая модель не правильно определяет, что вы думаете, что она делает.