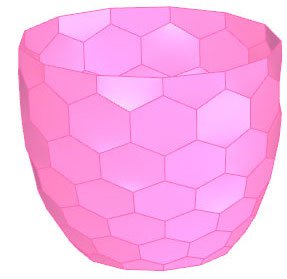
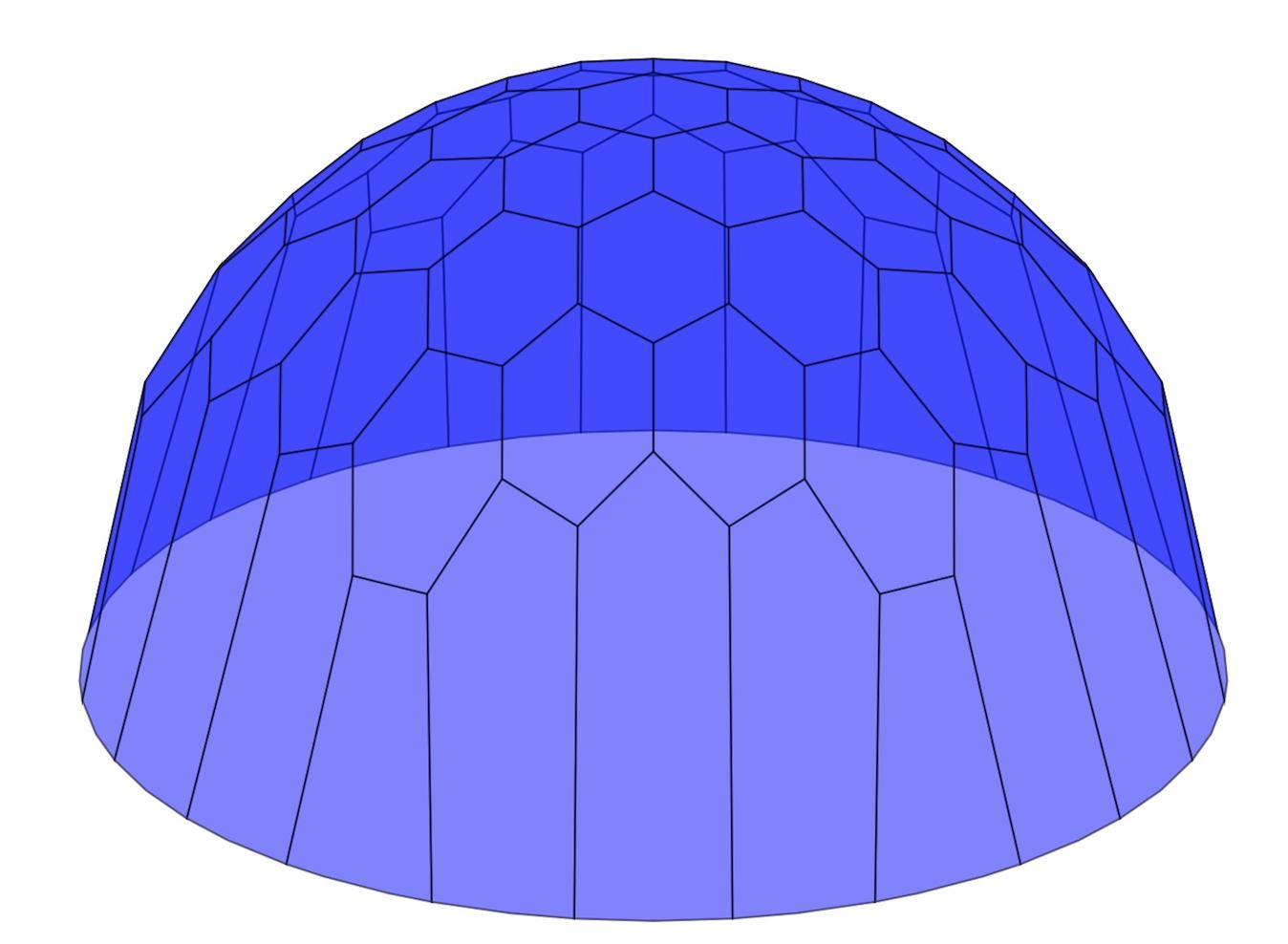
Гексагональная обработка полусферы

Question

Мне нужно иметь гексагональную сетку на сферической поверхности. как показано здесь.

Прямо сейчас я делаю гексагональную сплющенную сетку. 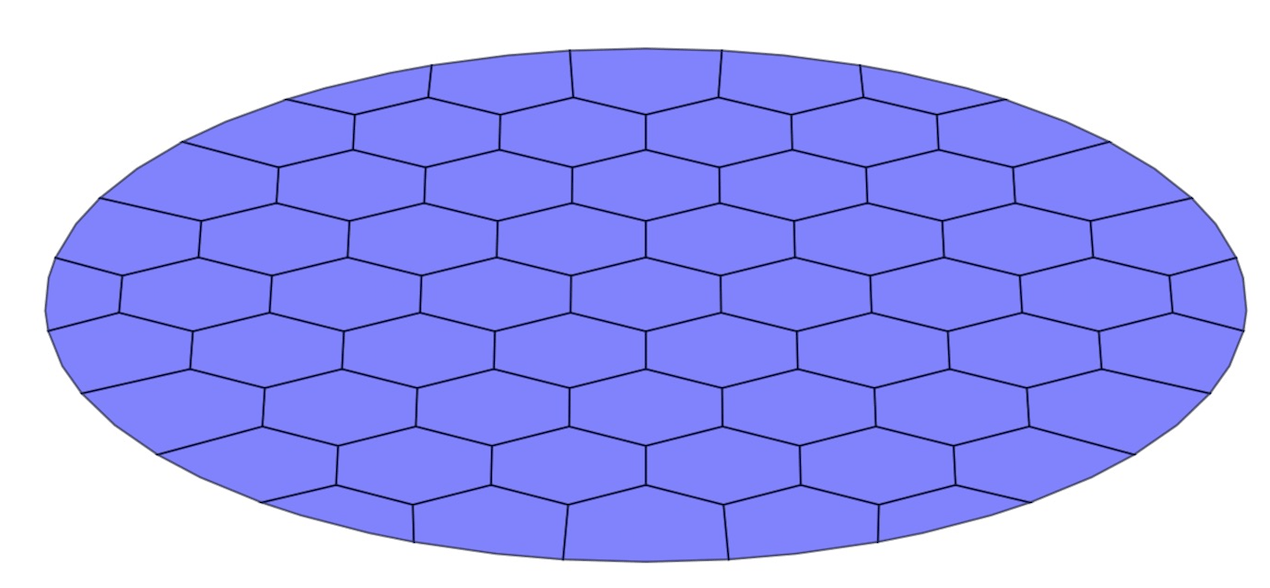и проецируя его на поверхность полушария. Как здесь, но, как вы можете видеть, забавный артефакт - шестиугольники на краю несоразмерно велики. Должен быть лучший способ сделать это так, чтобы все шестиугольники были примерно равны по размеру.

Я попробовал решение, как предложил @spektre, но мой код создавал следующий сюжет.

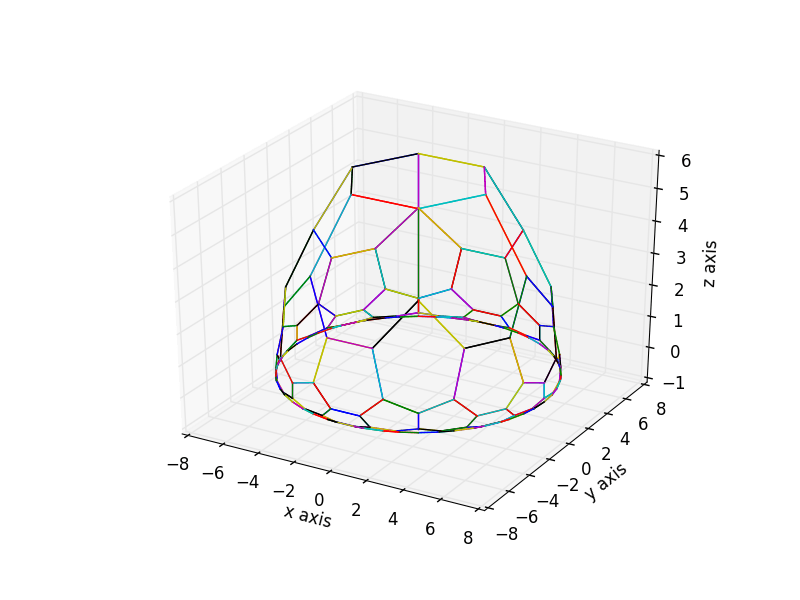я использовал a=sqrt(x*x+y*y)/r * (pi/2) потому что я хотел масштабировать a это идет от [0,r] в z[0,r] такой угол a имеет границы [0,pi/2],

Но только с a=sqrt(x*x+y*y)/r это работает хорошо.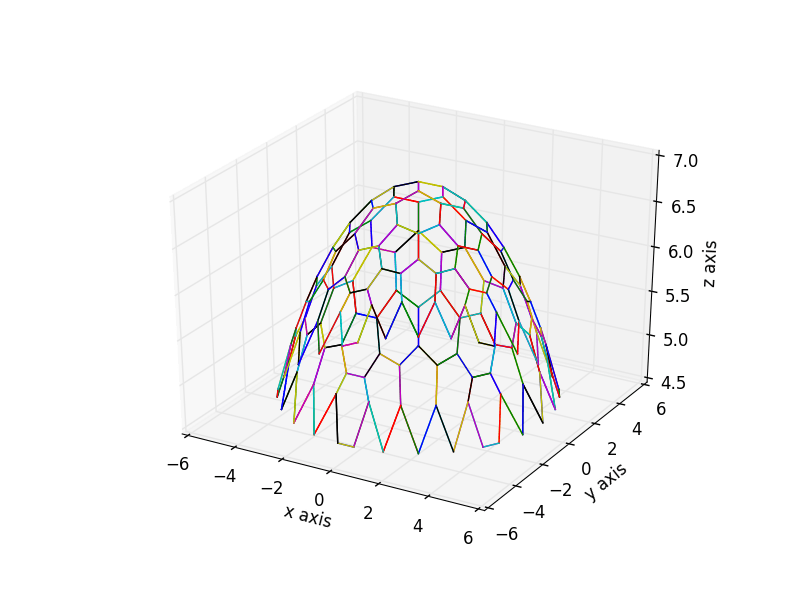

Новая разработка с задачей, Новая проблема

У меня проблема в том, что теперь шестиугольники не равны по форме. Я хочу иметь одинаковую форму (по площади) для них через купол и цилиндр. Я не понимаю, как это сделать?

Answer 1

Вот что я имею в виду:

1. создать плоскую шестигранную сетку на плоскости XY

   центр вашей сетки должен быть центром вашей сферы я выбрал (0,0,0) и размер сетки должен быть как минимум 2* радиус вашей сферы большой.

2. преобразовать плоские координаты в сферические

   так расстояние от (0,0,0) координата точки в плоскости XY - длина дуги, проходящая по поверхности вашей сферы, поэтому, если точка обработки (x,y,z) и радиус сферы r тогда широтное положение на сфере:

   a=sqrt(x*x+y*y)/r;
   

   поэтому мы можем напрямую вычислить координату z:

   z=r*cos(a);
   

   и масштаб x,y к поверхности сферы:

   a=r*sin(a)/sqrt(x*x+y*y);
   x*=a; y*=a;
   

   Если z координата отрицательна, тогда вы пересекли половину сферы и должны обрабатывать по-другому (пропустить шестнадцатеричное или преобразовать в цилиндр или что-то еще)

Вот небольшой пример OpenGL/C++ для этого:

//---------------------------------------------------------------------------
const int _gx=15;           // hex grid size
const int _gy=15;
const int _hy=(_gy+1)<<1;   // hex points size
const int _hx=(_gx+1);
double hex[_hy][_hx][3];    // hex grid points
//---------------------------------------------------------------------------
void hexgrid_init(double r) // set hex[][][] to planar hex grid points at xy plane
    {
    double x0,y0,x,y,z,dx,dy,dz;
    double sx,sy,sz;
    int i,j;
    // hex sizes
    sz=sqrt(8.0)*r/double(_hy);
    sx=sz*cos(60.0*deg);
    sy=sz*sin(60.0*deg);

    // center points arrounf (0,0)
    x0=(0.5*sz)-double(_hy/4)*(sz+sx);
    y0=-double(_hx)*(sy);
    if (int(_gx&1)==0) x0-=sz+sx;
    if (int(_gy&1)==0) y0-=sy; else y0+=sy;

    for (y=y0,i=0;i<_hy;i+=2,y+=sy+sy)
     for (x=x0,j=0;j<_hx;j++,x+=sz)
        {
        hex[i][j][0]=x;
        hex[i][j][1]=y;
        hex[i][j][2]=0.0;
        x+=sz+sx+sx; j++; if (j>=_hx) break;
        hex[i][j][0]=x;
        hex[i][j][1]=y;
        hex[i][j][2]=0.0;
        }

    for (y=y0+sy,i=1;i<_hy;i+=2,y+=sy+sy)
     for (x=x0+sx,j=0;j<_hx;j++,x+=sx+sx+sz)
        {
        hex[i][j][0]=x;
        hex[i][j][1]=y;
        hex[i][j][2]=0.0;
        x+=sz; j++; if (j>=_hx) break;
        hex[i][j][0]=x;
        hex[i][j][1]=y;
        hex[i][j][2]=0.0;
        }

    }
//---------------------------------------------------------------------------
void hexgrid_half_sphere(double r0) // convert planar hex grid to half sphere at (0,0,0) with radius r0
    {
    int i,j;
    double x,y,z,a,l;
    for (i=0;i<_hy;i++)
     for (j=0;j<_hx;j++)
        {
        x=hex[i][j][0];
        y=hex[i][j][1];
        z=hex[i][j][2];
        l=sqrt(x*x+y*y);    // distance from center on xy plane (arclength)
        a=l/r0;             // convert arclength to angle
        z=r0*cos(a);        // compute z coordinate (sphere)
        if (z>=0.0)         // half sphere
            {
            a=r0*sin(a)/l;
            }
        else{               // turn hexes above half sphere to cylinder
            z=0.5*pi*r0-l;
            a=r0/l;
            }
        x*=a;
        y*=a;
        hex[i][j][0]=x;
        hex[i][j][1]=y;
        hex[i][j][2]=z;
        }
    }
//---------------------------------------------------------------------------
void hex_draw(int x,int y,GLuint style)     // draw hex x = <0,_gx) , y = <0,_gy)
    {
    y<<=1;
    if ((x&1)==0) y++;
    if ((x<0)||(x+1>=_hx)) return;
    if ((y<0)||(y+2>=_hy)) return;
    glBegin(style);
    glVertex3dv(hex[y+1][x  ]);
    glVertex3dv(hex[y  ][x  ]);
    glVertex3dv(hex[y  ][x+1]);
    glVertex3dv(hex[y+1][x+1]);
    glVertex3dv(hex[y+2][x+1]);
    glVertex3dv(hex[y+2][x  ]);
    glEnd();
    }
//---------------------------------------------------------------------------

И использование:

hexgrid_init(1.5);
hexgrid_half_sphere(1.0);

int x,y;
glColor3f(0.0,0.2,0.3);
for (y=0;y<_gy;y++)
 for (x=0;x<_gx;x++)
  hex_draw(x,y,GL_POLYGON);
glLineWidth(2);
glColor3f(1.0,1.0,1.0);
for (y=0;y<_gy;y++)
 for (x=0;x<_gx;x++)
  hex_draw(x,y,GL_LINE_LOOP);
glLineWidth(1);

И предварительный просмотр:

Для получения дополнительной информации и идей см. Связанные:

• Сделайте сферу с равноотстоящими вершинами
• Превращение цилиндра в сферу без защемления на полюсах