Математика для геодезической сферы
Я пытаюсь создать очень специфическую геодезическую тесселяцию, но я не могу найти в Интернете ничего об этом.
Нормально разделить треугольники икосаэдра на треугольные участки и спроецировать их на сферу. Тем не менее, я заметил анимированный GIF в записи в Википедии для Геодезических куполов, который, похоже, не следует этой схеме. Геодезические сферы обычно содержат смесь в основном гексагональных треугольных пятен с пятиугольными пятнами, образующимися в вершинах исходного икосаэдра; в большинстве случаев эти пятиугольники связаны друг с другом; то есть следование по прямому краю от центра одного пятиугольника приводит к центру другого пятиугольника. Однако в анимации Википедии край от центра одного пятиугольника не пересекает центр соседних пятиугольников; вместо этого он пересекает сторону другого пятиугольника.
Где я могу узнать математику, стоящую за этой конкретной геометрией? В идеале я хотел бы знать алгоритм создания таких тесселяций.
4 ответа
Марсело,
Наиболее часто используемые геодезические тесселяции - это либо класс I, либо класс II. Изображение, на которое вы ссылаетесь, имеет тесселяцию класса III, более конкретно, 4v{3,1}. Классы могут быть построены в виде диаграммы, поэтому:
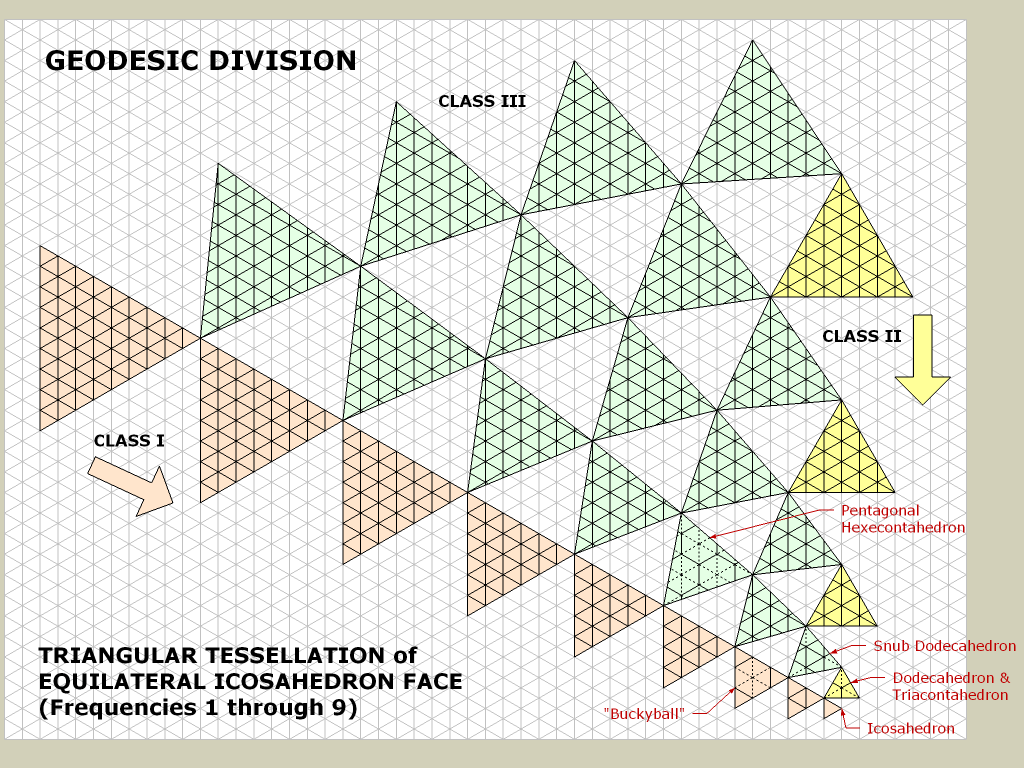
Тесселяции класса III являются киральными и могут иметь поворот левой или правой рукой. Вот зеркальное отображение образца, на который вы ссылались:
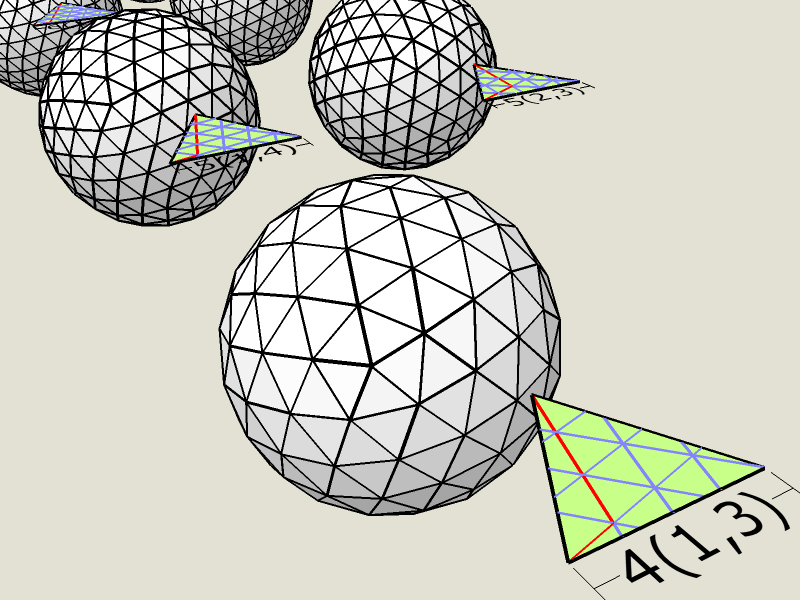
Некоторые 3D-модели сфер класса III можно найти в 3D-моделях Google: http://sketchup.google.com/3dwarehouse/cldetails?mid=b926c2713e303860a99d92cd8fe533cd
Правильная идентификация должна дать вам хорошее начало.
Не стесняйтесь заходить в Группу геодезической помощи; http://groups.google.com/group/GeodesicHelp?hl=en
TaffGoch
Я полагаю, что на самом деле это просто вопрос разрешения (т. Е. Количества подразделений). Тесселяция, которую вы показываете , похоже, исходит из схемы икосаэдра: см. Стр.7 здесь, пример на средней странице. Проверьте остальную часть документа для некоторых деталей вычисления - также его цитируемые ссылки, и некоторые дополнительные примеры кода здесь.
Марсело,
Если вы хотите разработать алгоритмы для генерации любого класса геодезических сфер, вы можете сделать это здесь:
http://thomson.phy.syr.edu/thomsonapplet.htm
Начните с использования опции "custom(m,n)", выберите нужные параметры, затем нажмите кнопку "пауза". Переключитесь на "энергию решетки" и нажмите кнопку "Авто".
Если вы хорошо знакомы с Java, вы можете сохранить файл (ы) "jar" для этого приложения и изучить его содержимое, чтобы выполнить обратную разработку алгоритмов.
Кстати, это Java-приложение также имеет пункт меню "Файл", который может активировать новое окно со списком "Набор точек" (координаты вершины). Я копирую и вставляю их в электронную таблицу Excel, из которой я могу создать "CSV". "файл, который можно впоследствии импортировать в 3D-графические программы.
Taff
