Рисование сферы в OpenGL без использования gluSphere()?
Существуют ли учебники, которые объясняют, как я могу нарисовать сферу в OpenGL, не используя gluSphere()?
Многие учебники по 3D для OpenGL просто на кубах. Я искал, но большинство решений для рисования сферы должны использовать gluSphere(), Есть также сайт, на котором есть код для рисования сферы на этом сайте, но он не объясняет математику рисования сферы. У меня есть и другие версии того, как рисовать сферу в многоугольнике вместо четырехугольников в этой ссылке. Но опять же, я не понимаю, как сферы нарисованы с помощью кода. Я хочу иметь возможность визуализировать, чтобы я мог изменить сферу, если мне нужно.
8 ответов
Один из способов сделать это - начать с платонового тела с треугольными сторонами - например, октаэдра. Затем возьмите каждый треугольник и рекурсивно разбейте его на более мелкие треугольники, например:
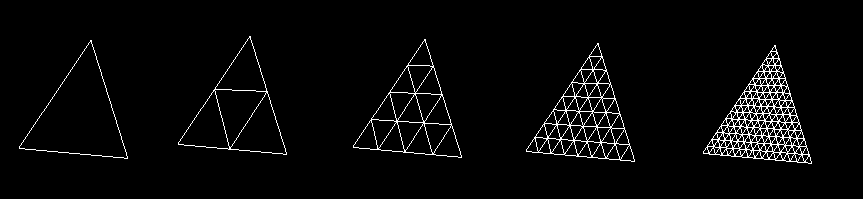
Как только у вас будет достаточное количество точек, вы нормализуете их векторы так, чтобы все они находились на постоянном расстоянии от центра тела. Это приводит к тому, что стороны выпирают в форму, напоминающую сферу, с увеличением плавности по мере увеличения количества точек.
Нормализация здесь означает перемещение точки таким образом, чтобы ее угол относительно другой точки был одинаковым, но расстояние между ними было другим. Вот двухмерный пример.
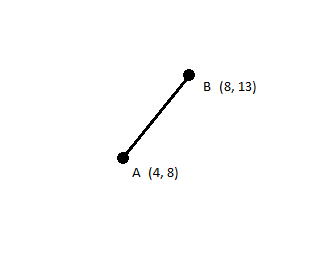
А и В на расстоянии 6 единиц. Но предположим, что мы хотим найти точку на линии AB, которая находится в 12 единицах от A.
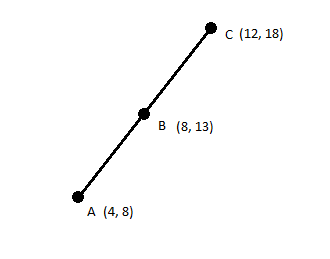
Мы можем сказать, что C является нормализованной формой B относительно A с расстоянием 12. Мы можем получить C с кодом, подобным этому:
#returns a point collinear to A and B, a given distance away from A.
function normalize(a, b, length):
#get the distance between a and b along the x and y axes
dx = b.x - a.x
dy = b.y - a.y
#right now, sqrt(dx^2 + dy^2) = distance(a,b).
#we want to modify them so that sqrt(dx^2 + dy^2) = the given length.
dx = dx * length / distance(a,b)
dy = dy * length / distance(a,b)
point c = new point
c.x = a.x + dx
c.y = a.y + dy
return c
Если мы выполним этот процесс нормализации для множества точек, все относительно одной и той же точки A и с одинаковым расстоянием R, то все нормализованные точки будут лежать на дуге окружности с центром A и радиусом R.
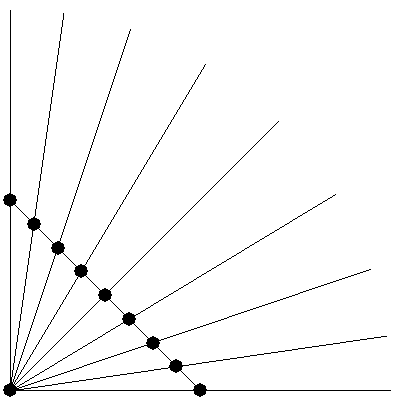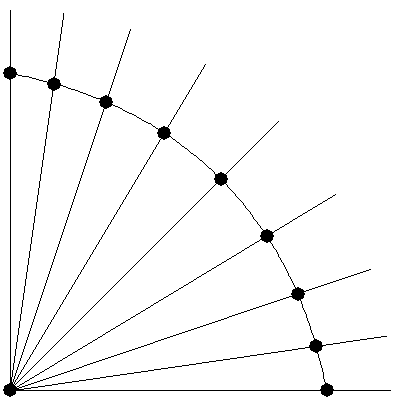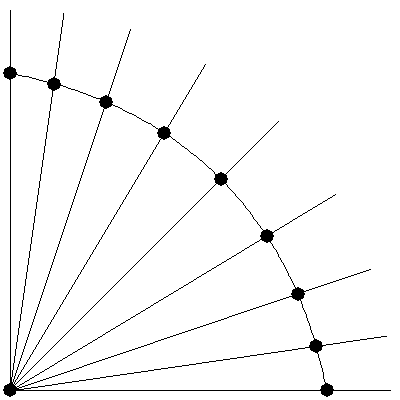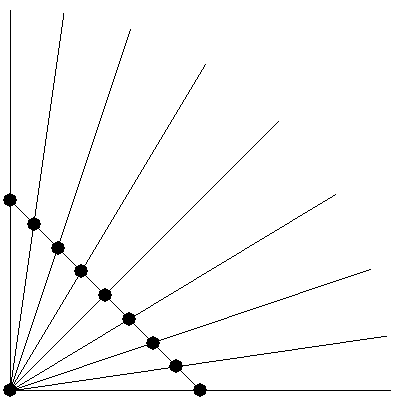
Здесь черные точки начинаются на линии и "выпирают" в дугу.
Этот процесс может быть расширен в три измерения, и в этом случае вы получаете сферу, а не круг. Просто добавьте компонент dz в функцию нормализации.



Если вы посмотрите на сферу в Epcot, вы можете увидеть эту технику в действии. это додекаэдр с выпуклыми гранями, чтобы он выглядел более круглым.
Далее я объясню популярный способ создания сферы с использованием широты и долготы (другой способ, икосферы, уже был объяснен в самом популярном ответе на момент написания этой статьи).
Сфера может быть выражена следующим параметрическим уравнением:
F(u, v) = [cos (u) * sin (v) * r, cos (v) * r, sin (u) * sin (v) * r]
Куда:
- r - радиус;
- u - долгота в диапазоне от 0 до 2π; а также
- v - широта в диапазоне от 0 до π.
Генерация сферы затем включает в себя оценку параметрической функции через фиксированные интервалы.
Например, чтобы сгенерировать 16 линий долготы, вдоль оси u будет 17 линий сетки с шагом π/8 (2π/16) (17-я линия оборачивается вокруг).
Следующий псевдокод генерирует треугольную сетку, оценивая параметрическую функцию через регулярные промежутки времени (это работает для любой параметрической поверхностной функции, а не только для сфер).
В приведенном ниже псевдокоде UResolution - это число точек сетки вдоль оси U (здесь, линии долготы), а VResolution - количество точек сетки вдоль оси V (здесь, линии широты).
var startU=0
var startV=0
var endU=PI*2
var endV=PI
var stepU=(endU-startU)/UResolution // step size between U-points on the grid
var stepV=(endV-startV)/VResolution // step size between V-points on the grid
for(var i=0;i<UResolution;i++){ // U-points
for(var j=0;j<VResolution;j++){ // V-points
var u=i*stepU+startU
var v=j*stepV+startV
var un=(i+1==UResolution) ? EndU : (i+1)*stepU+startU
var vn=(j+1==VResolution) ? EndV : (j+1)*stepV+startV
// Find the four points of the grid
// square by evaluating the parametric
// surface function
var p0=F(u, v)
var p1=F(u, vn)
var p2=F(un, v)
var p3=F(un, vn)
// NOTE: For spheres, the normal is just the normalized
// version of each vertex point; this generally won't be the case for
// other parametric surfaces.
// Output the first triangle of this grid square
triangle(p0, p2, p1)
// Output the other triangle of this grid square
triangle(p3, p1, p2)
}
}
Код в образце объясняется быстро. Вы должны посмотреть на функцию void drawSphere(double r, int lats, int longs), Параметры lat определяет, сколько горизонтальных линий вы хотите иметь в вашей сфере и lon сколько вертикальных линий. r это радиус вашей сферы.
Теперь есть двойная итерация lat/lon и координаты вершины вычисляются с использованием простой тригонометрии.
Рассчитанные вершины теперь отправляются в ваш графический процессор с помощью glVertex...() как GL_QUAD_STRIPЭто означает, что вы отправляете каждые две вершины, которые образуют четырехугольник с двумя ранее отправленными.
Все, что вам нужно понять сейчас, это как работают тригонометрические функции, но я думаю, вы можете легко это понять.
Если вы хотите быть хитрым, как лиса, вы можете сделать полдюйма кода из GLU. Проверьте исходный код MesaGL (http://cgit.freedesktop.org/mesa/mesa/).
void draw_sphere()
{
// z
// |
// __
// /|
// |
// |
// | * \
// | _ _| _ _ _ | _y
// / \c |n / p3 --- p2
// / \o |i | |
// / \s|s z=sin(v) p0 --- p1
// |/__ y=cos(v) *sin(u)
// x=cos(v) *cos(u)
// /
// x
//
double pi = 3.141592;
double di =0.02;
double dj =0.04;
double du =di*2*pi;
double dv =dj*pi;
for (double i = 0; i < 1.0; i+=di) //horizonal
for (double j = 0; j < 1.0; j+=dj) //vertical
{
double u = i*2*pi; //0 to 2pi
double v = (j-0.5)*pi; //-pi/2 to pi/2
double p[][3] = {
cos(v) * cos(u) ,cos(v) * sin(u) ,sin(v),
cos(v) * cos(u + du) ,cos(v) * sin(u + du) ,sin(v),
cos(v + dv)* cos(u + du) ,cos(v + dv)* sin(u + du) ,sin(v + dv),
cos(v + dv)* cos(u) ,cos(v + dv)* sin(u) ,sin(v + dv)};
//normal
glNormal3d(cos(v+dv/2)*cos(u+du/2),cos(v+dv/2)*sin(u+du/2),sin(v+dv/2));
glBegin(GL_POLYGON);
glTexCoord2d(i, j); glVertex3dv(p[0]);
glTexCoord2d(i+di,j); glVertex3dv(p[1]);
glTexCoord2d(i+di,j+dj); glVertex3dv(p[2]);
glTexCoord2d(i, j+dj); glVertex3dv(p[3]);
glEnd();
}
}
См. Красную книгу OpenGL: http://www.glprogramming.com/red/chapter02.html Это решает проблему путем подразделения полигонов.
Мой пример того, как использовать "треугольную полосу" для рисования "полярной" сферы, состоит в рисовании точек попарно:
const float PI = 3.141592f;
GLfloat x, y, z, alpha, beta; // Storage for coordinates and angles
GLfloat radius = 60.0f;
int gradation = 20;
for (alpha = 0.0; alpha < GL_PI; alpha += PI/gradation)
{
glBegin(GL_TRIANGLE_STRIP);
for (beta = 0.0; beta < 2.01*GL_PI; beta += PI/gradation)
{
x = radius*cos(beta)*sin(alpha);
y = radius*sin(beta)*sin(alpha);
z = radius*cos(alpha);
glVertex3f(x, y, z);
x = radius*cos(beta)*sin(alpha + PI/gradation);
y = radius*sin(beta)*sin(alpha + PI/gradation);
z = radius*cos(alpha + PI/gradation);
glVertex3f(x, y, z);
}
glEnd();
}
Первая введенная точка (glVertex3f) является следующим параметрическим уравнением, а вторая смещена на один шаг угла альфа (от следующей параллели).
Адаптация Python ответа @Constantinius:
lats = 10
longs = 10
r = 10
for i in range(lats):
lat0 = pi * (-0.5 + i / lats)
z0 = sin(lat0)
zr0 = cos(lat0)
lat1 = pi * (-0.5 + (i+1) / lats)
z1 = sin(lat1)
zr1 = cos(lat1)
glBegin(GL_QUAD_STRIP)
for j in range(longs+1):
lng = 2 * pi * (j+1) / longs
x = cos(lng)
y = sin(lng)
glNormal(x * zr0, y * zr0, z0)
glVertex(r * x * zr0, r * y * zr0, r * z0)
glNormal(x * zr1, y * zr1, z1)
glVertex(r * x * zr1, r * y * zr1, r * z1)
glEnd()
Хотя принятый ответ решает вопрос, в конце есть небольшое заблуждение. Додекаэдры - это (или могли бы быть) правильные многогранники, где все грани имеют одинаковую площадь. Это похоже на случай с Эпкотом (который, кстати, вообще не является додекаэдром). Поскольку решение, предложенное @Kevin, не обеспечивает эту характеристику, я подумал, что мог бы добавить подход, который делает.
Хороший способ создать многогранник с N-гранью, в котором все вершины лежат в одной сфере и все грани имеют одинаковую площадь / поверхность, начинается с икосаэдра и итеративно подразделяет и нормализует его треугольные грани (как это предлагается в принятом ответе).). Например, додекаэдры - это усеченные икосаэдры.
Правильные икосаэдры имеют 20 граней (12 вершин) и могут быть легко построены из 3 золотых прямоугольников; это просто вопрос наличия этого в качестве отправной точки вместо октаэдра. Вы можете найти пример здесь.
Я знаю, что это немного не по теме, но я верю, что это может помочь, если кто-то придет сюда в поисках этого конкретного случая.
Одним из способов является создание четырехугольника, обращенного к камере, и создание вершинного и фрагментного шейдера, который отображает нечто, похожее на сферу. Вы можете использовать уравнения для круга / сферы, которые вы можете найти в Интернете.
Приятно, что силуэт сферы выглядит одинаково под любым углом. Однако, если сфера находится не в центре перспективного вида, то это может выглядеть скорее как эллипс. Вы можете разработать уравнения для этого и поместить их в затенение фрагмента. Затем, когда игрок движется, необходимо изменить затенение света, если у вас действительно есть игрок, движущийся в трехмерном пространстве вокруг сферы.
Кто-нибудь может прокомментировать, если они попробовали это или это было бы слишком дорого, чтобы быть практичным?