Рассчитать нормали поверхности по глубине изображения, используя соседнее пиксельное произведение
Как видно из заголовка, я хочу вычислить нормали поверхности данного изображения глубины, используя перекрестное произведение соседних пикселей. Я хотел бы использовать Opencv для этого и избегать использования PCL, однако, я не совсем понимаю процедуру, так как мои знания в этой области весьма ограничены. Поэтому я был бы признателен, если бы кто-то мог дать некоторые подсказки. Отметим здесь, что у меня нет никакой другой информации, кроме изображения глубины и соответствующего изображения RGB, поэтому нет K Информация о матрице камеры.
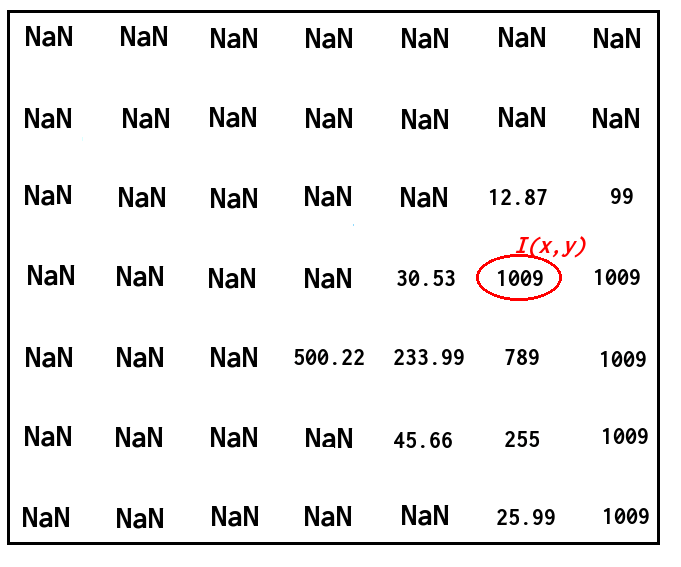
Итак, допустим, что у нас есть следующее изображение глубины:
и я хочу найти вектор нормали в соответствующей точке с соответствующим значением глубины, как на следующем изображении:
Как я могу сделать это, используя перекрестное произведение соседних пикселей? Я не против, если нормы не очень точны.
Благодарю.
Обновить:
Хорошо, я пытался проследить за ответом @ timday и перенести его код на Opencv. Со следующим кодом:
Mat depth = <my_depth_image> of type CV_32FC1
Mat normals(depth.size(), CV_32FC3);
for(int x = 0; x < depth.rows; ++x)
{
for(int y = 0; y < depth.cols; ++y)
{
float dzdx = (depth.at<float>(x+1, y) - depth.at<float>(x-1, y)) / 2.0;
float dzdy = (depth.at<float>(x, y+1) - depth.at<float>(x, y-1)) / 2.0;
Vec3f d(-dzdx, -dzdy, 1.0f);
Vec3f n = normalize(d);
normals.at<Vec3f>(x, y) = n;
}
}
imshow("depth", depth / 255);
imshow("normals", normals);
Я получаю правильный следующий результат (мне пришлось заменить double с float а также Vecd в Vecf, Я не знаю, почему это будет иметь какое-либо значение, хотя)
3 ответа
Вам не нужно использовать перекрестный продукт для этого, но смотрите ниже.
Считайте, что ваш диапазон изображения является функцией z(x,y).
Нормаль к поверхности находится в направлении (-dz/dx,-dz/dy,1). (Где под dz / dx я подразумеваю дифференциал: скорость изменения z с x). И тогда нормали условно нормируются на единицу длины.
Кстати, если вам интересно, откуда это (-dz / dx, -dz / dy, 1)... если вы возьмете 2 ортогональных касательных вектора в плоскости parellel к осям x и y, то это (1,0,dzdx) и (0,1,dzd). Нормаль перпендикулярна касательным, поэтому должно быть (1,0,dzdx)X(0,1,dzdy) - где "X" является перекрестным произведением - то есть (-dzdx,-dzdy,1). Так что ваш кросс-продукт выведен из нормального, но нет необходимости явно вычислять его в коде, когда вы можете просто использовать результирующее выражение для нормали напрямую.
Псевдокод для вычисления нормали единичной длины в точке (x, y) будет выглядеть примерно так:
dzdx=(z(x+1,y)-z(x-1,y))/2.0;
dzdy=(z(x,y+1)-z(x,y-1))/2.0;
direction=(-dxdz,-dydz,1.0)
magnitude=sqrt(direction.x**2 + direction.y**2 + direction.z**2)
normal=direction/magnitude
В зависимости от того, что вы пытаетесь сделать, может иметь смысл заменить значения NaN просто большим числом.
Используя этот подход, из вашего изображения диапазона, я могу получить это:
(Затем я использую обычные направления, рассчитанные для некоторого простого затенения; обратите внимание на "крутой" внешний вид из-за квантования изображения диапазона; в идеале вы должны иметь более высокую точность, чем 8-битные, для данных реального диапазона).
Извините, но не код OpenCV или C++, но только для полноты: полный код, создавший это изображение (GLSL, встроенный в файл Qt QML; может быть запущен с помощью qmlscene Qt5), приведен ниже. Приведенный выше псевдокод можно найти в фрагменте шейдера. main() функция:
import QtQuick 2.2
Image {
source: 'range.png' // The provided image
ShaderEffect {
anchors.fill: parent
blending: false
property real dx: 1.0/parent.width
property real dy: 1.0/parent.height
property variant src: parent
vertexShader: "
uniform highp mat4 qt_Matrix;
attribute highp vec4 qt_Vertex;
attribute highp vec2 qt_MultiTexCoord0;
varying highp vec2 coord;
void main() {
coord=qt_MultiTexCoord0;
gl_Position=qt_Matrix*qt_Vertex;
}"
fragmentShader: "
uniform highp float dx;
uniform highp float dy;
varying highp vec2 coord;
uniform sampler2D src;
void main() {
highp float dzdx=( texture2D(src,coord+vec2(dx,0.0)).x - texture2D(src,coord+vec2(-dx,0.0)).x )/(2.0*dx);
highp float dzdy=( texture2D(src,coord+vec2(0.0,dy)).x - texture2D(src,coord+vec2(0.0,-dy)).x )/(2.0*dy);
highp vec3 d=vec3(-dzdx,-dzdy,1.0);
highp vec3 n=normalize(d);
highp vec3 lightDirection=vec3(1.0,-2.0,3.0);
highp float shading=0.5+0.5*dot(n,normalize(lightDirection));
gl_FragColor=vec4(shading,shading,shading,1.0);
}"
}
}
Есть ли шанс, что вы могли бы предоставить HLSL-версию этого? :D
Код (расчет матрицы) считаю правильным:
def normalization(data):
mo_chang =np.sqrt(np.multiply(data[:,:,0],data[:,:,0])+np.multiply(data[:,:,1],data[:,:,1])+np.multiply(data[:,:,2],data[:,:,2]))
mo_chang = np.dstack((mo_chang,mo_chang,mo_chang))
return data/mo_chang
x,y=np.meshgrid(np.arange(0,width),np.arange(0,height))
x=x.reshape([-1])
y=y.reshape([-1])
xyz=np.vstack((x,y,np.ones_like(x)))
pts_3d=np.dot(np.linalg.inv(K),xyz*img1_depth.reshape([-1]))
pts_3d_world=pts_3d.reshape((3,height,width))
f= pts_3d_world[:,1:height-1,2:width]-pts_3d_world[:,1:height-1,1:width-1]
t= pts_3d_world[:,2:height,1:width-1]-pts_3d_world[:,1:height-1,1:width-1]
normal_map=np.cross(f,l,axisa=0,axisb=0)
normal_map=normalization(normal_map)
normal_map=normal_map*0.5+0.5
alpha = np.full((height-2,width-2,1), (1.), dtype="float32")
normal_map=np.concatenate((normal_map,alpha),axis=2)
Мы должны использовать встроенную функцию камеры под названием "K". Я думаю, что значения f и t основаны на трехмерных точках в координатах камеры.
Для вектора нормали (-1,-1,100) и (255,255,100) имеют один и тот же цвет в 8-битных изображениях, но они совершенно разные в нормальном состоянии. Таким образом, мы должны сопоставить нормальные значения с (0,1) с помощью
normal_map=normal_map*0.5+0.5.
Добро пожаловать в общение.