Создание сторонних сторонников в сетке для 3D-печати
пролог
Это моя попытка повторно задать вопрос закрытым сторонникам Генерации для 3D-печати, поскольку это интересный вопрос, но в нем отсутствуют важные детали... Это задано как вопросы и ответы, и в настоящее время я работаю над кодом для ответа, но не стесняюсь отвечать (я принять лучший ответ).
Описание проблемы
Хорошо, вот некоторая основная информация о проблеме:
Поскольку это огромная проблема, я остановлюсь на общие сетках / поддержке-шаблоне слияния проблемы геометрии.
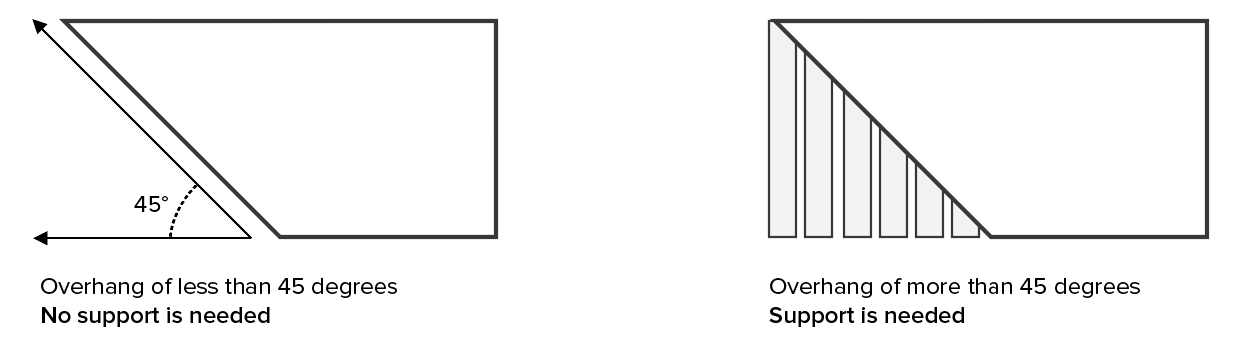
Короче говоря, если мы хотим напечатать любую сетку, мы можем сделать это, только если она соединена с начальной плоскостью до угла ~45 градусов (+/- для различных технологий печати). Поэтому, если у нас есть детали, которые не связаны с этой плоскостью, нам нужно создать мост, который будет удерживать / соединять его с ней. Примерно так (изображение взято со страницы, указанной выше):
Конечно, нам нужно добавить как можно меньшее количество материала, и при этом он должен быть достаточно прочным, чтобы удерживать нашу сетку на месте без изгиба. Кроме того, нам нужно ослабить опору рядом с сеткой, чтобы ее можно было легко разорвать после печати.
Не забывайте, что форма и расположение зависит от многих вещей, таких как материал и технология, используемые тепловые потоки.
Вопрос:
Чтобы сузить эту огромную тему до ответственного вопроса, давайте сосредоточимся исключительно на этой проблеме:
Как объединить трехмерную триангулированную сетку (представление границы как STL) с предопределенным шаблоном поддержки (как 3-сторонняя призма), соединяя его с определенной плоскостью перпендикулярно?
Используя простой C++.
1 ответ
ОК, давайте начнем с абсолютных основ.
форма поддержки
Вы можете использовать любую форму, чтобы соответствовать специфике используемой технологии печати. Самым простым в генерировании в STL является 3-х сторонняя призматическая форма, которая содержит 2 треугольных основания (верх и низ) и 3 стороны, каждая из которых имеет 2 треугольника. Итого 8 треугольников.
Эта форма начнется на некоторой базовой плоскости (
Z=0) и будет идти вверх, пока не достигнет сетки. Однако, чтобы сделать эту работу, поддержка должна иметь небольшойgapмежду сеткой и самим собой, где мы добавим нашу ослабленную структуру соединения с последним сеткой.шаблон поддержки
здесь есть много вариантов, поэтому я выбрал самый простой (но не грязное доказательство), то есть разместить опоры в единой сетке с постоянным расстоянием
gridмежду опорами.поэтому просто наведите луч из каждой позиции сетки на базовой плоскости в направлении вверх и проверьте на пересечение с сеткой. Если найден, поместите опору в это положение с высотой
gapниже точки пересечения.Суставы
Идея состоит в том, чтобы присоединиться к вентилятор очень тонких опор в конусе, как форма соединения и покрытия на подложку поверхности над главной опорной призмой с менее чем 45 градусами угла (так
gapдолжно быть достаточно большим, чтобы покрытьgridрасстояние таким образом).Основная проблема здесь заключается в том, что мы должны подразделить треугольники, к которым мы подключаемся, чтобы мы соответствовали свойствам сетки STL. Чтобы решить проблему соединения (избегать отверстий или нарушения требований к соединению STL), мы можем использовать разные твердые тела для опор и разные для нашей сетки. Это также позволит нам прикасаться к поверхностям без повторной триангуляции, что значительно облегчает эту задачу.
Для простоты я выбрал форму тетраэдра, которую легко построить из треугольников, а также показать слабость соединения сетки / опоры.
Итак, давайте возьмем тестовую сетку STL и поместим ее над нашей базовой плоскостью:
и разместите наши основные опоры:
а также суставы:
Вот код VCL/C++ для этого STL3D.h :
//---------------------------------------------------------------------------
//--- simple STL 3D mesh ----------------------------------------------------
//---------------------------------------------------------------------------
#ifndef _STL3D_h
#define _STL3D_h
//---------------------------------------------------------------------------
#ifdef ComctrlsHPP
TProgressBar *progress=NULL; // loading progress bar for realy big STL files
#endif
void _progress_init(int n);
void _progress (int ix);
void _progress_done();
//---------------------------------------------------------------------------
class STL3D // STL 3D mesh
{
public:
double center[3],size[3],rmax; // bbox center,half sizes, max(size[])
struct _fac
{
float p[3][3]; // triangle vertexes CCW order
float n[3]; // triangle unit normal pointing out
WORD attr;
_fac() {}
_fac(_fac& a) { *this=a; }
~_fac() {}
_fac* operator = (const _fac *a) { *this=*a; return this; }
//_fac* operator = (const _fac &a) { ...copy... return this; }
void compute() // compute normal
{
float a[3],b[3];
vectorf_sub(a,p[1],p[0]);
vectorf_sub(b,p[2],p[1]);
vectorf_mul(n,a,b);
vectorf_one(n,n);
}
double intersect_ray(double *pos,double *dir) // return -1 or distance to triangle and unit ray intersection
{
double p0[3],p1[3],p2[3]; // input triangle vertexes
double e1[3],e2[3],pp[3],qq[3],rr[3]; // dir must be unit vector !!!
double t,u,v,det,idet;
// get points
vector_ld(p0,p[0][0],p[0][1],p[0][2]);
vector_ld(p1,p[1][0],p[1][1],p[1][2]);
vector_ld(p2,p[2][0],p[2][1],p[2][2]);
//compute ray triangle intersection
vector_sub(e1,p1,p0);
vector_sub(e2,p2,p0);
// Calculate planes normal vector
vector_mul(pp,dir,e2);
det=vector_mul(e1,pp);
// Ray is parallel to plane
if (fabs(det)<1e-8) return -1.0;
idet=1.0/det;
vector_sub(rr,pos,p0);
u=vector_mul(rr,pp)*idet;
if ((u<0.0)||(u>1.0)) return -1.0;
vector_mul(qq,rr,e1);
v=vector_mul(dir,qq)*idet;
if ((v<0.0)||(u+v>1.0)) return -1.0;
// distance
t=vector_mul(e2,qq)*idet;
if (t<0.0) t=-1.0;
return t;
}
};
List<_fac> fac; // faces
STL3D() { reset(); }
STL3D(STL3D& a) { *this=a; }
~STL3D() {}
STL3D* operator = (const STL3D *a) { *this=*a; return this; }
//STL3D* operator = (const STL3D &a) { ...copy... return this; }
void reset(){ fac.num=0; compute(); } // clear STL
void draw(); // render STL mesh (OpenGL)
void draw_normals(float size); // render STL normals (OpenGL)
void compute(); // compute bbox
void compute_normals(); // recompute normals from points
void supports(reper &obj); // compute supports with obj placement above base plane z=0
void load(AnsiString name);
void save(AnsiString name);
};
//---------------------------------------------------------------------------
void STL3D::draw()
{
_fac *f; int i,j; BYTE r,g,b;
glBegin(GL_TRIANGLES);
for (f=fac.dat,i=0;i<fac.num;i++,f++)
{
glNormal3fv(f->n);
if (f->attr<32768)
{
r= f->attr &31; r<<=3;
g=(f->attr>> 5)&31; g<<=3;
b=(f->attr>>10)&31; b<<=3;
glColor3ub(r,g,b);
}
for (j=0;j<3;j++) glVertex3fv(f->p[j]);
}
glEnd();
}
//---------------------------------------------------------------------------
void STL3D::draw_normals(float size)
{
_fac *f;
int i; float a[3],b[3];
glBegin(GL_LINES);
for (f=fac.dat,i=0;i<fac.num;i++,f++)
{
vectorf_add(a,f->p[0],f->p[1]);
vectorf_add(a,a ,f->p[2]);
vectorf_mul(a,a,1.0/3.0);
vectorf_mul(b,f->n,size); glVertex3fv(a);
vectorf_add(b,b,a); glVertex3fv(b);
}
glEnd();
}
//---------------------------------------------------------------------------
void STL3D::compute()
{
_fac *f;
int i,j,k;
double p0[3],p1[3];
vector_ld(center,0.0,0.0,0.0);
vector_ld(size,0.0,0.0,0.0);
rmax=0.0;
if (fac.num==0) return;
// bbox
for (k=0;k<3;k++) p0[k]=fac.dat[0].p[0][k];
for (k=0;k<3;k++) p1[k]=fac.dat[0].p[0][k];
for (f=fac.dat,i=0;i<fac.num;i++,f++)
for (j=0;j<3;j++)
for (k=0;k<3;k++)
{
if (p0[k]>f->p[j][k]) p0[k]=f->p[j][k];
if (p1[k]<f->p[j][k]) p1[k]=f->p[j][k];
}
vector_add(center,p0,p1); vector_mul(center,center,0.5);
vector_sub(size ,p1,p0); vector_mul(size ,size ,0.5);
rmax=size[0];
if (rmax<size[1]) rmax=size[1];
if (rmax<size[2]) rmax=size[2];
// attr repair
for (f=fac.dat,i=0;i<fac.num;i++,f++)
if (f->attr==0) f->attr=32768;
}
//---------------------------------------------------------------------------
void STL3D::compute_normals()
{
_fac *f; int i;
for (f=fac.dat,i=0;i<fac.num;i++,f++) f->compute();
}
//---------------------------------------------------------------------------
void STL3D::supports(reper &obj)
{
_fac *f,ff;
int i,j,k;
double p[3],dp[3],x0,y0,h0,x1,y1,x2,y2,h1,t;
// some config values first
const WORD attr0=31<<10; // support attr should be different than joint
const WORD attr1=31<<5; // joint attr should be different than mesh,support
const double grid0=8.0; // distance between supports
const double grid1=2.0; // distance between joints
const double gap=grid0/tan(45.0*deg);// distance between main support and mesh (joint size)
const double ha=1.0; // main support side size
// do not mess with these
const double hx= ha*cos(60.0*deg); // half size of main support in x
const double hy=0.5*ha*sin(60.0*deg); // half size of main support in y
const double grid2=0.4*hy; // distance between joints bases
const double ga=2.0*grid2*grid1/grid0; // main support side size
const double gx=hx*grid2/grid0; // half size of joint support in x
const double gy=hy*grid2/grid0; // half size of joint support in y
// apply placement obj (may lose some accuracy) not needed if matrices are not used
for (f=fac.dat,i=0;i<fac.num;i++,f++)
{
for (j=0;j<3;j++)
{
for (k=0;k<3;k++) p[k]=f->p[j][k]; // float->double
obj.l2g(p,p);
for (k=0;k<3;k++) f->p[j][k]=p[k]; // double->float
}
for (k=0;k<3;k++) p[k]=f->n[k]; // float->double
obj.l2g_dir(p,p);
for (k=0;k<3;k++) f->n[k]=p[k]; // double->float
} compute();
// create supports
for (x0=center[0]-size[0]+(0.5*grid0);x0<=center[0]+size[0]-(0.5*grid0);x0+=grid0)
for (y0=center[1]-size[1]+(0.5*grid0);y0<=center[1]+size[1]-(0.5*grid0);y0+=grid0)
{
// cast ray x0,y0,0 in Z+ direction to check for mesh intersection to compute the support height h0
h0=center[2]+size[2]+1e6;
vector_ld(p,x0,y0,0.0);
vector_ld(dp,0.0,0.0,+1.0);
for (f=fac.dat,i=0;i<fac.num;i++,f++)
{
t=f->intersect_ray(p,dp);
if ((t>=0.0)&&(t<h0)) h0=t;
}
if (h0>center[2]+size[2]+1e5) continue; // skip non intersected rays
h0-=gap; if (h0<0.0) h0=0.0;
// main suport prism
ff.attr=attr0;
// sides
ff.attr=attr0;
vectorf_ld(ff.p[0],x0-hx,y0-hy,0.0);
vectorf_ld(ff.p[1],x0+hx,y0-hy,0.0);
vectorf_ld(ff.p[2],x0-hx,y0-hy, h0); ff.compute(); fac.add(ff);
vectorf_ld(ff.p[0],x0+hx,y0-hy,0.0);
vectorf_ld(ff.p[1],x0+hx,y0-hy, h0);
vectorf_ld(ff.p[2],x0-hx,y0-hy, h0); ff.compute(); fac.add(ff);
vectorf_ld(ff.p[0],x0-hx,y0-hy, h0);
vectorf_ld(ff.p[1],x0 ,y0+hy,0.0);
vectorf_ld(ff.p[2],x0-hx,y0-hy,0.0); ff.compute(); fac.add(ff);
vectorf_ld(ff.p[0],x0-hx,y0-hy, h0);
vectorf_ld(ff.p[1],x0 ,y0+hy, h0);
vectorf_ld(ff.p[2],x0 ,y0+hy,0.0); ff.compute(); fac.add(ff);
vectorf_ld(ff.p[0],x0 ,y0+hy, h0);
vectorf_ld(ff.p[1],x0+hx,y0-hy,0.0);
vectorf_ld(ff.p[2],x0 ,y0+hy,0.0); ff.compute(); fac.add(ff);
vectorf_ld(ff.p[0],x0 ,y0+hy, h0);
vectorf_ld(ff.p[1],x0+hx,y0-hy, h0);
vectorf_ld(ff.p[2],x0+hx,y0-hy,0.0); ff.compute(); fac.add(ff);
// base triangles
vectorf_ld(ff.p[0],x0 ,y0+hy,0.0);
vectorf_ld(ff.p[1],x0+hx,y0-hy,0.0);
vectorf_ld(ff.p[2],x0-hx,y0-hy,0.0); ff.compute(); fac.add(ff);
vectorf_ld(ff.p[0],x0-hx,y0-hy, h0);
vectorf_ld(ff.p[1],x0+hx,y0-hy, h0);
vectorf_ld(ff.p[2],x0 ,y0+hy, h0); ff.compute(); fac.add(ff);
// joints
for (x1=x0-(0.5*grid0),x2=x0-(0.5*grid2);x1<=x0+(0.5*grid0);x1+=grid1,x2+=ga)
for (y1=y0-(0.5*grid0),y2=y0-(1.9*grid2);y1<=y0+(0.5*grid0);y1+=grid1,y2+=ga)
{
// cast ray x1,y1,0 in Z+ direction to check for mesh intersection to compute the joint height h1
h1=h0+gap+1e6;
vector_ld(p,x1,y1,0.0);
vector_ld(dp,0.0,0.0,+1.0);
for (f=fac.dat,i=0;i<fac.num;i++,f++)
{
t=f->intersect_ray(p,dp);
if ((t>=0.0)&&(t<h1)) h1=t;
}
if (h1>h0+gap+1e5) continue; // skip non intersected rays
// tetrahedron joints
ff.attr=attr1;
// base triangle
vectorf_ld(ff.p[0],x2 ,y2+gy,h0);
vectorf_ld(ff.p[1],x2+gx,y2-gy,h0);
vectorf_ld(ff.p[2],x2-gx,y2-gy,h0); ff.compute(); fac.add(ff);
// sides
vectorf_ld(ff.p[0],x2+gx,y2-gy,h0);
vectorf_ld(ff.p[1],x2 ,y2+gy,h0);
vectorf_ld(ff.p[2],x1 ,y1 ,h1); ff.compute(); fac.add(ff);
vectorf_ld(ff.p[0],x2 ,y2+gy,h0);
vectorf_ld(ff.p[1],x2-gx,y2-gy,h0);
vectorf_ld(ff.p[2],x1 ,y1 ,h1); ff.compute(); fac.add(ff);
vectorf_ld(ff.p[0],x2+gx,y2+gy,h0);
vectorf_ld(ff.p[1],x2-gx,y2-gy,h0);
vectorf_ld(ff.p[2],x1 ,y1 ,h1); ff.compute(); fac.add(ff);
}
}
// reverse placement obj (may lose some accuracy) not needed if matrices are not used
for (f=fac.dat,i=0;i<fac.num;i++,f++)
{
for (j=0;j<3;j++)
{
for (k=0;k<3;k++) p[k]=f->p[j][k]; // float->double
obj.g2l(p,p);
for (k=0;k<3;k++) f->p[j][k]=p[k]; // double->float
}
for (k=0;k<3;k++) p[k]=f->n[k]; // float->double
obj.g2l_dir(p,p);
for (k=0;k<3;k++) f->n[k]=p[k]; // double->float
} compute();
}
//---------------------------------------------------------------------------
void STL3D::load(AnsiString name)
{
int adr,siz,hnd;
BYTE *dat;
AnsiString lin,s;
int i,j,l,n;
_fac f;
reset(); f.attr=0;
siz=0;
hnd=FileOpen(name,fmOpenRead);
if (hnd<0) return;
siz=FileSeek(hnd,0,2);
FileSeek(hnd,0,0);
dat=new BYTE[siz];
if (dat==NULL) { FileClose(hnd); return; }
FileRead(hnd,dat,siz);
FileClose(hnd);
adr=0; s=txt_load_str(dat,siz,adr,true);
// ASCII
if (s=="solid")
{
_progress_init(siz); int progress_cnt=0;
for (adr=0;adr<siz;)
{
progress_cnt++; if (progress_cnt>=128) { progress_cnt=0; _progress(adr); }
lin=txt_load_lin(dat,siz,adr,true);
for (i=1,l=lin.Length();i<=l;)
{
s=str_load_str(lin,i,true);
if (s=="solid") { name=str_load_str(lin,i,true); break; }
if (s=="endsolid") break;
if (s=="facet")
{
j=0;
s=str_load_str(lin,i,true);
f.n[0]=str2num(str_load_str(lin,i,true));
f.n[1]=str2num(str_load_str(lin,i,true));
f.n[2]=str2num(str_load_str(lin,i,true));
}
if (s=="vertex")
if (j<3)
{
f.p[j][0]=str2num(str_load_str(lin,i,true));
f.p[j][1]=str2num(str_load_str(lin,i,true));
f.p[j][2]=str2num(str_load_str(lin,i,true));
j++;
if (j==3) fac.add(f);
}
break;
}
}
}
// binary
else{
adr=80;
n=((DWORD*)(dat+adr))[0]; adr+=4;
fac.allocate(n); fac.num=0;
_progress_init(n); int progress_cnt=0;
for (i=0;i<n;i++)
{
if (adr+50>siz) break; // error
progress_cnt++; if (progress_cnt>=128) { progress_cnt=0; _progress(i); }
f.n[0]=((float*)(dat+adr))[0]; adr+=4;
f.n[1]=((float*)(dat+adr))[0]; adr+=4;
f.n[2]=((float*)(dat+adr))[0]; adr+=4;
for (j=0;j<3;j++)
{
f.p[j][0]=((float*)(dat+adr))[0]; adr+=4;
f.p[j][1]=((float*)(dat+adr))[0]; adr+=4;
f.p[j][2]=((float*)(dat+adr))[0]; adr+=4;
}
f.attr=((WORD*)(dat+adr))[0]; adr+=2; // attributes
fac.add(f);
}
}
_progress_done();
delete[] dat;
compute();
}
//---------------------------------------------------------------------------
void STL3D::save(AnsiString name)
{
// ToDo
}
//---------------------------------------------------------------------------
void _progress_init(int n)
{
#ifdef ComctrlsHPP
if (progress==NULL) return;
progress->Position=0;
progress->Max=n;
progress->Visible=true;
#endif
}
//---------------------------------------------------------------------------
void _progress (int ix)
{
#ifdef ComctrlsHPP
if (progress==NULL) return;
progress->Position=ix;
progress->Update();
#endif
}
//---------------------------------------------------------------------------
void _progress_done()
{
#ifdef ComctrlsHPP
if (progress==NULL) return;
progress->Visible=false;
#endif
}
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------
Использование простое:
#include "STL3D.h" // STL mesh (this is the important stuff)
STL3D mesh; // point cloud and tetrahedronal mesh
mesh.load("space_invader_magnet.stl");
mesh.supports(obj); // obj is object holding 4x4 uniform matrix of placement if you STL is already placed than it is not needed
Я использовал много вещей из моего движка OpenGL, как динамический List<> шаблон:
List<double> xxx; такой же как double xxx[];xxx.add(5); добавляет 5 в конец списка xxx[7] элемент массива доступа (безопасный) xxx.dat[7] доступ к элементу массива (небезопасный, но быстрый прямой доступ) xxx.num фактический используемый размер массива xxx.reset() очищает массив и устанавливает xxx.num=0xxx.allocate(100) предварительно выделить место для 100 Предметы
или векторная и матричная математика (vectorf_ работает с float* а также vector_ с double) что не так уж важно. Если вам нужна математика, посмотрите:
Если STL уже размещен (без матрицы), то ни преобразования размещения, ни obj нужен вообще. Код отражает пули выше. Я хотел сделать это как можно проще, поэтому никаких оптимизаций пока нет.
gap а также grid Константы жестко закодированы в функции поддержки и еще не установлены в допустимые значения.
[Заметки]
Теперь это едва покрывает только самую основную проблему, и есть много крайних случаев, оставленных необработанными, чтобы держать это "коротким". Сам код не проверяет, находятся ли треугольники выше наклона 45 градусов, но это можно сделать с помощью простой проверки нормального угла, например:
if (acos(dot(normal,(0.0,0.0,1.0))<45.0*deg) continue;
Также необходимо добавить опоры между частями сетки, например, если ваш объект имеет больше слоев, чем будет поддерживаться только первый слой из базовой плоскости. остальные должны использовать слой под собой... и использовать ослабленные соединения с обеих сторон поддержки. Это аналогично размещению первого слоя опор, который вам просто необходим для наведения луча в обоих направлениях... или наложения непрерывного луча, проходящего через весь bbox, и проверки начала / конца поверхностей путем анализа нормального направления на луч (простой знак точки товар). Например, для размещения сетки это может понадобиться (для некоторых технологий):
При проектировании подставок необходимо учитывать правильное правило намотки (CCW) и нормальное направление (выход) для процесса печати...