Растяжение проблемы с помощью пользовательской матрицы просмотра

Question

В настоящее время я работаю над своей собственной библиотекой 2D Maths для моего проекта, чтобы улучшить мое понимание математики базовой матрицы. В прошлом я использовал библиотеки, такие как GLM, но я чувствовал, что это может быть полезным для изучения.

Большая часть этого была проста, и большинство моих классов по математике интегрируются и хорошо работают с OpenGL, однако моя матрица представления, кажется, растягивает мой квад по краям окна.

Обратите внимание, что это не проблема перспективы, я не только использую Ортографическую Матрицу, но я отделил это от MVP, использую матрицу представления вместо MVP, и проблема все еще сохраняется.

Ниже приведен мой код создания матрицы просмотра:

Matrix4x4 GenerateView(const Vector2f &cameraPosition)
{
    Matrix4x4 mat;

    //Right
    mat.elements[0][0] = 1;
    mat.elements[0][1] = 0;
    mat.elements[0][2] = 0;
    mat.elements[0][3] = -Dot(cameraPosition.x, cameraPosition.y, 10, 1, 0, 0);

    //Up
    mat.elements[1][0] = 0;
    mat.elements[1][1] = 1;
    mat.elements[1][2] = 0;
    mat.elements[1][3] = -Dot(cameraPosition.x, cameraPosition.y, 10, 0, 1, 0);

    //Look
    mat.elements[2][0] = cameraPosition.x;
    mat.elements[2][1] = cameraPosition.y;
    mat.elements[2][2] = -1;
    mat.elements[2][3] = -Dot(cameraPosition.x, cameraPosition.y, 10, cameraPosition.x, cameraPosition.y, -1);

    //Last Column
    mat.elements[3][0] = 0;
    mat.elements[3][1] = 0;
    mat.elements[3][2] = 0;
    mat.elements[3][3] = 1;
    return mat;
}

Матрицы являются основными столбца (если я правильно понимаю). Мне было неясно, относится ли "взгляд" к переднему вектору, поэтому я попробовал это так же, как "центр", но проблема сохраняется.

//Look
    mat.elements[2][0] = 0;
    mat.elements[2][1] = 0;
    mat.elements[2][2] = -1;
    mat.elements[2][3] = -Dot(cameraPosition.x, cameraPosition.y, 10, 0, 0, -1);

Наконец, если кто-то подозревает, что продукт Dot реализован неправильно:

float Dot(float x1, float y1, float z1, float x2, float y2, float z2)
{
    return x1 * x2 + y1 * y2 + z1 * z2;
}

Answer 1

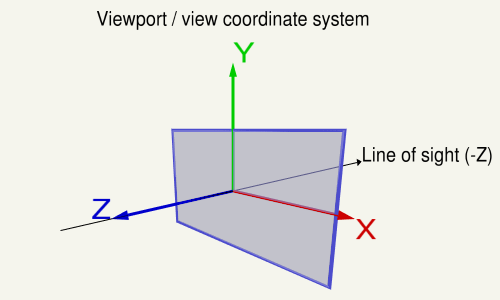
В области просмотра ось X направлена ​​влево, ось Y вверх и ось Z вне вида (обратите внимание, что в правой системе ось Z является перекрестным произведением оси X и оси Y). Ось).

Обратите внимание, что матрица преобразования обычно выглядит так:

( X-axis.x, X-axis.y, X-axis.z, 0 )
( Y-axis.x, Y-axis.y, Y-axis.z, 0 )
( Z-axis.x, Z-axis.y, Z-axis.z, 0 )
( trans.x,  trans.y,  trans.z,  1 )

Код ниже определяет матрицу, которая точно инкапсулирует шаги, необходимые для вычисления взгляда на сцену:

• Преобразование координат модели в координаты области просмотра.
• Вращение, чтобы смотреть в направлении взгляда.
• Движение в положение глаз

Matrix4x4 LookAt( const Vector3f &pos, const Vector3f &target, const Vector3f &up )
{ 
    Vector3f mz( pos[0] - target[0], pos[1] - target[1], pos[2] - target[2] };
    Normalize( mz );
    Vector3f my( up[0], up[1], up[2] );
    Vector3f mx = Cross( my, mz );
    Normalize( mx );
    my = Cross( mz, mx );

    Matrix4x4 m;
    m.elements[0][0] = mx[0]; m.elements[0][1] = my[0]; m.elements[0][2] = mz[0]; m.elements[0][3] = 0.0f;
    m.elements[1][0] = mx[1]; m.elements[1][1] = my[1]; m.elements[1][2] = mz[1]; m.elements[1][3] = 0.0f;
    m.elements[2][0] = mx[2]; m.elements[2][1] = my[2]; m.elements[2][2] = mz[2]; m.elements[2][3] = 0.0f;

    m.elements[3][0] = Dot(mx, pos);
    m.elements[3][1] = Dot(my, pos);
    m.elements[3][2] = Dot(Vector3f(-mz[0], -mz[1], -mz[2]), pos);
    m.elements[3][3] = 1.0f;

    return m;
}

Vector3f Cross( const Vector3f &a, const Vector3f &b )
{ 
    return Vector3f( a[1] * b[2] - a[2] * b[1], a[2] * b[0] - a[0] * b[2], a[0] * b[1] - a[1] * b[0] ); 
}

float Dot( const Vector3f &a, const Vector3f &b )
{ 
    return a[0]*b[0] + a[1]*b[1] + a[2]*b[2];
}

void Normalize( Vector3f &v )
{ 
    float len = sqrt( v[0] * v[0] + v[1] * v[1] + v[2] * v[2] );
    v = Vector3f( v[0] / len, v[1] / len, v[2] / len );
}