Логистическая регрессия возвращает ошибку, но работает нормально на сокращенном наборе данных
Я был бы признателен за ваш вклад в этом много!
Я работаю над логистической регрессией, но по какой-то причине она не работает:
mod1<-glm(survive~reLDM2+yr+yr2+reLDM2:yr +reLDM2:yr2+NestAge0,
family=binomial(link=logexp(NSSH1$exposure)),
data=NSSH1, control = list(maxit = 50))
Когда я запускаю ту же модель с меньшим количеством данных, это работает! Но с полным набором данных я получаю сообщения об ошибках и предупреждения:
Error: inner loop 1; cannot correct step size
In addition: Warning messages:
1: step size truncated due to divergence
2: step size truncated due to divergence
Это данные: https://www.dropbox.com/s/8ib8m1fh176556h/NSSH1.csv?dl=0
Зарегистрируйте функцию связи с экспозицией из пользовательской функции связи для glmer для моделирования выживания с известной судьбой:
library(MASS)
logexp <- function(exposure = 1) {
linkfun <- function(mu) qlogis(mu^(1/exposure))
## FIXME: is there some trick we can play here to allow
## evaluation in the context of the 'data' argument?
linkinv <- function(eta) plogis(eta)^exposure
mu.eta <- function(eta) exposure * plogis(eta)^(exposure-1) *
.Call(stats:::C_logit_mu_eta, eta, PACKAGE = "stats")
valideta <- function(eta) TRUE
link <- paste("logexp(", deparse(substitute(exposure)), ")",
sep="")
structure(list(linkfun = linkfun, linkinv = linkinv,
mu.eta = mu.eta, valideta = valideta,
name = link),
class = "link-glm")
}
1 ответ
TL; д-р вы попали в беду, потому что ваш yr а также yr2 предикторы (предположительно год и год в квадрате) в сочетании с необычной функцией связи вызывают численные проблемы; Вы можете обойти это, используя пакет glm2, но я бы, по крайней мере, немного подумал о том, имеет ли смысл в этом случае подходить к квадратному году.
Обновление: метод грубой силы с mle2 началось ниже; еще не написал это, чтобы сделать полную модель с взаимодействиями.
Народная теорема Эндрю Гельмана, вероятно, применима и здесь:
Если у вас есть вычислительные проблемы, часто есть проблема с вашей моделью.
Я начал с упрощенной версии вашей модели, без взаимодействия...
NSSH1 <- read.csv("NSSH1.csv")
source("logexpfun.R") ## for logexp link
mod1 <- glm(survive~reLDM2+yr+yr2+NestAge0,
family=binomial(link=logexp(NSSH1$exposure)),
data=NSSH1, control = list(maxit = 50))
... который отлично работает Теперь давайте попробуем увидеть, в чем проблема:
mod2 <- update(mod1,.~.+reLDM2:yr) ## OK
mod3 <- update(mod1,.~.+reLDM2:yr2) ## OK
mod4 <- update(mod1,.~.+reLDM2:yr2+reLDM2:yr) ## bad
Итак, у нас проблемы с одновременным включением обоих взаимодействий. Как эти предикторы на самом деле связаны друг с другом? Посмотрим...
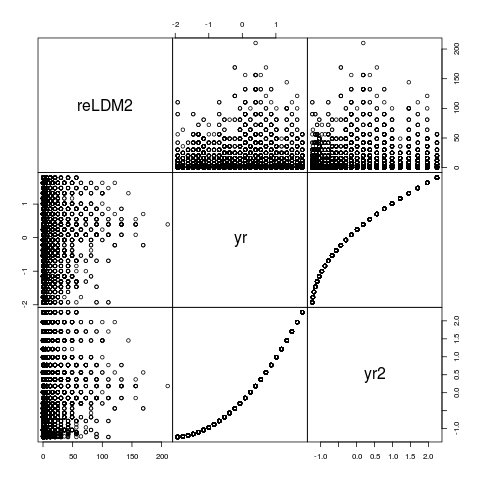
pairs(NSSH1[,c("reLDM2","yr","yr2")],gap=0)
yr а также yr2 не идеально коррелированы, но они идеально коррелируют по рангу, и, конечно, неудивительно, что они взаимно обновляются друг с другом. Обновление: конечно, год и квадрат год выглядят так! даже используя poly(yr,2) , который создает ортогональный многочлен, в этом случае не помогает... тем не менее, стоит посмотреть на параметры в случае, если он дает подсказку...
Как уже упоминалось выше, мы можем попробовать glm2 (вставная замена для glm с более надежным алгоритмом) и посмотрим, что произойдет...
library(glm2)
mod5 <- glm2(survive~reLDM2+yr+yr2+reLDM2:yr +reLDM2:yr2+NestAge0,
family=binomial(link=logexp(NSSH1$exposure)),
data=NSSH1, control = list(maxit = 50))
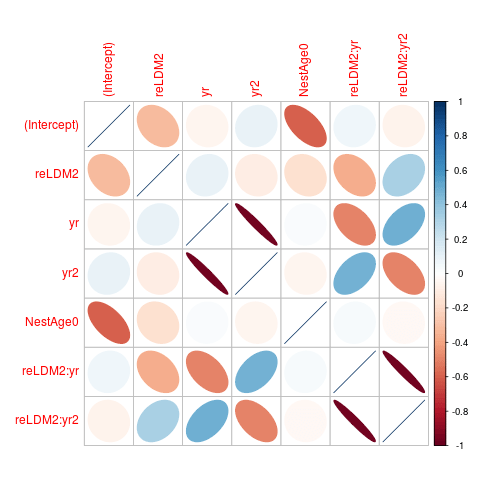
Теперь мы получаем ответ. Если мы проверим cov2cor(vcov(mod5)) мы видим, что yr а также yr2 параметры (и параметры для их взаимодействия с reLDM2 сильно отрицательно коррелированы (около -0,97). Давайте представим, что...
library(corrplot)
corrplot(cov2cor(vcov(mod5)),method="ellipse")
Что если мы попытаемся сделать это грубой силой?
library(bbmle)
link <- logexp(NSSH1$exposure)
fit <- mle2(survive~dbinom(prob=link$linkinv(eta),size=1),
parameters=list(eta~reLDM2+yr+yr2+NestAge0),
start=list(eta=0),
data=NSSH1,
method="Nelder-Mead") ## more robust than default BFGS
summary(fit)
## Estimate Std. Error z value Pr(z)
## eta.(Intercept) 4.3627816 0.0402640 108.3545 < 2e-16 ***
## eta.reLDM2 -0.0019682 0.0011738 -1.6767 0.09359 .
## eta.yr -6.0852108 0.2068159 -29.4233 < 2e-16 ***
## eta.yr2 5.7332780 0.1950289 29.3971 < 2e-16 ***
## eta.NestAge0 0.0612248 0.0051272 11.9411 < 2e-16 ***
Это кажется разумным (вы должны проверить прогнозируемые значения и убедиться, что они имеют смысл...), но...
cc <- confint(fit) ## "profiling has found a better solution"
Это возвращает mle2 объект, но один с искаженным слотом вызова, так что это неприятно печатать результаты.
coef(cc)
## eta.(Intercept) eta.reLDM2
## 4.329824508 -0.011996582
## eta.yr eta.yr2
## 0.101221970 0.093377127
## eta.NestAge0
## 0.003460453
##
vcov(cc) ## all NA values! problem?
Попробуйте перезапустить эти возвращенные значения...
fit2 <- update(fit,start=list(eta=unname(coef(cc))))
coef(summary(fit2))
## Estimate Std. Error z value Pr(z)
## eta.(Intercept) 4.452345889 0.033864818 131.474082 0.000000e+00
## eta.reLDM2 -0.013246977 0.001076194 -12.309102 8.091828e-35
## eta.yr 0.103013607 0.094643420 1.088439 2.764013e-01
## eta.yr2 0.109709373 0.098109924 1.118229 2.634692e-01
## eta.NestAge0 -0.006428657 0.004519983 -1.422274 1.549466e-01
Теперь мы можем получить доверительные интервалы...
ci2 <- confint(fit2)
## 2.5 % 97.5 %
## eta.(Intercept) 4.38644052 4.519116156
## eta.reLDM2 -0.01531437 -0.011092655
## eta.yr -0.08477933 0.286279919
## eta.yr2 -0.08041548 0.304251382
## eta.NestAge0 -0.01522353 0.002496006
Кажется, это работает, но я бы очень подозрительно относился к этим припадкам. Возможно, вам следует попробовать другие оптимизаторы, чтобы убедиться, что вы можете вернуться к тем же результатам. Может быть хорошей идеей является лучший инструмент оптимизации, такой как AD Model Builder или Template Model Builder.
Я не придерживаюсь бездумно отбрасывающих предикторов с сильно коррелированными оценками параметров, но это может быть разумным временем для его рассмотрения.