Эффективное размещение 2D-фигур в прямоугольнике. Как подойти к этому?
Я искал все семь интернетов, но безрезультатно. Кажется, ближе всего к тому, что мне нужно, это проблема режущего материала, только в 2D (что вызывает разочарование, поскольку Википедия не дает никаких указаний о том, как ее решить). Еще одна похожая проблема - разворачивание ультрафиолета. Там есть решения, но только те, которые вы получаете из надстроек различных 3D-программ.
Коротко говоря, я хочу вот что: учитывая прямоугольник с известной шириной и высотой, я должен выяснить, сколько фигур (многоугольников) известных размеров (которые могут быть повернуты по желанию) я могу уместить внутри этого прямоугольника.
Например, я мог бы выбрать Т-образную фигуру и в одном и том же прямоугольнике я мог бы упаковать ее обе эффективно, в результате получилось 4 фигуры на прямоугольник

а также мозаику их на основе их ограничивающих рамок, случай, в котором я мог поместиться только 3
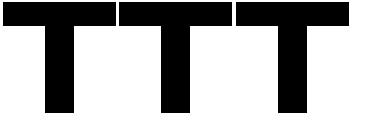
Но, конечно, это только пример... и я не думаю, что это было бы полезно для решения этого конкретного случая. Единственные подходы, о которых я могу думать прямо сейчас, - это либо отступление по своей сложности, либо решение только частных случаев этой проблемы. Итак... есть идеи?
2 ответа
Кто-нибудь хочет поиграть в тетрис (часть вашей проблемы)?
Это известно как проблема упаковки. Не зная, с какими формами вы, вероятно, столкнетесь раньше времени, может быть очень трудно, если не невозможно, придумать алгоритм, который даст вам лучший ответ. Скорее всего, если ваши полигоны не являются "хорошими" полигонами (кругами, квадратами, равносторонними треугольниками и т. Д.), Вам, вероятно, придется согласиться на эвристику, которая большую часть времени дает вам примерное наилучшее решение.
Одна общая эвристика (хотя далеко не оптимальная в зависимости от формы входного многоугольника) состоит в том, чтобы упростить задачу, нарисовав прямоугольник вокруг многоугольника так, чтобы прямоугольник был достаточно большим, чтобы покрыть многоугольник. (В качестве примера на диаграмме ниже мы рисуем красный прямоугольник вокруг синего многоугольника.)
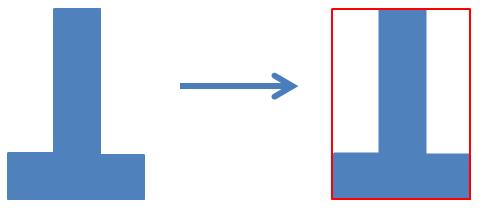
Как только мы это сделаем, мы сможем взять этот прямоугольник и попытаться разместить как можно больше этого прямоугольника в большом прямоугольнике. Это упрощает проблему в проблему упаковки прямоугольника, которую легче решить и обернуть вокруг. Пример алгоритма для этого находится по следующей ссылке:
Эффективный подход к рекурсивному разбиению для упаковки одинаковых прямоугольников в прямоугольник.
Очевидно, что эта эвристика не оптимальна, когда рассматриваемый многоугольник не похож на форму прямоугольника, но дает минимальную базовую линию для работы, особенно если у вас мало знаний о том, как будет выглядеть ваш многоугольник. как (или есть большая разница в том, как будет выглядеть многоугольник). Используя этот алгоритм, он заполнил бы большой прямоугольник так:
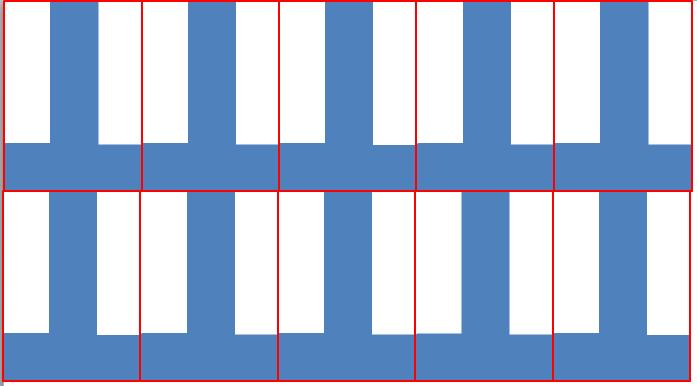
Вот то же изображение без промежуточных прямоугольников:

В случае этих Т-образных многоугольников эвристика не является наилучшей, какой она могла бы быть (на самом деле это может быть почти наихудший сценарий для этого предложенного приближения), но она будет очень хорошо работать для других типов многоугольников.
Подумайте, что сказал другой ответ, поместив буквы t в квадрат, но вместо того, чтобы просто оставить его в виде квадрата, задайте фигуры в списке. Затем используйте True и False, чтобы заполнить вложенный список как фигуру, т.е. [[True,True,True],[False,True,False]] для вашей T-формы. Затем используйте функцию для размещения фигур на сетке. Чтобы оптимизировать результаты, создайте трекер, который будет обращать внимание на то, сколько ложных значений в новой фигуре перекрываются с истинными значениями, которые уже есть в сетке из предыдущих фигур. Функция поместит фигуру в место с наибольшим количеством наложений. Должны быть изменения, чтобы создавать все более и более оптимизацию, но это общая предпосылка, которую вы ищете.