Координаты одинаково удаленных n точек на окружности в R?

Я хочу получить координаты одинаково удаленных n точек на окружности в R.

Математически решение: exp((2*pi * i)*(k/n)), где 0 <= k

Есть много вопросов SOF для решения этой проблемы. Все решения не в среде R:

Равномерное распределение n точек на сфере (представлены решения java, python)

Генерация точек на окружности (решение без R)

вычислить координаты пикселей для 8 равноотстоящих точек на окружности (решение Python)

рисование точек, равномерно распределенных по кругу (решение без R)

Как построить точки вокруг круга в R (нет одинакового расстояния)

Координаты каждой точки на окружности окружности (решение без R)

Координаты точек, разделяющих окружность на n равных половин в Pebble

Как эффективно нарисовать ровно N точек на экране? (решение Python)

Приблизительное положение на окружности для n точек (не R решение)

Определение векторных точек на окружности

Что я сделал для решения:

# For 4 points, 0<=k<4    
exp((2*pi*sqrt(-1))*(0/4)); exp((2*pi*sqrt(-1))*(1/4)); exp((2*pi*sqrt(-1))*(2/4)); exp((2*pi*sqrt(-1))*(3/4))

Комплексное число i не определено в R. Не существует такой константы, как противоположность pi (3.14). Уловка sqrt(-1), чтобы подобрать меня, не работает; Ошибка:

[1] NaN 
Warning message: In sqrt(-1) : NaNs produced
Источник

3 ответа

Решение

Йо тоже может попробовать это (и избежать сложной арифметики), чтобы иметь точки на окружности юнитов на реальной плоскости:

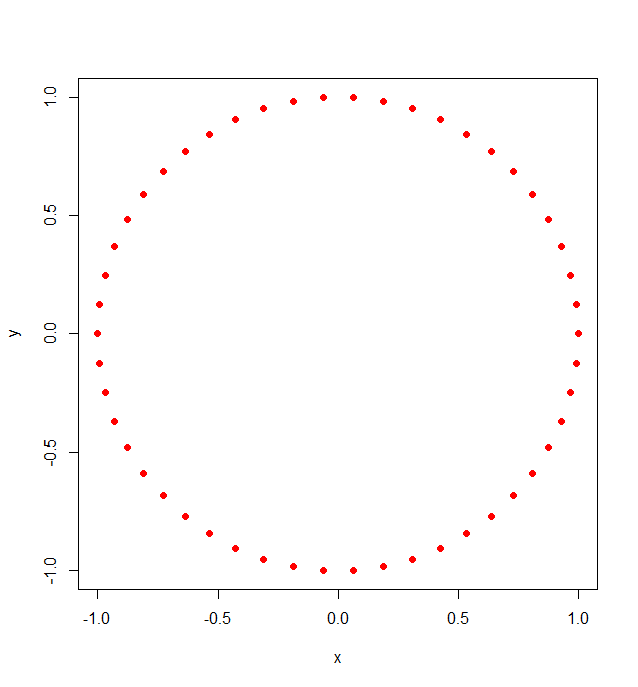
n <- 50 # number of points you want on the unit circle
pts.circle <- t(sapply(1:n,function(r)c(cos(2*r*pi/n),sin(2*r*pi/n))))
plot(pts.circle, col='red', pch=19, xlab='x', ylab='y')

введите описание изображения здесь

Источник

Мы можем использовать комплексные числа для достижения этого довольно просто, но вам нужно использовать правильный синтаксис. в общем, комплексные числа могут быть записаны как ai + b (например 3i + 2). Если есть только мнимый компонент, мы можем написать просто ai, Итак, воображаемый просто 1i,

Npoints = 10
points = exp(pi * 1i * seq(0, 2, length.out = Npoints+1)[-1])
plot(points)

Если по какой-либо причине вам необходимо перевести комплекс на декартову плоскость, вы можете извлечь действительные и мнимые компоненты, используя Re() а также Im(),

points.Cartesian = data.frame(x=Re(points), y=Im(points))
Источник 
f <- function(x){
  i <- sqrt(as.complex(-1))
  exp(2*pi*i*x)
}

> f(0/4)
[1] 1+0i
> f(1/4)
[1] 0+1i
> f(2/4)
[1] -1+0i
> f(3/4)
[1] 0-1i

Сказав это, не могли бы вы найти одинаково расположенные точки на окружности, не прибегая к сложным числам?

eq_spacing <- function(n, r = 1){
  polypoints <- seq(0, 2*pi, length.out=n+1)
  polypoints <- polypoints[-length(polypoints)]
  circx <- r * sin(polypoints)
  circy <- r * cos(polypoints)
  data.frame(x=circx, y=circy)
}

eq_spacing(4)
               x             y
 1  0.000000e+00  1.000000e+00
 2  1.000000e+00  6.123032e-17
 3  1.224606e-16 -1.000000e+00
 4 -1.000000e+00 -1.836910e-16

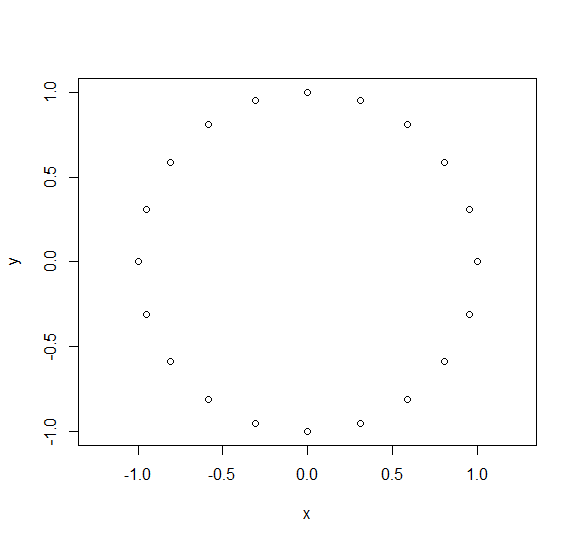
plot(eq_spacing(20), asp = 1)

Источник
Другие вопросы по тегам