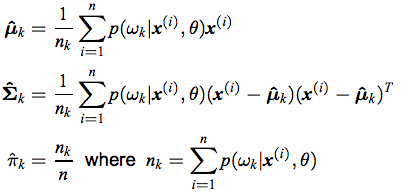Matlab: EM для гауссовых моделей смесей без распределения gm

Question

Я должен тренировать модель гауссовой смеси, используя четыре компонента в данном наборе данных. Набор трехмерный и содержит 300 образцов.

Проблема в том, что я не могу проверить сходимость, используя логарифмическую вероятность, потому что это -Inf, Это следует из округленных нулевых значений при оценке гауссиана в формуле обязанностей (см. E-шаг).

Можете ли вы сказать мне, правильна ли моя реализация алгоритма EM до сих пор? А как объяснить проблему с округленными нулевыми значениями?

Вот моя реализация алгоритма EM (одна итерация):

Сначала я инициализировал средства и ковариацию компонентов, используя kmeans:

load('data1.mat');

X = Data'; % 300x3 data set
D = size(X,2); % dimension
N = size(X,1); % number of samples
K = 4; % number of Gaussian Mixture components

% Initialization
p = [0.2, 0.3, 0.2, 0.3]; % arbitrary pi
[idx,mu] = kmeans(X,K); % initial means of the components

% compute the covariance of the components
sigma = zeros(D,D,K);
for k = 1:K
    sigma(:,:,k) = cov(X(idx==k,:));
end

Для E-шага я использую следующую формулу для расчета ответственности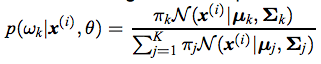

Вот соответствующий код:

gm = zeros(K,N); % gaussian component in the nominator - 
                 % some values evaluate to zero
sumGM = zeros(N,1); % denominator of responsibilities
% E-step:  Evaluate the responsibilities using the current parameters
% compute the nominator and denominator of the responsibilities
for k = 1:K
    for i = 1:N
        % HERE values evalute to zero e.g. exp(-746.6228) = -Inf
        gm(k,i) = p(k)/sqrt(det(sigma(:,:,k))*(2*pi)^D)*exp(-0.5*(X(i,:)-mu(k,:))*inv(sigma(:,:,k))*(X(i,:)-mu(k,:))');
        sumGM(i) = sumGM(i) + gm(k,i);
    end
end
res = zeros(K,N); % responsibilities
Nk = zeros(4,1);
for k = 1:K
    for i = 1:N
         res(k,i) = gm(k,i)/sumGM(i);
    end
    Nk(k) = sum(res(k,:));
end

Nk(k) вычисляется по формуле, приведенной в М-шаге.

М-шаг

% M-step: Re-estimate the parameters using the current responsibilities
mu = zeros(K,3);
for k = 1:K
    for i = 1:N
        mu(k,:) = mu(k,:) + res(k,i).*X(k,:);
        sigma(:,:,k) = sigma(:,:,k) + res(k,i).*(X(k,:)-mu(k,:))*(X(k,:)-mu(k,:))';
    end
    mu(k,:) = mu(k,:)./Nk(k);
    sigma(:,:,k) = sigma(:,:,k)./Nk(k);
    p(k) = Nk(k)/N;
end

Теперь для проверки сходимости логарифмическое правдоподобие вычисляется по следующей формуле:

% Evaluate the log-likelihood and check for convergence of either 
% the parameters or the log-likelihood. If not converged, go to E-step.
loglikelihood = 0;
for i = 1:N
    for k = 1:K
         loglikelihood = loglikelihood + log(gm(k,i));
    end
end

loglikelihood является -Inf потому что некоторые gm(k,i) значения в шаге Е равны нулю. Поэтому бревно явно отрицательная бесконечность.

Как я могу решить эту проблему?

Может ли это быть решено путем увеличения точности Matlab?

Или что-то не так с моей реализацией?

Answer 1

Согласно формуле, вы должны вычислить логарифм суммы величин в г. (итак, лог (сумма (гм (я,:)))). В пределах k компонентов, по крайней мере, один будет иметь вероятность больше 0. Это, надеюсь, решит вашу проблему.

Еще одно очень общее замечание: когда числа слишком велики для функций, как экспоненциальные, и когда вы уверены, что используете правильную формулу, вы всегда можете попытаться поработать с журналом величин. Но вам не нужно делать это здесь, так как 0 - хорошее приближение exp(-746);)