Лучший путь между двумя кривыми

Question

Моя цель состоит в том, чтобы найти гладкую линию наилучшего соответствия между этими двумя изогнутыми фигурами. Есть ли какой-нибудь алгоритм, отличный от моего, который может найти набор точек (или кривую) между двумя линиями, как в этом примере?

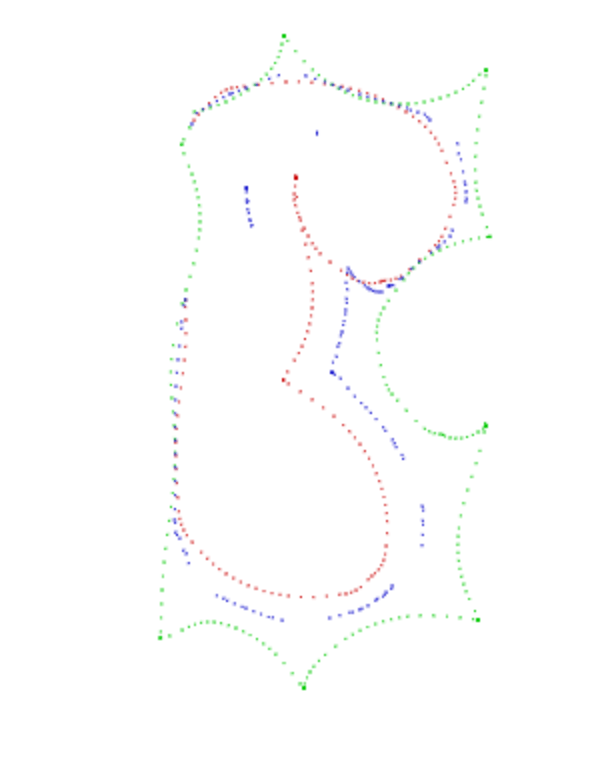
Алгоритм, который у меня есть, занимает внутреннюю часть и для каждой точки находит ближайшую, но это не работает, потому что (посмотрите на первый угол).

(Красный - внутренняя часть, зеленый - внешняя часть, синий - оптимизированные точки, которые я нашел)

Вот мой jsfiddle: http://jsfiddle.net/STLuG/

Это алгоритм:

for (i = 0; i < coords[0].length; i++) {
  var currentI = coords[0][i];
  j = 0;
  var currentJ = coords[0][j];

  currentDist = dist(currentI,currentJ);
  for (j=1; j < coords[1].length; j++) {
    possibleJ = coords[1][j];
    possibleDist = dist(currentI, possibleJ);
    if (possibleDist < currentDist) {
      currentJ = possibleJ;
      currentDist = possibleDist;
    } else {

    }
  }


  b_context.fillRect(
    (currentI.x+currentJ.x)/2+maxX,
    (currentI.y+currentJ.y)/2+maxY,
  1, 1);

}

Спасибо

Answer 1

Я бы попробовал алгоритм наименьших квадратов. У вас есть количество точек: y0 и x0 и y1 и x1 для первой и второй кривой соответственно. Вы хотите найти кривую y (t) и x (t), которая является гладкой и находится между двумя данными кривыми. Таким образом, существует расстояние между первой кривой (x0 (t), y0 (t)) и рассчитываемой вами кривой (x (t), y (t)):

S0 = SumOverAllT (x0 (t) -x (t)) ^2 + (y0 (t) - y (t)) ^ 2

То же самое для второй кривой:

S1 = SumOverAllT (x1(t) -x (t)) ^2 + (y1(t) - y (t)) ^ 2

Сумма обеих сумм:

S = S0 + S1,

У вас будет набор параметров, которые вы хотите определить. Например, если вы используете полиномы:

х (т)= ах + Ьх * T + сх * т ^2 + дх * т ^3....

у (г)= ау + с * т + су * T ^2 + Dy* T ^3....

Затем вы рассчитаете

dS/dax, dS/dbx, dS/dcx, ....

для всех параметров, которые будут рассчитаны

и установите эти производные на ноль:

дс / дакс ==0 дс / дбх ==0 ....

Это даст вам набор линейных уравнений, которые могут быть атакованы алгоритмом Гаусса или любым другим методом для решения системы линейных уравнений.

Если вы используете полиномы, может случиться так, что рассчитанная кривая сильно колеблется. В этом случае я бы предложил попытаться минимизировать интеграл от квадрата второй производной:

I = целое ((d^2x/dt^2)^2 + (d^2y/dt^2)^2, dt)

Вы бы вычислили разницу между I и некоторыми дополнительными параметрами, которые вы не использовали для вышеуказанной системы уравнений - добавление параметра rx и вычисление dI/drx==0 - таким образом, у вас есть еще один параметр и еще одно уравнение.

Любой, кто имеет докторскую степень по математике, пожалуйста, посоветуйте мне любую глупость, о которой я упоминал выше.

Также поищите в интернете:

• Кривая примерка
• Сплайн аппроксимация

Лучшим подходом было бы использовать сплайны - кусочно-непрерывные полиномы, чтобы

• производная 0
• первая производная
• вторая производная

является непрерывным Посмотрите или купите Численные рецепты, чтобы найти код, который делает именно это.

Для сплайн-аппроксимации у вас будет набор полиномов:

x0 (t)= a0x + b0x * (t-t0) + c0x * (t-t0) ^2 + d0x * (t-t0) ^3....

x1(t)= a1x + b1x * (t-t0) + c1x * (t-t0) ^2 + d1x * (t-t0) ^3....

Каждый многочлен будет использоваться только для покрытия соответствия t=t0..t1 между двумя заданными точками.

Затем вы должны добавить уравнения, чтобы убедиться, что значение, первая и вторая производные идентичны для двух соседних полиномов. И установите производную 2 для первого и последнего полинома в ноль.

Потенциально вы можете рассчитать два сплайна - по одному для каждой из двух ваших входных кривых:

х0 (т)

у0 (т)

x1(т)

у1(т)

И тогда вы можете получить середину двух сплайнов:

x (t)= (x0 (t) + (x1(t) -x0 (t)) / 2

y (t)= (y0 (t) + (y1(t) -y0 (t)) / 2

убедитесь, что расстояние между любой из заданных кривых и полученной вами кривой никогда не равно нулю, чтобы они не пересекались друг с другом

Чтобы убедиться, что ваша расчетная линия не пересекает одну из указанных линий, вы можете минимизировать (сумма (сумма (1/(x0-x)^2)) + сумма (сумма (1/(x1-x)^2))))