Должна ли точка на краю многоугольника находиться внутри многоугольника?

Question

Недавно я столкнулся с одной небольшой, но серьезной проблемой: находится ли точка на краю многоугольника внутри многоугольника?

Что я имею в виду - в настоящее время я пытаюсь реализовать библиотеку 2D-геометрии в JS для пользовательских нужд, и есть метод, скажем, polygon.contains (point).

Поэтому мой вопрос - когда точка расположена на одном из ребер многоугольника, - как результат точка находится внутри или снаружи многоугольника? Дополнительный вопрос для вершин: если точка находится сверху вершины многоугольника - это внутри или снаружи?

Алгоритм, который я использовал, взят отсюда и выглядит так:

int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy)
{
    int i, j, c = 0;
    for (i = 0, j = nvert-1; i < nvert; j = i++) {
        if ( ((verty[i]>testy) != (verty[j]>testy)) &&
          (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j] - verty[i]) + vertx[i]) )
           c = !c;
    }
    return c;
}

Также есть цитата с сайта:

PNPOLY разбивает плоскость на точки внутри многоугольника и точки вне многоугольника. Точки, которые находятся на границе, классифицируются как внутри или снаружи.

И это абсолютно верно, в некоторых ситуациях он возвращает TRUE, а в некоторых FALSE.

На самом деле, это не то, что мне нужно. Так что мой вопрос начинает расширяться - какое поведение является правильным, когда точка находится на краю многоугольника - внутри или снаружи. И у вас есть лучший алгоритм с предсказуемым поведением?

ОБНОВИТЬ:

Хорошо, я нашел другой алгоритм, который называется "число обмоток", и для проверки я использую только многоугольники и точки с целочисленными значениями:

function isLeft(p0, p1, p2){
    return ( Math.round((p1.x - p0.x) * (p2.y - p0.y)) - Math.round((p2.x - p0.x) * (p1.y - p0.y)) );
}

function polygonContainsPoint(polygon, point){
    var i, j, pointi, pointj;
    var count = 0;
    var vertices = polygon.vertices;
    var length = vertices.length;
    for (i = 0; i < length; i++){
        j = (i + 1) % length;
        pointi = vertices[i];
        pointj = vertices[j];
        if (pointi.y > point.y){
            if (pointj.y <= point.y && (isLeft(pointi, pointj, point) < 0)){
                --count;
            }
        } else if (pointj.y > point.y && (isLeft(pointi, pointj, point) > 0)){
            ++count;
        }
    }
    return 0 !== count;
}

Как видите, нет разделения; Умножение заключено в метод round(), поэтому нет ошибок для чисел с плавающей запятой. В любом случае, я получаю тот же результат, что и с четно-нечетным алгоритмом. И я думаю, что я начал видеть "образец" в этом странном поведении: левый и верхний края могут указывать, что точка находится внутри многоугольника, но когда вы пытаетесь навести точку на один из правого или нижнего края - это может вернуть ложь.

Это не хорошо для меня. Может быть, некоторые из вас знают какой-то алгоритм с более предсказуемым поведением?

Answer 1

Простой ответ на вопрос состоит в том, что точка на ребре не находится ни внутри, ни снаружи многоугольника, она находится на границе многоугольника - третий вариант. Но обычно это не имеет значения (что подтверждается вашими цитатами), а важно избежать ошибок в классификации точек, которые действительно глубоко внутри или снаружи.

Задачу точки в многоугольнике иногда называют алгоритмом четности:

• Позвольте быть горизонтальной полупрямой, левая конечная точка которой является контрольной точкой.
• Подсчитайте количество пересечений междуrи края многоугольника. Если это число нечетное, то контрольная точка лежит внутри многоугольника, а если число четное, то она находится вне многоугольника.

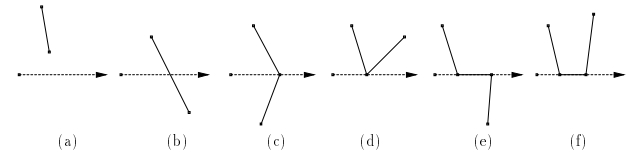
Вот некоторые примеры:

• (а), (б) - невырожденные случаи, когда полупрямая либо не пересекает ребро, либо пересекает его.
• (в), (г), (д), (е) - четыре вырожденных случая, которые необходимо учитывать.

Правильный ответ получается, если случаи (c) и (e) считать за одно пересечение, а случаи (d) и (f) вообще не учитывать. Если мы напишем код для приведенного выше алгоритма, мы поймем, что требуется значительное количество усилий для покрытия четырех вырожденных случаев.

С более сложными алгоритмами и особенно в 3D объем усилий по поддержке вырожденных случаев резко возрастает.

Вышеупомянутая проблема и объяснение появляются во введении к статье Simulation of Simplicity Герберта Эдельсбруннера и Эрнста Петера Муке. И предлагаемое решение состоит в том, чтобы избавиться от всех вырождений путем виртуального минимального возмущения входных точек. После этого проверяемая точка никогда не будет находиться на ребре, а только внутри или снаружи полигона.