Как определить, пересекаются ли два выпуклых многоугольника?
Предположим, что есть несколько выпуклых многоугольников на плоскости, возможно, карта. Эти многоугольники могут сталкиваться друг с другом и иметь общий край, но не могут перекрываться.
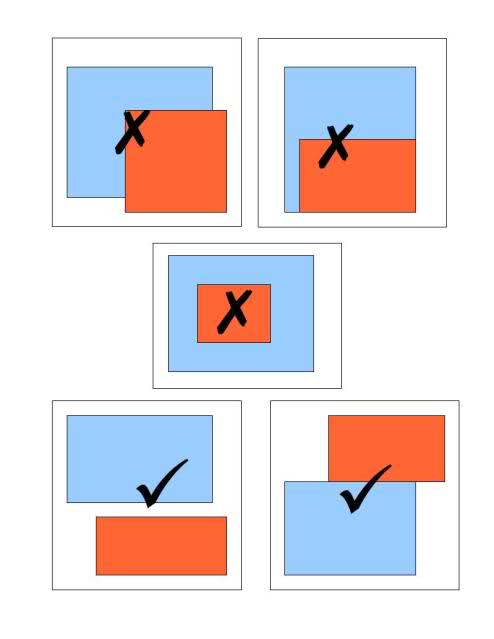
Чтобы проверить, перекрываются ли два многоугольника P и Q, сначала я могу проверить каждое ребро в P, чтобы увидеть, пересекается ли оно с любым из ребер в Q. Если пересечение найдено, я объявляю, что P и Q пересекаются. Если ничего не пересекается, я должен проверить, что P полностью содержится в Q, и наоборот. Далее, есть случай, когда P==Q. Наконец, есть случай, который разделяет несколько ребер, но не все. (Эти два последних случая, вероятно, можно рассматривать как один и тот же общий случай, но это может быть не важно.)
У меня есть алгоритм, который определяет, где пересекаются два отрезка. Если два сегмента коллинеарны, они не считаются пересекающимися для моих целей.
Я правильно перечислил дела? Какие-либо предложения для тестирования в этих случаях?
Обратите внимание, что я не ищу новый выпуклый многоугольник, который является пересечением, я просто хочу знать, существует ли пересечение. Есть много хорошо документированных алгоритмов для поиска пересечения, но мне не нужно прилагать все усилия.
7 ответов
Вы можете использовать этот алгоритм столкновения:
Чтобы определить, пересекаются ли два выпуклых многоугольника (касаясь друг друга), мы можем использовать теорему о разделяющей оси. По существу:
- Если два выпуклых многоугольника не пересекаются, существует линия, проходящая между ними.
- Такая линия существует, только если одна из сторон одного из многоугольников образует такую линию.
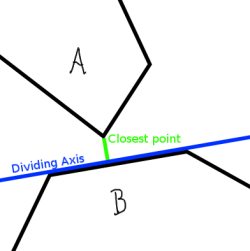
Первое утверждение легко. Поскольку оба многоугольника являются выпуклыми, вы сможете нарисовать линию с одним многоугольником на одной стороне и другим многоугольником на другой стороне, если они не пересекаются. Второй немного менее интуитивно понятен. Посмотрите на рисунок 1. Если самые близкие стороны многоугольников не параллельны друг другу, точка, где они находятся ближе всего друг к другу, - это точка, где угол одного многоугольника становится ближе к стороне другого многоугольника. Эта сторона тогда сформирует разделяющую ось между многоугольниками. Если стороны параллельны, они обе являются разделительными осями.
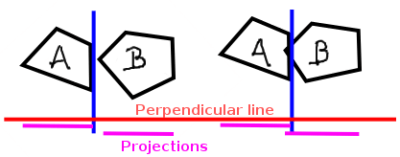
Итак, как это конкретно помогает нам решить, пересекаются ли многоугольники A и B? Ну, мы просто переходим каждую сторону каждого многоугольника и проверяем, образует ли он разделяющую ось. Для этого мы будем использовать некоторую базовую векторную математику, чтобы раздвинуть все точки обоих многоугольников на линию, которая перпендикулярна потенциальной разделительной линии (см. Рисунок 2). Теперь вся задача удобно одномерна. Мы можем определить область, в которой лежат точки для каждого многоугольника, и эта линия является разделительной осью, если эти области не перекрываются.
Если после проверки каждой линии из обоих многоугольников не было найдено разделительной оси, было доказано, что многоугольники пересекаются, и с этим нужно что-то делать.
Существует несколько способов обнаружения пересечения и / или локализации между выпуклыми многоугольниками. Все зависит от того, насколько эффективным вы хотите, чтобы алгоритм был. Рассмотрим два выпуклых многоугольника R и B с r и b вершинами соответственно:
- Алгоритм на основе линии развертки. Как вы упомянули, вы можете выполнить процедуру линии развертки и сохранить интервалы, возникающие в результате пересечения полигонов с линией развертки. Если в любое время интервалы перекрываются, то полигоны пересекаются. Сложность составляет O((r + b) log (r + b)) времени.
- Алгоритм на основе вращающихся штангенциркулей. Смотрите здесь и здесь для более подробной информации. Сложность O(r + b) времени.
- Самые эффективные методы можно найти здесь и здесь. Эти алгоритмы занимают O(log r + log b) время.
если многоугольники всегда выпуклые, сначала вычислите угол линии, проведенной от центра к центру многоугольников. затем вы можете исключить необходимость проверки краевых сегментов в половине многоугольника на расстоянии 180 градусов от другого многоугольника.
чтобы устранить края, начните с многоугольника слева. возьмите отрезок линии от центра многоугольника, который перпендикулярен отрезку линии от предыдущей маркировки, и коснется обеих сторон многоугольника. Назовите этот отрезок линии p с вершинами p1 и p2. Тогда для всех вершин, если координата x меньше p1.x и p2.x, эта вершина может войти в "безопасное ведро".
если это не так, вы должны убедиться, что он находится на "безопасной" стороне линии (просто проверьте координаты y)
- если у отрезка линии в многоугольнике есть все вершины в "безопасном ведре", вы можете проигнорировать это.
- измените полярность, чтобы вы были "ориентированы вправо" для второго многоугольника.
Поскольку altCognito уже дал вам решение, я лишь укажу на отличную книгу по вычислительной геометрии, которая может вас заинтересовать.
Вот идея:
Найти центральную точку каждого многоугольника
Найдите две точки каждого многоугольника, наиболее близкие к центральной точке другой. Они будут смежными точками в выпуклых многоугольниках. Они определяют ближайшее ребро каждого многоугольника, давайте назовем точки {A, B} и {Y, Z}
Найдите пересечение прямых AB и YZ. Если отрезки отрезков пересекаются (пересечение на AB лежит между A и B), ваши полигоны пересекаются. Если AB и XY параллельны, игнорируйте это условие, следующий шаг поймает проблему.
Есть еще один случай, который нужно проверить, когда многоугольники пересекаются достаточно сильно, чтобы AB и XY полностью проходили друг за другом и фактически не пересекались. Чтобы уловить этот случай, вычислите перпендикулярные расстояния AB и XY до центральных точек каждого полигона. Если любая из центральных точек находится ближе к отрезку линии противоположного многоугольника, ваш многоугольник сильно перекрывается.
Ваши тестовые случаи должны работать, так как вы проверяете случай, когда многоугольники вообще не пересекаются (полностью снаружи или полностью внутри), а также где есть какая-либо форма частичного пересечения (ребра пересекаются всегда, если есть перекрытие),
Для тестирования я бы просто проверил каждую потенциальную комбинацию. То, что отсутствует выше из того, что я вижу, является общим ребром, но один поли содержится в другом. Я бы также добавил тесты для некоторых более сложных поли фигур, от трех до трех сторон, просто в качестве меры предосторожности.
Кроме того, если у вас был U-образный поли, который полностью окружал поли, но не перекрывался, я полагаю, что ваш случай справится с этим, но я бы также добавил это в качестве проверки.