Я могу оценить изменяющийся во времени сезонный эффект в R с помощью GAMM?
Я хотел бы использовать обобщенную аддитивную модель для исследования данных временных рядов в R. Мои данные являются ежемесячными, и я хотел бы оценить сезонный эффект и эффект долгосрочного тренда. Я следил за некоторыми полезными постами Гэвина Симпсона здесь и здесь:
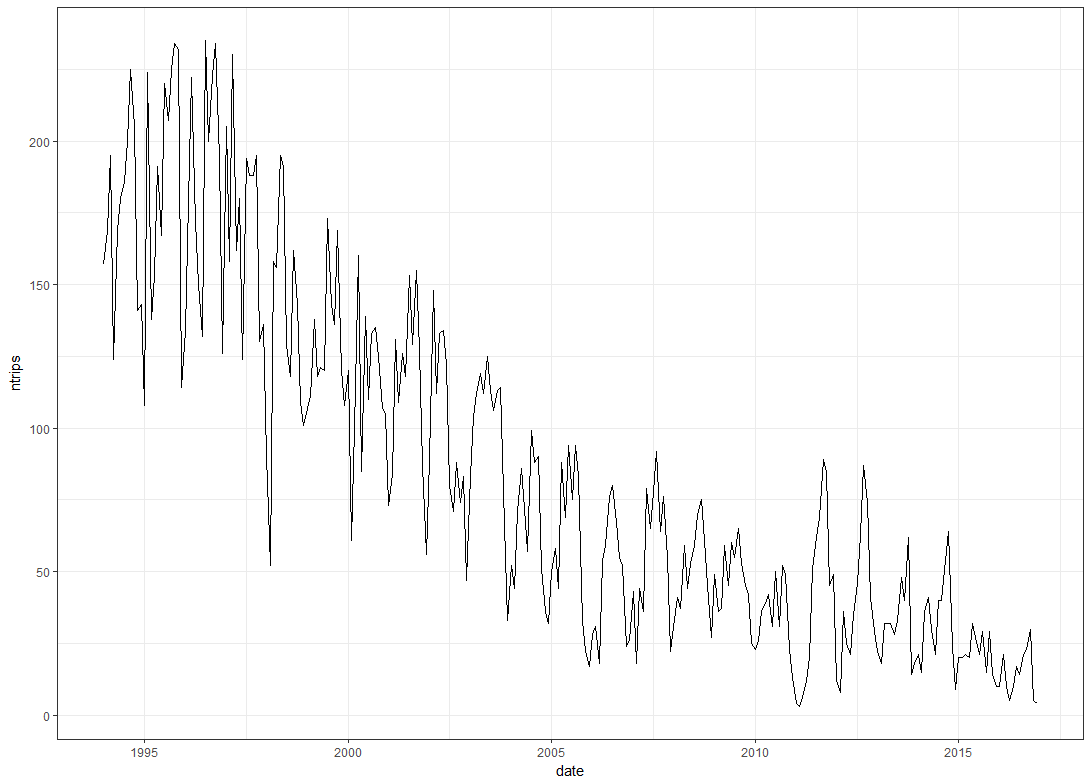
Мои данные выглядят так:
У меня есть полный набор данных, доступных на моей странице GitHub:
Я попытался указать обобщенную аддитивную модель с плавными сезонными и трендовыми терминами следующим образом:
df <- read.csv('trips.csv')
head(df)
# A tibble: 276 × 2
date ntrips
<date> <int>
1 1994-01-01 157
2 1994-02-01 169
3 1994-03-01 195
4 1994-04-01 124
5 1994-05-01 169
#add a time column
trips <- tbl_df(trips) %>% mutate(time=as.numeric(date))
mod1 <- gamm(ntrips~s(month,bs="cc",k=12) + s(time),data=trips)
Я извлек оценку сезонного эффекта следующим образом:
pred <- predict(mod1$gam,newdata=trips,type="terms")
seas <- data.frame(s=pred[,1],date=trips$date)
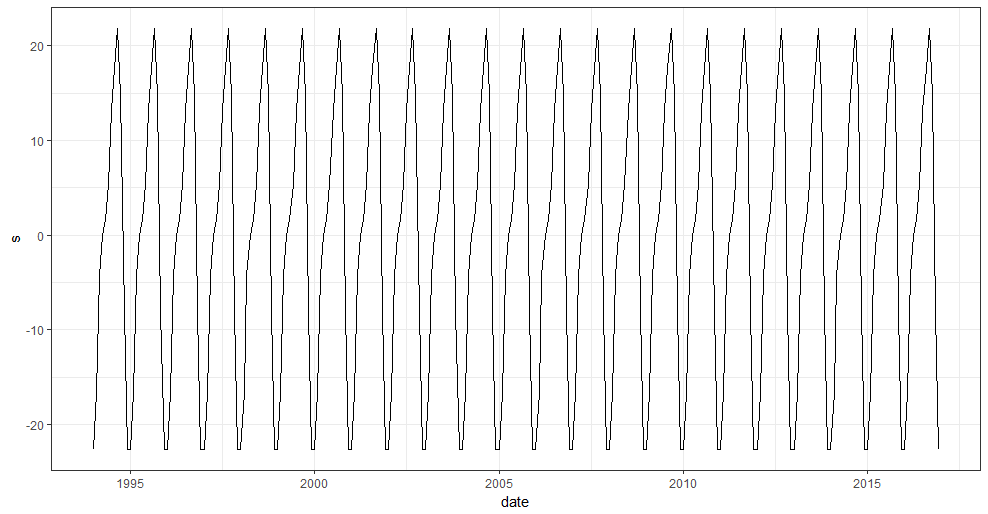
ggplot(seas,aes(x=date,y=s)) + geom_line()
Этот участок включен ниже:
Мой вопрос: в исходных данных сезонные пики немного смещаются из года в год. В смущающе простой GAM, которую я указал, сезонный эффект постоянен. Есть ли способ приспособиться к изменяющейся во времени сезонности с GAM?
Я проанализировал эти данные, используя подход STL Cleveland et al.:
Используя парадигму STL, вопрос о том, насколько волнистым или плавным позволяет сезонный эффект быть, кажется вопросом предпочтения или выбора. Я бы предпочел, если бы я мог позволить данным сказать мне разницу между случайной ошибкой и смещением сезонного пика. GAMS, кажется, лучше подходят для этой цели, так как они более легко поддаются упражнениям статистического моделирования, но я хотел бы знать, есть ли в пакете R параметр для подгонки игровых автоматов, который позволяет варьировать сезонные эффекты во времени.
1 ответ
Ответ таков: да, модель GAM может быть сформулирована для интересующего вас вопроса. Если мы предположим, что трендовые и сезонные компоненты модели взаимодействуют гладко, мы получаем гладкий эквивалент непрерывно-непрерывного взаимодействия. Такое взаимодействие может быть встроено в GAM с использованием тензорного произведения двух краевых сглаживаний:
- сезонное циклическое сглаживание, и
- долгосрочный тренд плавный
Кстати, у меня есть еще сообщения в блоге на эти:
- https://www.fromthebottomoftheheap.net/2015/11/21/climate-change-and-spline-interactions/ и
- https://www.fromthebottomoftheheap.net/2015/11/23/are-some-seasons-warming-more-than-others/
Прочтите их для более подробной информации, но основные аспекты должны соответствовать следующей модели:
## fix the knots are just passed the ends of the month numbers
## this allows Dec and Jan to have their own estimates
knots <- list(month = c(0.5, 12.5))
## original model, fixed seasonal component
m1 <- gam(ntrips ~ s(month, bs="cc", k=12) + s(time), data = trips,
knots = knots)
## modified model with
m2a <- gam(ntrips ~ te(month, time, bs = c("cc","tp"), k = c(12, 10)), data = trips,
knots = knots))
Альтернативой второй модели является ANOVA-подобное разложение двух основных эффектов плюс взаимодействие. В приведенной выше модифицированной модели все три компонента сглажены в едином тензорном произведении: te() часть модели.
ANOVA-подобный вариант разложения будет установлен с использованием
m2b <- gam(ntrips ~ ti(month, bs = 'cc', k = 12) +
ti(time, bs = 'tp', k = 10) +
ti(month, time, bs = c("cc","tp")), data = trips,
knots = knots)
Третий ti() затем происходит плавное взаимодействие, отделенное от основных плавных эффектов сезонного и долгосрочного тренда.
Я показал это с помощью gam() но они могут быть использованы с gamm() также, если вам нужно включить процесс ARMA для остатков модели.