Ближайшая точка на кубической кривой Безье?
Как найти точку B(t) вдоль кубической кривой Безье, ближайшей к произвольной точке P на плоскости?
6 ответов
После долгих поисков я нашел статью, в которой обсуждается метод нахождения ближайшей точки на кривой Безье к данной точке:
Усовершенствованный алгебраический алгоритм точечной проекции для кривых Безье, Сяо-Диао Чен, Инь Чжоу, Женю Шу, Хуа Су и Жан-Клод Пол.
Кроме того, я нашел, что описания последовательностей Штурма в Википедии и MathWorld полезны для понимания первой части алгоритма, поскольку сама статья не очень ясна в своем собственном описании.
Я написал быстрый и грязный код, который оценивает это для кривых Безье любой степени. (Примечание: это псевдо-грубая сила, а не решение в замкнутой форме.)
Демо: http://phrogz.net/svg/closest-point-on-bezier.html
/** Find the ~closest point on a Bézier curve to a point you supply.
* out : A vector to modify to be the point on the curve
* curve : Array of vectors representing control points for a Bézier curve
* pt : The point (vector) you want to find out to be near
* tmps : Array of temporary vectors (reduces memory allocations)
* returns: The parameter t representing the location of `out`
*/
function closestPoint(out, curve, pt, tmps) {
let mindex, scans=25; // More scans -> better chance of being correct
const vec=vmath['w' in curve[0]?'vec4':'z' in curve[0]?'vec3':'vec2'];
for (let min=Infinity, i=scans+1;i--;) {
let d2 = vec.squaredDistance(pt, bézierPoint(out, curve, i/scans, tmps));
if (d2<min) { min=d2; mindex=i }
}
let t0 = Math.max((mindex-1)/scans,0);
let t1 = Math.min((mindex+1)/scans,1);
let d2ForT = t => vec.squaredDistance(pt, bézierPoint(out,curve,t,tmps));
return localMinimum(t0, t1, d2ForT, 1e-4);
}
/** Find a minimum point for a bounded function. May be a local minimum.
* minX : the smallest input value
* maxX : the largest input value
* ƒ : a function that returns a value `y` given an `x`
* ε : how close in `x` the bounds must be before returning
* returns: the `x` value that produces the smallest `y`
*/
function localMinimum(minX, maxX, ƒ, ε) {
if (ε===undefined) ε=1e-10;
let m=minX, n=maxX, k;
while ((n-m)>ε) {
k = (n+m)/2;
if (ƒ(k-ε)<ƒ(k+ε)) n=k;
else m=k;
}
return k;
}
/** Calculate a point along a Bézier segment for a given parameter.
* out : A vector to modify to be the point on the curve
* curve : Array of vectors representing control points for a Bézier curve
* t : Parameter [0,1] for how far along the curve the point should be
* tmps : Array of temporary vectors (reduces memory allocations)
* returns: out (the vector that was modified)
*/
function bézierPoint(out, curve, t, tmps) {
if (curve.length<2) console.error('At least 2 control points are required');
const vec=vmath['w' in curve[0]?'vec4':'z' in curve[0]?'vec3':'vec2'];
if (!tmps) tmps = curve.map( pt=>vec.clone(pt) );
else tmps.forEach( (pt,i)=>{ vec.copy(pt,curve[i]) } );
for (var degree=curve.length-1;degree--;) {
for (var i=0;i<=degree;++i) vec.lerp(tmps[i],tmps[i],tmps[i+1],t);
}
return vec.copy(out,tmps[0]);
}
Приведенный выше код использует библиотеку vmath для эффективного перехода между векторами (в 2D, 3D или 4D), но было бы тривиально заменить lerp() вызывать bézierPoint() с вашим собственным кодом.
Настройка алгоритма
closestPoint() Функция работает в два этапа:
- Сначала вычислите точки по всей кривой (равномерно расположенные значения параметра t). Запишите, какое значение t имеет наименьшее расстояние до точки.
- Затем используйте
localMinimum()функция для поиска области вокруг наименьшего расстояния, используя двоичный поиск, чтобы найти точку и точку, которая дает истинное наименьшее расстояние.
Значение scans в closestPoint() определяет, сколько образцов использовать в первом проходе. Меньше сканирований быстрее, но увеличивает шансы пропустить истинную минимальную точку.
ε предел передан localMinimum() Функция контролирует, как долго она продолжает искать лучшее значение. Значение 1e-2 квантовать кривую в ~100 точек, и, таким образом, вы можете увидеть точки, возвращенные из closestPoint() появляются вдоль линии. Каждая дополнительная десятичная точка точности 1e-3, 1e-4,… - стоит около 6-8 дополнительных звонков bézierPoint(),
Поскольку другие методы на этой странице кажутся приблизительными, этот ответ предоставит простое численное решение. Это реализация на Python в зависимости отnumpy библиотека для поставки Bezierучебный класс. В моих тестах этот подход работал примерно в три раза лучше, чем моя реализация методом грубой силы (с использованием образцов и подразделений).
Посмотрите на интерактивный пример здесь. Нажмите, чтобы увеличить.
Я использовал базовую алгебру, чтобы решить эту минимальную задачу.
Начнем с уравнения кривой Безье.
B(t) = (1 - t)^3 * p0 + 3 * (1 - t)^2 * t * p1 + 3 * (1 - t) * t^2 * p2 + t^3 * p3
Поскольку я использую numpy, мои точки представлены в виде векторов (матриц) numpy. Это значит, чтоp0 является одномерным, например (1, 4.2). Если вы обрабатываете две переменные с плавающей запятой, вам, вероятно, понадобятся несколько уравнений (дляx а также y): Bx(t) = (1-t)^3*px_0 + ...
Преобразуйте его в стандартную форму с четырьмя коэффициентами.
Вы можете записать четыре коэффициента, расширив исходное уравнение.
Расстояние от точки p до кривой B(t) можно вычислить с помощью теоремы Пифагора.
Здесь a и b - два измерения наших точекx а также y. Это означает, что квадрат расстояния D(t) равен:
Я сейчас не вычисляю квадратный корень, потому что этого достаточно, если мы сравним относительные квадраты расстояний. Все следующие уравнения будут относиться к квадрату расстояния.
Эта функция D(t) описывает расстояние между графиком и точками. Нас интересуют минимумы в диапазонеt in [0, 1]. Чтобы найти их, нам нужно дважды получить функцию. Первая производная функции расстояния представляет собой полином 5-го порядка:
Вторая производная:
Граф десмоса позволяет нам исследовать различные функции.
D(t) имеет свои локальные минимумы, где d'(t) = 0 и d' '(t)> = 0. Это означает, что нам нужно найти t для d'(t) = 0'. 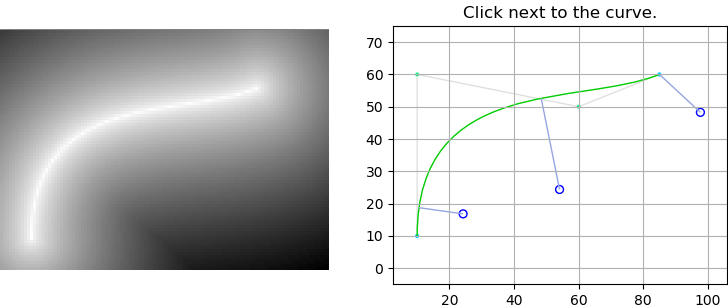
черный: кривая Безье, зеленый: d(t), фиолетовый:d'(t), красный:d''(t)
Найдите корни d '(t). Я использую библиотеку numpy, которая принимает коэффициенты полинома.
dcoeffs = np.stack([da, db, dc, dd, de, df])
roots = np.roots(dcoeffs)
Удалите мнимые корни (оставьте только настоящие корни) и удалите все корни, которые < 0 или > 1. С кубическим безье, вероятно, останется около 0-3 корня.
Затем проверьте расстояния каждого |B(t) - pt| для каждого t in roots. Также проверьте расстояния дляB(0) а также B(1) поскольку начало и конец кривой Безье могут быть ближайшими точками (хотя они не являются локальными минимумами функции расстояния).
Верните ближайшую точку.
Прилагаю класс для Безье на питоне. Проверьте ссылку на github для примера использования.
import numpy as np
# Bezier Class representing a CUBIC bezier defined by four
# control points.
#
# at(t): gets a point on the curve at t
# distance2(pt) returns the closest distance^2 of
# pt and the curve
# closest(pt) returns the point on the curve
# which is closest to pt
# maxes(pt) plots the curve using matplotlib
class Bezier(object):
exp3 = np.array([[3, 3], [2, 2], [1, 1], [0, 0]], dtype=np.float32)
exp3_1 = np.array([[[3, 3], [2, 2], [1, 1], [0, 0]]], dtype=np.float32)
exp4 = np.array([[4], [3], [2], [1], [0]], dtype=np.float32)
boundaries = np.array([0, 1], dtype=np.float32)
# Initialize the curve by assigning the control points.
# Then create the coefficients.
def __init__(self, points):
assert isinstance(points, np.ndarray)
assert points.dtype == np.float32
self.points = points
self.create_coefficients()
# Create the coefficients of the bezier equation, bringing
# the bezier in the form:
# f(t) = a * t^3 + b * t^2 + c * t^1 + d
#
# The coefficients have the same dimensions as the control
# points.
def create_coefficients(self):
points = self.points
a = - points[0] + 3*points[1] - 3*points[2] + points[3]
b = 3*points[0] - 6*points[1] + 3*points[2]
c = -3*points[0] + 3*points[1]
d = points[0]
self.coeffs = np.stack([a, b, c, d]).reshape(-1, 4, 2)
# Return a point on the curve at the parameter t.
def at(self, t):
if type(t) != np.ndarray:
t = np.array(t)
pts = self.coeffs * np.power(t, self.exp3_1)
return np.sum(pts, axis = 1)
# Return the closest DISTANCE (squared) between the point pt
# and the curve.
def distance2(self, pt):
points, distances, index = self.measure_distance(pt)
return distances[index]
# Return the closest POINT between the point pt
# and the curve.
def closest(self, pt):
points, distances, index = self.measure_distance(pt)
return points[index]
# Measure the distance^2 and closest point on the curve of
# the point pt and the curve. This is done in a few steps:
# 1 Define the distance^2 depending on the pt. I am
# using the squared distance because it is sufficient
# for comparing distances and doesn't have the over-
# head of an additional root operation.
# D(t) = (f(t) - pt)^2
# 2 Get the roots of D'(t). These are the extremes of
# D(t) and contain the closest points on the unclipped
# curve. Only keep the minima by checking if
# D''(roots) > 0 and discard imaginary roots.
# 3 Calculate the distances of the pt to the minima as
# well as the start and end of the curve and return
# the index of the shortest distance.
#
# This desmos graph is a helpful visualization.
# https://www.desmos.com/calculator/ktglugn1ya
def measure_distance(self, pt):
coeffs = self.coeffs
# These are the coefficients of the derivatives d/dx and d/(d/dx).
da = 6*np.sum(coeffs[0][0]*coeffs[0][0])
db = 10*np.sum(coeffs[0][0]*coeffs[0][1])
dc = 4*(np.sum(coeffs[0][1]*coeffs[0][1]) + 2*np.sum(coeffs[0][0]*coeffs[0][2]))
dd = 6*(np.sum(coeffs[0][0]*(coeffs[0][3]-pt)) + np.sum(coeffs[0][1]*coeffs[0][2]))
de = 2*(np.sum(coeffs[0][2]*coeffs[0][2])) + 4*np.sum(coeffs[0][1]*(coeffs[0][3]-pt))
df = 2*np.sum(coeffs[0][2]*(coeffs[0][3]-pt))
dda = 5*da
ddb = 4*db
ddc = 3*dc
ddd = 2*dd
dde = de
dcoeffs = np.stack([da, db, dc, dd, de, df])
ddcoeffs = np.stack([dda, ddb, ddc, ddd, dde]).reshape(-1, 1)
# Calculate the real extremes, by getting the roots of the first
# derivativ of the distance function.
extrema = np_real_roots(dcoeffs)
# Remove the roots which are out of bounds of the clipped range [0, 1].
# [future reference] https://stackru.com/questions/47100903/deleting-every-3rd-element-of-a-tensor-in-tensorflow
dd_clip = (np.sum(ddcoeffs * np.power(extrema, self.exp4)) >= 0) & (extrema > 0) & (extrema < 1)
minima = extrema[dd_clip]
# Add the start and end position as possible positions.
potentials = np.concatenate((minima, self.boundaries))
# Calculate the points at the possible parameters t and
# get the index of the closest
points = self.at(potentials.reshape(-1, 1, 1))
distances = np.sum(np.square(points - pt), axis = 1)
index = np.argmin(distances)
return points, distances, index
# Point the curve to a matplotlib figure.
# maxes ... the axes of a matplotlib figure
def plot(self, maxes):
import matplotlib.path as mpath
import matplotlib.patches as mpatches
Path = mpath.Path
pp1 = mpatches.PathPatch(
Path(self.points, [Path.MOVETO, Path.CURVE4, Path.CURVE4, Path.CURVE4]),
fc="none")#, transform=ax.transData)
pp1.set_alpha(1)
pp1.set_color('#00cc00')
pp1.set_fill(False)
pp2 = mpatches.PathPatch(
Path(self.points, [Path.MOVETO, Path.LINETO , Path.LINETO , Path.LINETO]),
fc="none")#, transform=ax.transData)
pp2.set_alpha(0.2)
pp2.set_color('#666666')
pp2.set_fill(False)
maxes.scatter(*zip(*self.points), s=4, c=((0, 0.8, 1, 1), (0, 1, 0.5, 0.8), (0, 1, 0.5, 0.8),
(0, 0.8, 1, 1)))
maxes.add_patch(pp2)
maxes.add_patch(pp1)
# Wrapper around np.roots, but only returning real
# roots and ignoring imaginary results.
def np_real_roots(coefficients, EPSILON=1e-6):
r = np.roots(coefficients)
return r.real[abs(r.imag) < EPSILON]
В зависимости от ваших допусков. Грубая сила и принятие ошибки. Этот алгоритм может быть неправильным в некоторых редких случаях. Но в большинстве из них он найдет точку, очень близкую к правильному ответу, и результаты будут тем лучше, чем выше вы установите срезы. Он просто проверяет каждую точку вдоль кривой через равные промежутки времени и возвращает лучшую найденную точку.
public double getClosestPointToCubicBezier(double fx, double fy, int slices, double x0, double y0, double x1, double y1, double x2, double y2, double x3, double y3) {
double tick = 1d / (double) slices;
double x;
double y;
double t;
double best = 0;
double bestDistance = Double.POSITIVE_INFINITY;
double currentDistance;
for (int i = 0; i <= slices; i++) {
t = i * tick;
//B(t) = (1-t)**3 p0 + 3(1 - t)**2 t P1 + 3(1-t)t**2 P2 + t**3 P3
x = (1 - t) * (1 - t) * (1 - t) * x0 + 3 * (1 - t) * (1 - t) * t * x1 + 3 * (1 - t) * t * t * x2 + t * t * t * x3;
y = (1 - t) * (1 - t) * (1 - t) * y0 + 3 * (1 - t) * (1 - t) * t * y1 + 3 * (1 - t) * t * t * y2 + t * t * t * y3;
currentDistance = Point.distanceSq(x,y,fx,fy);
if (currentDistance < bestDistance) {
bestDistance = currentDistance;
best = t;
}
}
return best;
}
Вы можете стать намного лучше и быстрее, просто находя ближайшую точку и возвращаясь к этой точке.
public double getClosestPointToCubicBezier(double fx, double fy, int slices, int iterations, double x0, double y0, double x1, double y1, double x2, double y2, double x3, double y3) {
return getClosestPointToCubicBezier(iterations, fx, fy, 0, 1d, slices, x0, y0, x1, y1, x2, y2, x3, y3);
}
private double getClosestPointToCubicBezier(int iterations, double fx, double fy, double start, double end, int slices, double x0, double y0, double x1, double y1, double x2, double y2, double x3, double y3) {
if (iterations <= 0) return (start + end) / 2;
double tick = (end - start) / (double) slices;
double x, y, dx, dy;
double best = 0;
double bestDistance = Double.POSITIVE_INFINITY;
double currentDistance;
double t = start;
while (t <= end) {
//B(t) = (1-t)**3 p0 + 3(1 - t)**2 t P1 + 3(1-t)t**2 P2 + t**3 P3
x = (1 - t) * (1 - t) * (1 - t) * x0 + 3 * (1 - t) * (1 - t) * t * x1 + 3 * (1 - t) * t * t * x2 + t * t * t * x3;
y = (1 - t) * (1 - t) * (1 - t) * y0 + 3 * (1 - t) * (1 - t) * t * y1 + 3 * (1 - t) * t * t * y2 + t * t * t * y3;
dx = x - fx;
dy = y - fy;
dx *= dx;
dy *= dy;
currentDistance = dx + dy;
if (currentDistance < bestDistance) {
bestDistance = currentDistance;
best = t;
}
t += tick;
}
return getClosestPointToCubicBezier(iterations - 1, fx, fy, Math.max(best - tick, 0d), Math.min(best + tick, 1d), slices, x0, y0, x1, y1, x2, y2, x3, y3);
}
В обоих случаях вы можете сделать четырехугольник так же легко:
x = (1 - t) * (1 - t) * x0 + 2 * (1 - t) * t * x1 + t * t * x2; //quad.
y = (1 - t) * (1 - t) * y0 + 2 * (1 - t) * t * y1 + t * t * y2; //quad.
Переключив уравнение там.
Хотя принятый ответ правильный, и вы действительно можете выяснить корни и сравнить эти вещи. Если вам действительно нужно найти ближайшую точку на кривой, это сделает это.
По поводу Бена в комментариях. Вы не можете сократить формулу во многих сотнях контрольных точек, как я сделал для кубических и четырехугольных форм. Потому что количество, требуемое каждым новым добавлением кривой Безье, означает, что вы строите для них пифагорейские пирамиды, и мы в основном имеем дело с еще более и более массивными цепочками чисел. Для четырехугольника вы идете 1, 2, 1, для кубического - 1, 3, 3, 1. В конечном итоге вы строите все большие и большие пирамиды и разбиваете их с помощью алгоритма Кастельжау (я написал это для полной скорости):
/**
* Performs deCasteljau's algorithm for a bezier curve defined by the given control points.
*
* A cubic for example requires four points. So it should get at least an array of 8 values
*
* @param controlpoints (x,y) coord list of the Bezier curve.
* @param returnArray Array to store the solved points. (can be null)
* @param t Amount through the curve we are looking at.
* @return returnArray
*/
public static float[] deCasteljau(float[] controlpoints, float[] returnArray, float t) {
int m = controlpoints.length;
int sizeRequired = (m/2) * ((m/2) + 1);
if (returnArray == null) returnArray = new float[sizeRequired];
if (sizeRequired > returnArray.length) returnArray = Arrays.copyOf(controlpoints, sizeRequired); //insure capacity
else System.arraycopy(controlpoints,0,returnArray,0,controlpoints.length);
int index = m; //start after the control points.
int skip = m-2; //skip if first compare is the last control point.
for (int i = 0, s = returnArray.length - 2; i < s; i+=2) {
if (i == skip) {
m = m - 2;
skip += m;
continue;
}
returnArray[index++] = (t * (returnArray[i + 2] - returnArray[i])) + returnArray[i];
returnArray[index++] = (t * (returnArray[i + 3] - returnArray[i + 1])) + returnArray[i + 1];
}
return returnArray;
}
В основном вам нужно использовать алгоритм напрямую, не только для вычисления x,y, которые происходят на самой кривой, но вам также нужно, чтобы он выполнял действительный и правильный алгоритм подразделения Безье (есть другие, но это то, что я хотел бы рекомендую), чтобы рассчитать не только приближение, которое я даю, разделив его на отрезки, но и действительные кривые. Или скорее корпус многоугольника, который наверняка будет содержать кривую.
Вы делаете это, используя вышеупомянутый алгоритм, чтобы подразделить кривые в данном t. Таким образом, T=0,5, чтобы разрезать кривые пополам (примечание 0.2 сократило бы его на 20%, 80% по кривой). Затем вы индексируете различные точки на стороне пирамиды и на другой стороне пирамиды, построенной из основания. Так, например, в куб.
9
7 8
4 5 6
0 1 2 3
Вы должны указать алгоритм 0 1 2 3 в качестве контрольных точек, а затем индексировать две идеально разделенные кривые на 0, 4, 7, 9 и 9, 8, 6, 3. Обратите особое внимание на то, что эти кривые начинаются и заканчиваются в той же точке. и последний индекс 9, который является точкой на кривой, используется в качестве другой новой точки привязки. Учитывая это, вы можете идеально разделить кривую Безье.
Затем, чтобы найти ближайшую точку, вы хотите продолжить подразделение кривой на разные части, отмечая, что это тот случай, когда вся кривая Безье содержится внутри корпуса контрольных точек. То есть, если мы превращаем точки 0, 1, 2, 3 в замкнутый путь, соединяющий 0,3, эта кривая должна полностью попадать в этот корпус многоугольника. Таким образом, мы определяем заданную точку P, затем продолжаем подразделять кривые до тех пор, пока не узнаем, что самая дальняя точка одной кривой находится ближе, чем самая близкая точка другой кривой. Мы просто сравниваем эту точку P со всеми контрольными и опорными точками кривых. И отбросьте любую кривую из нашего активного списка, ближайшая точка которой (привязка или элемент управления) находится дальше, чем самая дальняя точка другой кривой. Затем мы подразделяем все активные кривые и делаем это снова. В конечном итоге у нас будут очень подразделенные кривые, отбрасывающие примерно половину каждого шага (то есть, это должно быть O(n log n)), пока наша ошибка в основном незначительна. В этой точке мы называем наши активные кривые ближайшей точкой к этой точке (их может быть больше одной) и отмечаем, что ошибка в этом сильно подразделенном бите кривой в основном равна точке. Или просто решите проблему, сказав, какая из двух опорных точек ближе всего находится к нашей точке P. И мы знаем ошибку в очень определенной степени.
Это, однако, требует, чтобы мы на самом деле имели надежное решение и выполнили, безусловно, правильный алгоритм и правильно нашли крошечную часть кривой, которая, безусловно, будет ближайшей точкой к нашей точке. И все еще должно быть относительно быстро.
Существуют также специфичные для DOM SVG реализации алгоритмов ближайших точек от Майка Бостока:
Решением этой проблемы было бы получить все возможные точки на кривой Безье и сравнить каждое расстояние. Количество точек можно контролировать с помощью переменной detail.
Вот реализация, сделанная в Unity (C#):
public Vector2 FindNearestPointOnBezier(Bezier bezier, Vector2 point)
{
float detail = 100;
List<Vector2> points = new List<Vector2>();
for (float t = 0; t < 1f; t += 1f / detail)
{
// this function can be exchanged for any bezier curve
points.Add(Functions.CalculateBezier(bezier.a, bezier.b, bezier.c, bezier.d, t));
}
Vector2 closest = Vector2.zero;
float minDist = Mathf.Infinity;
foreach (Vector2 p in points)
{
// use sqrMagnitude as it is faster
float dist = (p - point).sqrMagnitude;
if (dist < minDist)
{
minDist = dist;
closest = p;
}
}
return closest;
}
Обратите внимание, что класс Безье содержит всего 4 балла.