2D Упругая Шариковая Физика

Question

2D Упругая Шариковая Физика

Я делаю программу, которая включает физику упругих шаров. Я разработал всю математику для столкновения со стенами и стационарными объектами, но я не могу понять, что происходит, когда сталкиваются два движущихся шара. У меня есть масса и скорость (скорость x и y, если быть точным, но скорость каждого шара и их направление подойдут), и я хотел бы получить формулы для них. Помните - это идеально упругое столкновение - поэтому нет вращающихся шариков и т. Д.

13

2d physics collision

Источник

user5885184 04 фев '16 в 20:36

1 ответ

Другие вопросы по тегам 2d physics collision

user5805330 04 фев '16 в 22:11 2016-02-04 22:11 · Answer 1 · 2016-02-04 22:11

Эта статья в Википедии предоставляет формулу для расчета скоростей после столкновения двух частиц:

$\ mathbf {v'_1} = \ mathbf {v_1} - \ frac {2m_2} {m_1 + m_2} \ frac {\ left \ langle \ mathbf {v_1} - \ mathbf {v_2} | \ mathbf {x_1} - \ mathbf {x_2} \ right \ rangle} {{\ left \ | \ mathbf {x_1} - \ mathbf {x_2} \ right \ |} ^ {2}} (\ mathbf {x_1} - \ mathbf {x_2})$

$\ mathbf {v'_2} = \ mathbf {v_2} - \ frac {2m_1} {m_1 + m_2} \ frac {\ left \ langle \ mathbf {v_2} - \ mathbf {v_1} | \ mathbf {x_2} - \ mathbf {x_1} \ right \ rangle} {{\ left \ | \ mathbf {x_2} - \ mathbf {x_1} \ right \ |} ^ {2}} (\ mathbf {x_2} - \ mathbf {x_1})$

Есть много причин использовать эту формулу:

вам просто нужны векторы скорости ваших шаров до столкновения, их масса и их положение,
вам не нужно определять углы отклонения,
операции просты (требуется только точка продукта),
векторы могут быть выражены в любой системе координат.

В статье Википедии нет никаких доказательств, поэтому я приведу их ниже.

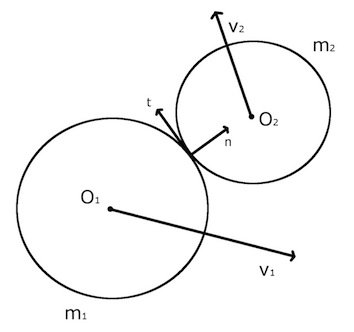
Определение проблемы

Для каждого шара мы определяем:

ми масса
vi вектор скорости до столкновения
v'i вектор скорости после столкновения
Ой точка центра
xi вектор положения Oi

Единичный вектор n нормален к поверхности шариков в точке контакта.

$\ mathbf {n} = \ frac {\ mathbf {O_1O_2}} {\ left \ | \ mathbf {O_1O_2} \ right \ |} = \ frac {\ mathbf {x_2 - x_1}} {\ left \ | \ mathbf {x_2 - x_1} \ right \ |}$

Единичный вектор t касается поверхностей шариков в точке контакта.

Физический закон для использования

Сохранение полного импульса выражается:

$m_1 \ mathbf {v'_1} + m_2 \ mathbf {v'_2} = m_1 \ mathbf {v_1} + m_2 \ mathbf {v_2}$

Сохранение полной кинетической энергии выражается:

$\ frac {m_1 {v '} _ 1 ^ {2}} {2} + \ frac {m_2 {v'} _ 2 ^ {2}} {2} = \ frac {m_1 v_1 ^ {2}} {2} + \ frac {m_2 v_2 ^ {2}} {2}$

Поскольку в тангенциальном направлении сила не приложена, тангенциальные составляющие скоростей остаются неизменными после столкновения:

$\ left \ {\ begin {matrix} \ left \ langle \ mathbf {v'_1} | \ mathbf {t} \ right \ rangle = \ left \ langle \ mathbf {v_1} | \ mathbf {t} \ right \ rangle \\ \ left \ langle \ mathbf {v'_2} | \ mathbf {t} \ right \ rangle = \ left \ langle \ mathbf {v_2} | \ mathbf {t} \ right \ rangle \ end {matrix} \ right,$

доказательство

Тангенциальные составляющие скоростей неизменны. Таким образом, мы можем переписать законы сохранения с нормальными компонентами, и теперь у нас есть 1D проблема:

$\ left \ {\ begin {matrix} m_1 {\ left \ langle \ mathbf {v'_1} | \ mathbf {n} \ right \ rangle} + m_2 {\ left \ langle \ mathbf {v'_2} | \ mathbf {n} \ right \ rangle} = m_1 {\ left \ langle \ mathbf {v_1} | \ mathbf {n} \ right \ rangle} + m_2 {\ left \ langle \ mathbf {v_2} | \ mathbf {n} \ right \ rangle} \\ m_1 {\ left \ langle \ mathbf {v'_1} | \ mathbf {n} \ right \ rangle} ^ {2} + m_2 {\ left \ langle \ mathbf {v'_2} | \ mathbf {n} \ right \ rangle} ^ {2} = m_1 {\ left \ langle \ mathbf {v_1} | \ mathbf {n} \ right \ rangle} ^ {2} + m_2 {\ left \ langle \ mathbf { v_2} | \ mathbf {n} \ right \ rangle} ^ {2} \ end {matrix} \ right.$

Сохранение кинетической энергии может быть факторизовано, а затем упрощено с сохранением импульса:

$m_1 {\ left \ langle \ mathbf {v'_1} | \ mathbf {n} \ right \ rangle} ^ {2} -m_1 {\ left \ langle \ mathbf {v_1} | \ mathbf {n} \ right \ rangle } ^ {2} = m_2 {\ left \ langle \ mathbf {v_2} | \ mathbf {n} \ right \ rangle} ^ {2} -m_2 {\ left \ langle \ mathbf {v'_2} | \ mathbf { n} \ right \ rangle} ^ {2}$

$\ Rightarrow {\ left \ langle \ mathbf {v'_1} | \ mathbf {n} \ right \ rangle} + {\ left \ langle \ mathbf {v_1} | \ mathbf {n} \ right \ rangle} = {\ left \ langle \ mathbf {v_2} | \ mathbf {n} \ right \ rangle} + {\ left \ langle \ mathbf {v'_2} | \ mathbf {n} \ right \ rangle}$

Мы объединяем это последнее выражение с сохранением импульса и получаем нормальную составляющую v'1:

$\ left \ langle \ mathbf {v'_1} | \ mathbf {n} \ right \ rangle = \ frac {(m_1-m_2) \ left \ langle \ mathbf {v_1} | \ mathbf {n} \ right \ rangle + 2 m_2 \ left \ langle \ mathbf {v_2} | \ mathbf {n} \ right \ rangle} {m_1 + m_2} = \ left \ langle \ mathbf {v_1} | \ mathbf {n} \ right \ rangle- \ frac {2 m_2 \ left \ langle \ mathbf {v_1-v_2} | \ mathbf {n} \ right \ rangle} {m_1 + m_2}$

Наконец, мы находим формулу статьи в Википедии для v'1:

$\ mathbf {v'_1} = \ left \ langle \ mathbf {v'_1} | \ mathbf {n} \ right \ rangle \ mathbf {n} + \ left \ langle \ mathbf {v'_1} | \ mathbf {t} \ right \ rangle \ mathbf {t} = \ mathbf {v_1} - \ frac {2m_2} {m_1 + m_2} \ frac {\ left \ langle \ mathbf {v_1} - \ mathbf {v_2} | \ mathbf {x_1} - \ mathbf {x_2} \ right \ rangle} {{\ left \ | \ mathbf {x_1} - \ mathbf {x_2} \ right \ |} ^ {2}} (\ mathbf {x_1} - \ mathbf {x_2})$

Формула v'2 симметрична.

user2381899 11 июл '20 в 22:08 2020-07-11 22:08 · Answer 2 · 2020-07-11 22:08

Поскольку я делаю римейк на blobby, тела не обязательно являются шарами - углы попадания не связаны с расстоянием между X1,X2. Поэтому я использовал следующие уравнения: https://williamecraver.wixsite.com/elastic-equations

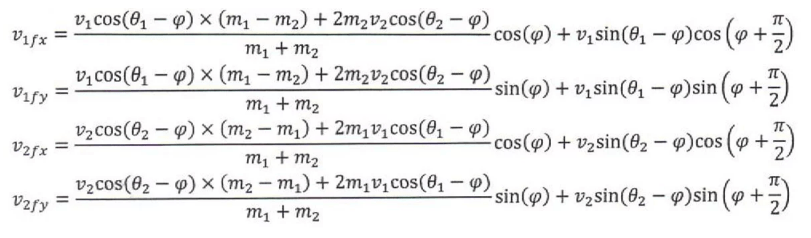
Ниже приведен код, который вычисляет векторный угол из скоростей dx dy: Далее ниже приведены уравнения (которые требуют преобразованного векторного ввода). код находится в Python 3.8x. Кортежи являются входными и выходными для функций.

def angle_ofdxdy(dxdy):  # returns angle, z
  dx, dy = dxdy[0], dxdy[1]
  if abs(dy) < 0.01: #prevent div by zero
    dy = 0.01
  # https://math.stackexchange.com/questions/1327253/how-do-we-find-out-angle-from-x-y-coordinates
  z = (dx ** 2 + dy ** 2) ** 0.5
  angle = 2 * atan(dy / (dx + z))
  return (round(angle, 4), z)

ниже представлена функция подготовки, которая использует вышеуказанное перед вызовом уравнений:

def calc_impulse_xy1xy2(xy1_xy2, ball_mass=1, wall_mass=10000000, gamma=0):
  xy1, xy2 = xy1_xy2
  a1, z = angle_ofdxdy(xy1)
  a2, z2 = angle_ofdxdy(xy2)
  # print(f'xy xy translator called for xy={xy1}, xy2{xy2}, angles {degrees(a1):.0f},  {degrees(a2):.0f}')
  return cv1v2(z, a1, z2, a2, ball_mass, wall_mass, gamma)

ниже приведены фактические уравнения:

def cv1v2(ball_velocity=5, ball_theta=0, wall_velocity=0, wall_theta=0, ball_mass=1, wall_mass=10000000, gamma=0):
  g = gamma  # 0 needs further explainig. ba
  t1,t2 = ball_theta, wall_theta
  v1,v2 = ball_velocity, wall_velocity  # a scalar.
  m1,m2 = ball_mass, wall_mass

  # print('pi/2 is',pi/2)
  vx = (v1 * cos(t1 - g) * (m1 - m2) + 2 * m2 * v2 * cos(t2 - g)) * cos(g) / (m1 + m2) + v1 * sin(t1 - g) * cos(g + pi / 2)
  vy = (v1 * cos(t1 - g) * (m1 - m2) + 2 * m2 * v2 * cos(t2 - g)) * sin(g) / (m1 + m2) + v1 * sin(t1 - g) * sin(g + pi / 2)
  v2x = (v2 * cos(t2 - g) * (m2 - m1) + 2 * m1 * v1 * cos(t1 - g)) * cos(g) / (m1 + m2) + v2 * sin(t2 - g) * cos(g + pi / 2)
  v2y = (v2 * cos(t2 - g) * (m2 - m1) + 2 * m1 * v1 * cos(t1 - g)) * sin(g) / (m1 + m2) + v2 * sin(t2 - g) * sin(g + pi / 2)
  xyxy = ((round(vx, 2), round(vy, 2)), (round(v2x, 2), round(v2y, 2)))
  print(f'Ball: {v1:.1f}({degrees(t1):.0f}\u2070)\t Player:{v2:.1f}({degrees(t2):.0f}\u2070),  impact angle:{degrees(g):.0f}\u2070 masses:{m1},{m2} \nresult:{xyxy}')
  return xyxy

Функция относится к мячу и стене. Это просто подсказка на тот случай, если вы хотите протестировать отскок от стены, используя те же уравнения (по умолчанию второму объекту назначен большой вес). Конечно, вы можете поместить идентичные массы в вызов функции. Проверено. За работой

Этот подход предполагает, что вы рассчитали гамму - угол контакта. Это очень просто, если у вас есть полная информация о точке столкновения и форме ваших объектов. Особенно, если хотя бы один мяч