Теорема о разделении MVT вдоль только одной оси

Question

У меня проблемы с вычислением трехмерного вектора проникновения вдоль одной оси. Я уже внедрил SAT, и это работает. Я хочу подсчитать, сколько мне нужно, чтобы сместить первую рамку от другой, чтобы она всегда стояла поверх другой. Вроде делали простую коробку с очень длинной коробкой.

Как я должен продолжить поиск смещения, которое будет толкать один объект в направлении указанной оси.

Answer 1

Первая часть этого вы уже должны знать; когда вы проецируете каждую фигуру на каждую ось, должно быть некоторое минимальное и максимальное скалярное значение для формы A, скажем, AMIN а также AMAXи то же самое для формы B (BMIN / BMAX).

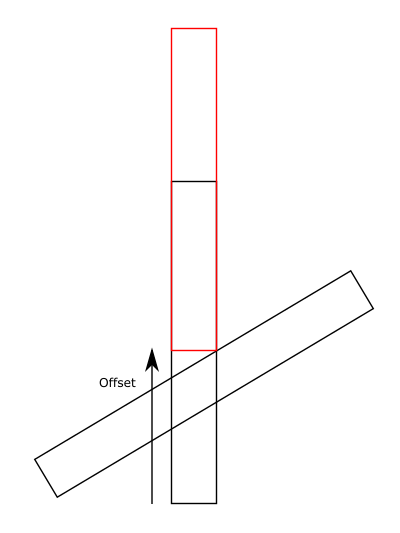
Если объекты явно сталкиваются на оси, их проекции будут перекрываться, что означает либо AMIN < BMIN < AMAX < BMAX или же BMIN < AMIN < BMAX < AMAX, Давайте предположим первое.

Значение AMAX-BMIN это расстояние, необходимое для перемещения любой фигуры, чтобы привести их в соприкосновение, а тестируемая ось дает вам направление.

Обычно, когда кто-то проходит по всем осям, он отслеживает минимальное значение и соответствующую ему ось, и это становится вектором, необходимым для разборки фигур. (Обычно называется "вектор минимального смещения", если вы хотите, чтобы Google его.)

Для вас, желая сместить их в определенном направлении, вы просто сохраните значение, соответствующее этой конкретной оси, и оно станет вашим вектором смещения (который затем будет добавлен к позиции одной фигуры для их разделения).

Я настоятельно рекомендую Googling "минимальное смещение вектора смещения" и ознакомьтесь с несколькими первыми ссылками, а именно с этой: http://www.dyn4j.org/2010/01/sat/. Это немного плотно, но здесь я узнал все, что знаю о SAT.

РЕДАКТИРОВАТЬ И... Я пропустил кусок. Это довольно грубо, но если вы хотите сместить фигуры вдоль одной оси (в вашем примере - по вертикали), основываясь на векторе смещения, полученном от другой оси (нормали длинной стороны нижнего прямоугольника), вам нужно спроецируйте вектор смещения на нужную (нормализованную) ось (используя точечное произведение), чтобы получить правильное расстояние, затем объедините с нужной осью.