Лучше всего подходит квадрат от четырехугольника
У меня есть фигура, состоящая из четырех точек, A, B, C и D, из которых известна только их позиция. Цель состоит в том, чтобы преобразовать эти точки, чтобы иметь определенные углы и смещения относительно друг друга.
Например: A(-1,-1) B(2,-1) C(1,1) D(-2,1), который должен быть преобразован в идеальный квадрат (все углы 90) со смещениями между AB, BC, CD и AD, равными 2. Результат должен быть квадратом, слегка повернутым против часовой стрелки.
Какой самый эффективный способ сделать это? Я использую это для простой программы моделирования блоков.
2 ответа
Как намекает Марк, мы можем использовать ограниченную оптимизацию, чтобы найти квадрат стороны 2, который минимизирует квадрат расстояния до углов оригинала.
Нам нужно минимизировать f = (a-A)^2 + (b-B)^2 + (c-C)^2 + (d-D)^2 (где квадрат на самом деле является точечным произведением векторного аргумента с самим собой) с учетом некоторых ограничений.
Следуя методу множителей Лагранжа, я выбрал следующие ограничения расстояния:
g1 = (a-b)^2 - 4
g2 = (c-b)^2 - 4
g3 = (d-c)^2 - 4
и следующие угловые ограничения:
g4 = (b-a).(c-b)
g5 = (c-b).(d-c)
Быстрый набросок салфетки должен убедить вас, что этих ограничений достаточно.
Затем мы хотим минимизировать f при условии, что все g равны нулю.
Функция Лагранжа:
L = f + Sum (i = 1 - 5, li gi)
где lis - множители Лагранжа.
Градиент нелинейный, поэтому мы должны взять гессиан и использовать многомерный метод Ньютона для итерации к решению.
Вот решение, которое я получил (красный) для данных данных (черный):
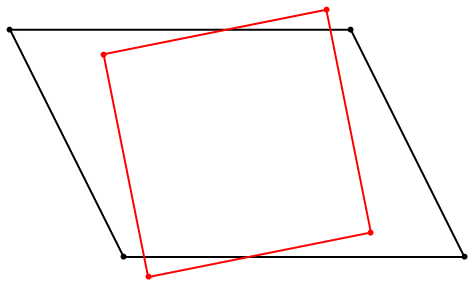
Это заняло 5 итераций, после чего L2 норма шага была 6,5106e-9.
Хотя решение Codie CodeMonkey является совершенно правильным (и отличным вариантом использования множителей Лагранжа), я считаю, что стоит упомянуть, что если длина стороны не задана, эта конкретная проблема фактически имеет решение в закрытой форме .
Мы хотели бы минимизировать расстояние между углами нашего подогнанного квадрата и углами данного четырехугольника. Это эквивалентно минимизации функции стоимости:
f(x1,...,y4) = (x1-ax)^2+(y1-ay)^2 + (x2-bx)^2+(y2-by)^2 +
(x3-cx)^2+(y3-cy)^2 + (x4-dx)^2+(y4-dy)^2
Где
Pi = (xi,yi) углы подогнанного квадрата и
A = (ax,ay) через
D = (dx,dy)представляют собой заданные углы четырехугольника. Поскольку мы устанавливаем квадрат, у нас есть определенные ограничения относительно положения четырех углов. На самом деле, если даны два противоположных угла, их достаточно, чтобы описать уникальный квадрат (за исключением зеркального отображения по диагонали).
Это означает, что двух противоположных углов достаточно, чтобы представить наш целевой квадрат. Мы можем параметризовать два оставшихся угла, используя компоненты первых двух. В приведенном выше примере мы выражаем
P2 и
P4 с точки зрения
P1 = (x1,y1) и
P3 = (x3,y3). Если вам нужна визуализация геометрической интуиции, лежащей в основе параметризации квадрата, вы можете поиграть с интерактивной версией .
P2 = (x2,y2) = ( (x1+x3-y3+y1)/2 , (y1+y3-x1+x3)/2 )
P4 = (x4,y4) = ( (x1+x3+y3-y1)/2 , (y1+y3+x1-x3)/2 )
Замена на
x2,x4,y2,y4 Значит это
f(x1,...,y4) можно переписать на:
f(x1,x3,y1,y3) = (x1-ax)^2+(y1-ay)^2 + ((x1+x3-y3+y1)/2-bx)^2+((y1+y3-x1+x3)/2-by)^2 +
(x3-cx)^2+(y3-cy)^2 + ((x1+x3+y3-y1)/2-dx)^2+((y1+y3+x1-x3)/2-dy)^2
функция, которая зависит только от
x1,x3,y1,y3. Чтобы найти минимум полученной функции, мы затем устанавливаем частные производные от
f(x1,x3,y1,y3)равно нулю. Это следующие:
df/dx1 = 4x1-dy-dx+by-bx-2a = 0 --> x1 = ( dy+dx-by+bx+2a)/4
df/dx3 = 4x3+dy-dx-by-bx-2e = 0 --> x3 = (-dy+dx+by+bx+2e)/4
df/dy1 = 4y1-dy+dx-by-bx-2b = 0 --> y1 = ( dy-dx+by+bx+2b)/4
df/dy3 = 4y3-dy-dx-2f-by+bx = 0 --> y3 = ( dy+dx+2f+by-bx)/4
Вы можете увидеть, к чему все идет, поскольку простая перестановка терминов приводит к окончательному решению.