Байесовская скользящая пуассоновская регрессия в зазубринах (через R2jags)
Эта проблема
У меня есть небольшой набор данных (N=100). Мне нужно запустить регрессию Пуассона, но исключая одно наблюдение за раз (следовательно, регрессию Роллинг- Пуассона).
В уравнении есть несколько предикторов, но я забочусь об одном (назовите его bx). Моя идея состоит в том, чтобы увидеть, как bx варьируется между 100 моделями. Затем я хотел бы построить эти 100 точечных оценок с размерами эффекта на оси Y и номером модели на оси X.
В итоге мне нужно следующее:
Запустите Регулярную регрессию Пуассона в JAGS (через R2jags).
Получив оценки, подготовьте их.
Обратите внимание, что моя модель Пуассона в JAGS работает нормально (ниже приведен пример игрушки моей модели / данных). Тем не менее, я не смог реализовать версию "Роллинг".
Автономный пример
# clear R
rm(list=ls())
cat("\014")
# load libraries
if (!require("pacman")) install.packages("pacman"); library(pacman)
p_load(R2jags)
# Toy Data
N <- 100
x <- rnorm(n=N) # standard Normal predictor
y <- rpois(n=N, lambda = 1) # Poisson DV
# model
model <- function() {
## Likelihood
for(i in 1:N){
y[i] ~ dpois(lambda[i])
log(lambda[i]) <-
mu + # intercept
b.x*x[i]
}
## Priors
mu ~ dnorm(0, 0.01) ## intercept
b.x ~ dnorm(0, 0.01)
}
# list elements
data.list <- list(N = N, y = y, x = x)
# run model
model.fit <- jags(
data=data.list,
inits=NULL,
parameters.to.save = c("b.x"),
n.chains = 1,
n.iter = 20,
n.burnin = 2,
model.file=model,
progress.bar = "none")
Хорошо. Это модель. В model.fit есть bx, коэффициент я должен получить в 100 раз. С моим текущим кодом я могу получить его только один раз с полным набором данных. Однако мне нужно получить его во второй раз, исключив первый ряд df, а затем в третий раз, но исключив второй ряд df, и так далее, и так далее. И затем, нанесите на карту все эти BX.
Теперь, просто для примера, я создам простую таблицу, чтобы показать, что мне нужен первый элемент (коэффициент bx).
## I sourced this function below from https://raw.githubusercontent.com/jkarreth/JKmisc/master/mcmctab.R
# Function to Create Table
mcmctab <- function(sims, ci = .8, digits = 2){
require(coda)
if(class(sims) == "jags" | class(sims) == "rjags"){
sims <- as.matrix(as.mcmc(sims))
}
if(class(sims) == "bugs"){
sims <- sims$sims.matrix
}
if(class(sims) == "mcmc"){
sims <- as.matrix(sims)
}
if(class(sims) == "mcmc.list"){
sims <- as.matrix(sims)
}
if(class(sims) == "stanfit"){
stan_sims <- rstan::As.mcmc.list(sims)
sims <- as.matrix(stan_sims)
}
dat <- t(sims)
mcmctab <- apply(dat, 1,
function(x) c(Mean = round(mean(x), digits = digits), # Posterior mean
SD = round(sd(x), digits = 3), # Posterior SD
Lower = as.numeric(
round(quantile(x, probs = c((1 - ci) / 2)),
digits = digits)), # Lower CI of posterior
Upper = as.numeric(
round(quantile(x, probs = c((1 + ci) / 2)),
digits = digits)), # Upper CI of posterior
Pr. = round(
ifelse(mean(x) > 0, length(x[x > 0]) / length(x),
length(x[x < 0]) / length(x)),
digits = digits) # Probability of posterior >/< 0
))
return(t(mcmctab))
}
# this is the coefficient I need, but with different data frames.
mcmctab(model.fit)[1,1]
Извините, я даже не могу предоставить здесь попытку решения. Большое спасибо заранее.
2 ответа
# clear R
rm(list=ls())
# load libraries
library(R2jags)
# Toy Data
set.seed(123) # set RNG seed for reproducibility
N <- 100
x <- rnorm(n=N) # standard Normal predictor
y <- rpois(n=N, lambda = 1) # Poisson DV
# model
model <- function() {
## Likelihood
for(i in 1:N){
y[i] ~ dpois(lambda[i])
log(lambda[i]) <-
mu + # intercept
b.x*x[i]
}
## Priors
mu ~ dnorm(0, 0.01) ## intercept
b.x ~ dnorm(0, 0.01)
}
# list elements
data.list <- list() # create empty list to fill in next line
# fill list with one data set for each step, with one row excluded per step
for(i in 1:100){
data.list[[i]] <- list(N = 99, y = y[-i], x = x[-i])
}
# Starting value for reproducibility
model.inits <- function(){
list("b.x" = 0)
}
# run model
model.fit <- list() # again, create empty list first
for(i in 1:100){ # use loop here to fit one model per data set
model.fit[[i]] <- jags(
data=data.list[[i]],
inits=NULL,
parameters.to.save = c("b.x"),
n.chains = 1,
n.iter = 20,
n.burnin = 2,
model.file=model,
progress.bar = "none")
}
# helper function for output
devtools::source_url("https://raw.githubusercontent.com/jkarreth/JKmisc/master/mcmctab.R")
# create empty data frame to be filled with estimation results per data set
tab <- data.frame(index = c(1:100), b = rep(NA, 100), lower = rep(NA, 100), upper = rep(NA, 100))
# fill with estimates, using mcmctab to extract mean & lower & upper CIs
for(i in 1:100){
tab[i, 2] <- mcmctab(model.fit[[i]])[1, 1]
tab[i, 3] <- mcmctab(model.fit[[i]])[1, 3]
tab[i, 4] <- mcmctab(model.fit[[i]])[1, 4]
}
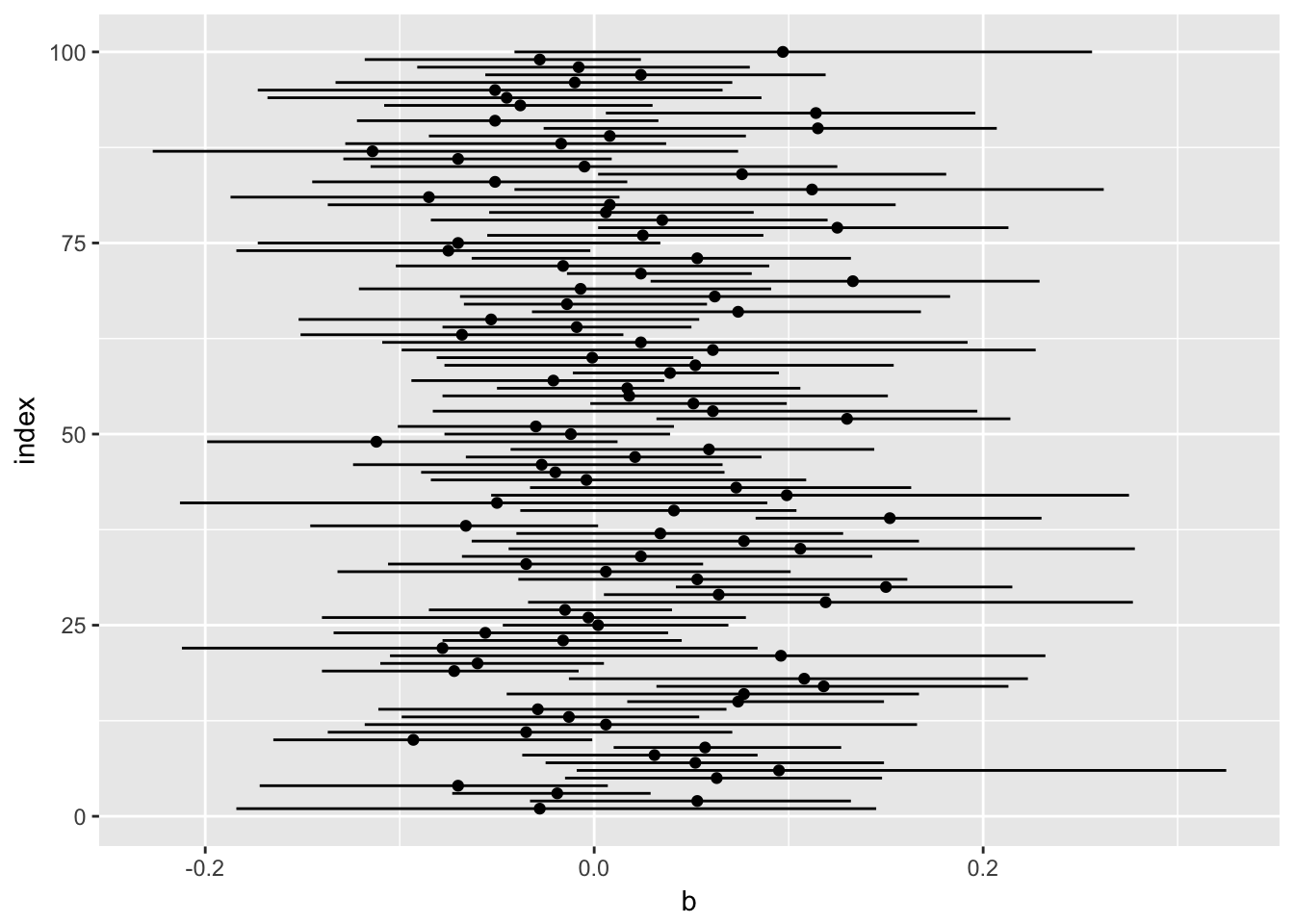
# plot results
library(ggplot2)
p <- ggplot(data = tab, aes(x = b, y = index)) + geom_point() + geom_segment(aes(x = lower, xend = upper, yend = index))
p
Я благодарю Йоханнеса Каррета за любезный ответ на этот замечательный вопрос.
Используйте цикл for или один из apply Члены семьи исключают одно наблюдение за раз:
sims <- lapply(1:100, function(i) {
data.list <- list(N = N - 1, y = y[-i], x = x[-i])
# run model
model.fit <- jags(
data=data.list,
inits=NULL,
parameters.to.save = c("b.x"),
n.chains = 1,
n.iter = 20,
n.burnin = 2,
model.file=model,
progress.bar = "none")
return(model.fit)
})
Затем вы можете извлечь интересующее вас количество, просматривая вывод:
sapply(sims, function(x) x$BUGSoutput$mean$b.x)
# [1] -0.018966261 -0.053383364 -0.030193649 -0.097046841 -0.026258934
# [6] -0.005486296 0.084811315 -0.047736880 0.142379194 -0.026583145
# <snip>